最近在刷leetcode题目,积累了一些提醒以及用c++STL刷题经验,这里记录一下
题型
数组与字符串
数组是存放在连续内存空间上的相同类型数据的集合。数组可以方便的通过下标索引的方式获取到下标对应的数据
- 数组下标都是从0开始的。
- 数组内存空间的地址是连续的
正是因为数组在内存空间的地址是连续的，所以我们在删除或者增添元素的时候，就难免要移动其他元素的地址。例如删除下标为3的元素，需要对下标为3的元素后面的所有元素都要做移动操作
最大子数组和
给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。子数组是数组中的一个连续部分。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
int maxSubArray(vector<int>& nums) {
// 贪心或者动态规划
int result{numeric_limits<int>::min()};
int count{};
for(int i = 0;i<nums.size();++i) {
count +=nums[i];
if(count>result) {
result = count;
}
if(count<=0) {
count = 0;
}
}
return result;
}
};1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
int maxSubArray(vector<int>& nums) {
// 贪心或者动态规划
int pre{}, maxAns{nums[0]};
for (auto n : nums) {
pre = max(pre,pre+n); // 记录最大值
maxAns = max(maxAns,pre);
}
return maxAns;
}
};
轮转数组
给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。
可以使用额外的数组来将每个元素放至正确的位置。用 n 表示数组的长度，我们遍历原数组，将原数组下标为 i 的元素放至新数组下标为 (i+k)modn 的位置，最后将新数组拷贝至原数组即可。1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
void rotate(vector<int>& nums, int k) {
int sz = nums.size();
vector<int> r(sz);
for(int i = 0;i<sz;++i) {
r[(i+k)%sz] = nums[i];
}
nums = r;
}
};
还可以通过旋转数组的方法1
2
3
4
5
6
7
8
9
10 class Solution {
public:
void rotate(vector<int>& nums, int k) {
int sz = nums.size();
k = k%sz;
reverse(nums.begin(),nums.end());
reverse(nums.begin(),nums.begin()+k);
reverse(nums.begin()+k,nums.end());
}
};
在使用vector和string的方法以及stl包含的方法时,比如find,insert,erase,substr方法的参数类型与返回值类型. 有的支持迭代器,有的重载了索引类型等
哈希
一般来说哈希表都是用来快速判断一个元素是否出现集合里。
对于哈希表，要知道哈希函数和哈希碰撞在哈希表中的作用。
哈希函数是把传入的key映射到符号表的索引上。
哈希碰撞处理有多个key映射到相同索引上时的情景，处理碰撞的普遍方式是拉链法和线性探测法。
常见的三种哈希结构:数组,set,map. 注意在不同场景使用不同的数据结构.
| 集合 | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
|---|---|---|---|---|---|---|
| std::set | 红黑树 | 有序 | 否 | 否 | O(log n) | O(log n) |
| std::multiset | 红黑树 | 有序 | 是 | 否 | O(logn) | O(logn) |
| std::unordered_set | 哈希表 | 无序 | 否 | 否 | O(1) | O(1) |
| 映射 | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
|---|---|---|---|---|---|---|
| std::map | 红黑树 | key有序 | key不可重复 | key不可修改 | O(logn) | O(logn) |
| std::multimap | 红黑树 | key有序 | key可重复 | key不可修改 | O(log n) | O(log n) |
| std::unordered_map | 哈希表 | key无序 | key不可重复 | key不可修改 | O(1) | O(1) |
set 和 map 是基于红黑树实现的，能够自动对元素进行排序。
插入、删除和查找
| 方法 | 描述 | set / map | unordered_set / unordered_map |
|---|---|---|---|
insert() | 插入元素 | 插入单个元素或范围内的元素，时间复杂度 O(logn) | 插入单个元素或范围内的元素，平均时间复杂度 O(1) |
erase() | 删除元素 | 删除单个元素、指定迭代器或范围内的元素，时间复杂度 O(logn) | 删除单个元素或范围内的元素，平均时间复杂度 O(1) |
count() | 计算元素数量 | 返回某个键在容器中出现的次数（set/map 中只会是 0 或 1），时间复杂度 O(logn) | 返回某个键在容器中出现的次数，平均时间复杂度 O(1) |
find() | 查找元素 | 查找元素，并返回指向该元素的迭代器，如果找不到则返回 end()，时间复杂度 O(logn) | 查找元素，并返回指向该元素的迭代器，如果找不到则返回 end()，平均时间复杂度 O(1) |
有效的字母异位词
给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的 字母异位词
字母异位词是通过重新排列不同单词或短语的字母而形成的单词或短语，并使用所有原字母一次。
最长连续序列
给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。请你设计并实现时间复杂度为 O(n) 的算法解决此问题
首先，将所有数组元素放入一个哈希表中，这样我们就可以在 O(1) 的时间复杂度内判断一个数字是否存在。然后，我们遍历数组中的每一个数字，并以这个数字为起点，向后和向前查找连续的数字。为了确保每个连续序列只被计算一次，我们只从一个序列的起始数字开始查找。一个数字 x 是一个连续序列的起始数字的条件是：x - 1 不存在于哈希表中。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
public:
int longestConsecutive(vector<int>& nums) {
// 插入到哈希集合中
unordered_set<int> uset; // 存储值以及以其结尾的对应连续最长序列长度
for (auto n : nums) {
uset.insert(n);
}
int longStreak{};
// 遍历nums,从set中找到这个包含nums的连续序列的最小值
for (const int& n : uset) {
if (uset.count(n - 1)) {
// n不是连续序列最小值
continue;
}
// 找到连续序列的第一个值
// n是序列最小值
int cur{1};
int curNum = n+1;
while (uset.count(curNum)) {
cur++;
curNum++;
}
longStreak = max(longStreak, cur);
}
return longStreak;
}
};
快乐数
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为：
- 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1，那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ；不是，则返回 false 。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
bool isHappy(int n) {
// 检查环形链
// 如果得到相同的值 就是检测到环形链
unordered_set<int> sets;
while (!sets.count(n) && n!=1) {
sets.insert(n);
int tmp = n;
n = 0;
while (tmp) {
n += (tmp % 10)*(tmp % 10);
tmp /= 10;
}
}
return n == 1;
}
};1
2
3
4
5
6
7
8
9
10int slow = n,fast = n;
while(fast!=1&&getSum(fast)!=1) {
// 如果存在环形链,则总会有slow == fast
slow = getSum(slow);
fast = getSum(getSum(fast));
if(slow == fast) {
return false;
}
}
return true;
四数相加II
给你四个整数数组 nums1、nums2、nums3 和 nums4 ，数组长度都是 n ，请你计算有多少个元组 (i, j, k, l) 能满足：
0 <= i, j, k, l < nnums1[i] + nums2[j] + nums3[k] + nums4[l] == 0
1 | int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) { |
赎金信
给你两个字符串：ransomNote 和 magazine ，判断 ransomNote 能不能由 magazine 里面的字符构成。如果可以，返回 true ；否则返回 false 。magazine 中的每个字符只能在 ransomNote 中使用一次。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
bool canConstruct(string ransomNote, string magazine) {
// 如果能由magazine字符串构成,表示
vector<int> cnt(26);
for (int i = 0; i < magazine.size(); ++i) {
cnt[magazine[i] - 'a']++;
}
for (int i = 0; i < ransomNote.size(); ++i) {
int c = ransomNote[i] - 'a';
if (cnt[c] > 0) {
// 大于0表示还有剩余字符
cnt[c]--;
} else {
return false;
}
}
return true;
}
};
直线上最多的点数
双指针与链表
虚拟头节点 链表的一大问题就是操作当前节点必须要找前一个节点才能操作。这就造成了，头结点的尴尬，因为头结点没有前一个节点了。每次对应头结点的情况都要单独处理，所以使用虚拟头结点的技巧，就可以解决这个问题
反转链表 删除倒数第n个节点 链表相交 环形链表
双指针主要用于遍历数组，两个指针指向不同的元素，从而协同完成任务。也可以延伸到多个数组的多个指针。若两个指针指向同一数组，遍历方向相同且不会相交，则也称为滑动窗口（两个指针包围的区域即为当前的窗口），经常用于区间搜索。
若两个指针指向同一数组，但是遍历方向相反，则可以用来进行搜索，待搜索的数组往往是排好序的。
在对链表进行操作时，一种常用的技巧是添加一个哑节点（dummy node），它的 next 指针指向链表的头节点。这样一来，我们就不需要对头节点进行特殊的判断了。
快慢指针 检查环
延迟节点
常见题型, 合并2,合并k,分解,环形链表,倒数k,重点,找交点.
删除链表元素
给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回 新的头节点 。
设置一个虚拟头结点在进行移除节点操作1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
if (head == nullptr) {
return nullptr;
}
ListNode* dummy = new ListNode(0, head);
ListNode* cur = dummy;
while (cur->next) {
if (cur->next->val == val) {
// 删除当前节点
ListNode* tmp = cur->next;
cur->next = cur->next->next;
delete tmp;
} else {
cur = cur->next;
}
}
return dummy->next;
}
};
反转链表
给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。
使用哑节点或者递归方式1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* prev = nullptr;
while (head) {
ListNode* head_next = head->next;
head->next = prev;
prev = head;
head = head_next;
}
return prev;
}
};
递归1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
ListNode* reverseList(ListNode* head,ListNode* prev=nullptr) {
if(head == nullptr) {
return prev;
}
ListNode* head_next = head->next;
head->next = prev;
return reverseList(head_next,head);;
}
};
删除链表倒数第n个节点
给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
// 延迟n步的节点
// 双指针和哑节点
// 哑节点
ListNode* dummy = new ListNode(0,head);
ListNode* first = head;
ListNode* second = dummy;
// 不首先遍历获得节点总数
for(int i = 0;i<n;++i) {
// 指向第n个节点
first = first->next; // first和second之间有n-1个节点
}
while(first) {
first = first->next;
second = second->next;
}
second->next = second->next->next;
return dummy->next;
}
};
环形链表
给你一个链表的头节点 head ，判断链表中是否有环。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39class Solution {
public:
bool hasCycle(ListNode *head) {
// 快慢指针
if(head == nullptr) {
return false;
}
ListNode* slowPtr = head,*fastPtr = head;
while(fastPtr && fastPtr->next!=nullptr) {
slowPtr = slowPtr->next;
fastPtr = fastPtr->next->next;
if(slowPtr == fastPtr) {
return true;
}
}
return false;
}
};
class Solution {
public:
bool hasCycle(ListNode *head) {
// 快慢指针
if(head == nullptr) {
return false;
}
ListNode* slowPtr = head,*fastPtr = head->next;
while(fastPtr!=slowPtr) {
if(fastPtr== nullptr || fastPtr->next == nullptr) {
return false;
}
slowPtr = slowPtr->next;
fastPtr = fastPtr->next->next;
}
return true;
}
};
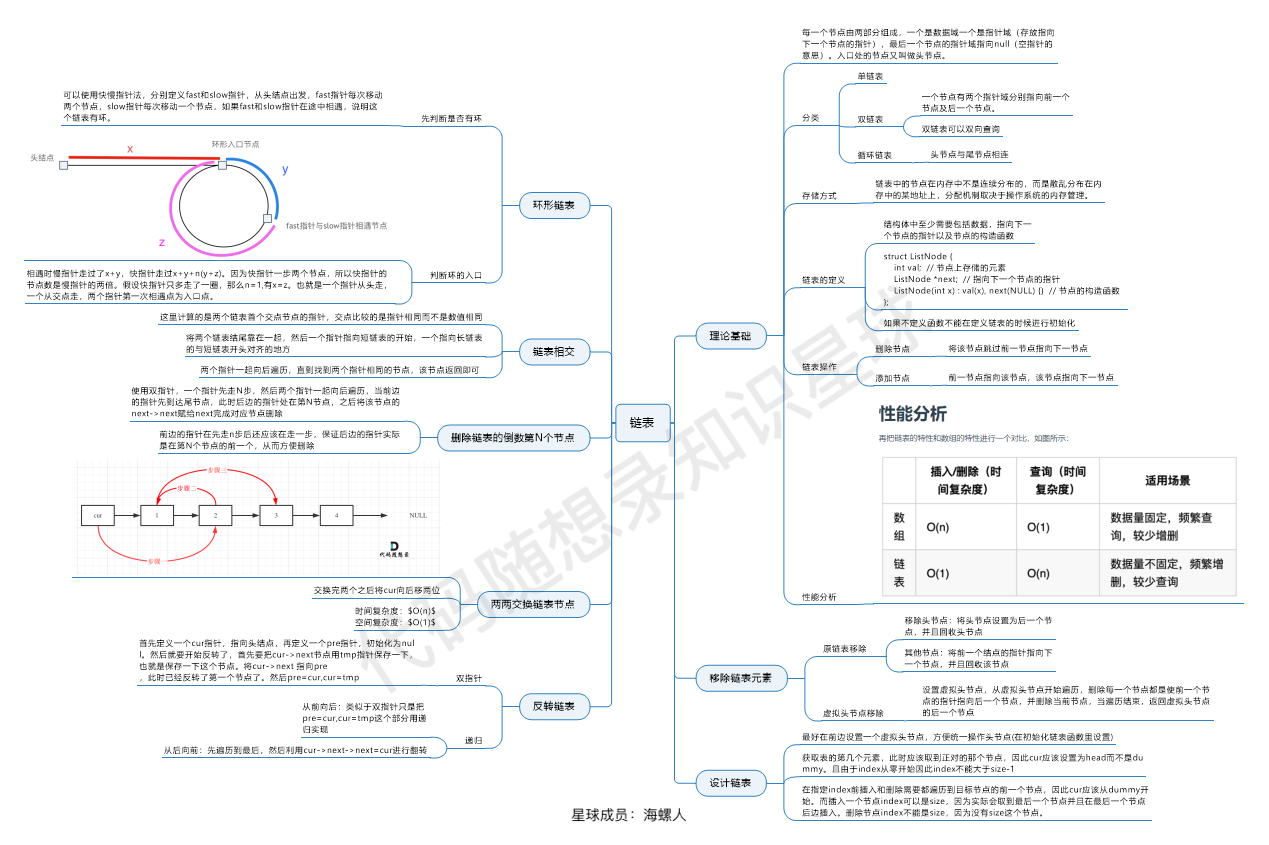
环形链表II
给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。
主要考察两知识点：
- 判断链表是否环
- 如果有环，如何找到这个环的入口
可以使用快慢指针法，分别定义 fast 和 slow 指针，从头结点出发，fast指针每次移动两个节点，slow指针每次移动一个节点，如果 fast 和 slow指针在途中相遇 ，说明这个链表有环。这是因为fast是走两步，slow是走一步，其实相对于slow来说，fast是一个节点一个节点的靠近slow的，所以fast一定可以和slow重合。从头结点出发一个指针，从相遇节点 也出发一个指针，这两个指针每次只走一个节点， 那么当这两个指针相遇的时候就是 环形入口的节点.
代码随想录1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
ListNode* detectCycle(ListNode* head) {
if (head == nullptr) {
return nullptr;
}
// 快慢指针 当两个指针相遇时
// ptr从head开始走直到ptr == slow
ListNode *slowPtr = head, *fastPtr = head;
while (fastPtr != nullptr) {
slowPtr = slowPtr->next;
if (fastPtr->next == nullptr) {
return nullptr;
}
fastPtr = fastPtr->next->next;
// 快慢指针在环上一点相遇
if (slowPtr == fastPtr) {
ListNode* cur = head;
while (slowPtr != cur) {
cur = cur->next;
slowPtr = slowPtr->next;
}
return cur;
}
}
return nullptr;
}
};
相交链表
给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。
只有当链表 headA 和 headB 都不为空时，两个链表才可能相交。因此首先判断链表 headA 和 headB 是否为空，如果其中至少有一个链表为空，则两个链表一定不相交，返回 null。
当链表 headA 和 headB 都不为空时，创建两个指针 pA 和 pB，初始时分别指向两个链表的头节点 headA 和 headB，然后将两个指针依次遍历两个链表的每个节点。具体做法如下：
每步操作需要同时更新指针 pA 和 pB。
如果指针 pA 不为空，则将指针 pA 移到下一个节点；如果指针 pB 不为空，则将指针 pB 移到下一个节点。
如果指针 pA 为空，则将指针 pA 移到链表 headB 的头节点；如果指针 pB 为空，则将指针 pB 移到链表 headA 的头节点。
当指针 pA 和 pB 指向同一个节点或者都为空时，返回它们指向的节点或者 null。
交换链表中两两节点
给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。
建议使用虚拟头结点，这样会方便很多，要不然每次针对头结点（没有前一个指针指向头结点），还要单独处理。
如果要删除倒数第n个节点，让fast移动n步，然后让fast和slow同时移动，直到fast指向链表末尾。删掉slow所指向的节点就可以了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
public:
ListNode* swapPairs(ListNode* head) {
if (head == nullptr) {
return nullptr;
}
ListNode* dummy = new ListNode(0, head);
ListNode* cur = head;
ListNode* prev = dummy;
while (cur && cur->next) {
// cur和cur->next为要交换的一组
// prev指向第二个节点
ListNode* node1 = cur;
ListNode* node2 = cur->next;
// 上一组的节点指向第二个节点
prev->next = node2;
// node1指向下一个几点
node1->next = node2->next;
// node2指向node1
node2->next = node1;
// 移动prev和cur
prev = node1;
cur = node1->next;
}
return dummy->next;
}
};
回文链表
快慢指针+反向链表
k个一反转
给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。
k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。
你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
// 链表节点定义
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
if (!head || k == 1) {
return head;
}
ListNode* dummy = new ListNode(0);
dummy->next = head;
ListNode* pre = dummy; // pre 指向待翻转子链表的前一个节点
ListNode* end = dummy; // end 指向待翻转子链表的最后一个节点
while (end->next != nullptr) {
// 找到 end 节点，即第 k 个节点
for (int i = 0; i < k && end != nullptr; ++i) {
end = end->next;
}
if (end == nullptr) {
break; // 剩余节点不足 k 个，结束循环
}
ListNode* start = pre->next; // start 指向待翻转子链表的第一个节点
ListNode* nextGroup = end->next; // nextGroup 指向下一个子链表的头节点
// 断开连接，准备翻转
end->next = nullptr;
// 翻转子链表
pre->next = reverseList(start);
// 连接翻转后的子链表
start->next = nextGroup;
// 移动指针，为下一轮循环做准备
pre = start;
end = pre;
}
return dummy->next;
}
private:
// 标准的链表翻转函数
ListNode* reverseList(ListNode* head) {
ListNode* pre = nullptr;
ListNode* curr = head;
while (curr != nullptr) {
ListNode* nextTemp = curr->next;
curr->next = pre;
pre = curr;
curr = nextTemp;
}
return pre;
}
};
双指针与数组
数组题型 二分法 双指针 滑动窗口 前缀和 模拟行为 贪心
四数相加
1 | class Solution { |
移除元素
给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。
假设 nums 中不等于 val 的元素数量为 k，要通过此题，您需要执行以下操作：
- 更改
nums数组，使nums的前k个元素包含不等于val的元素。nums的其余元素和nums的大小并不重要。 - 返回
k。
双指针法（快慢指针法）： 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
定义快慢指针
- 快指针：寻找新数组的元素 ，新数组就是不含有目标元素的数组
- 慢指针：指向更新 新数组下标的位置
双指针法（快慢指针法）在数组和链表的操作中是非常常见的，很多考察数组、链表、字符串等操作的面试题，都使用双指针法1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int removeElement(vector<int>& nums, int val) {
// 双指针
// 确定指针含义
// 将不等于val的值移动到开头
// int i 写入指针 指向即将写入的位置
// int j 读指针 读取值 读到不等于val的值进行写入
int i{};
int sz = nums.size();
for(int j = 0;j<sz;j++) {
if(nums[j] !=val) {
nums[i++] = nums[j];//写入值
}
// 如果等于val跳过
}
return i;
}
};
有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
// nums本身有序 绝对值是从大->小->大
int i = 0, j = nums.size() - 1;
int sz = nums.size();
vector<int> r(sz);
int k = sz-1;
while (i <= j) {
int t1 = nums[i] * nums[i];
int t2 = nums[j] * nums[j];
if ( t1>=t2 ) {
r[k--] = t1;
i++;
} else {
r[k--] = t2;
j--;
}
}
return r;
}
};
长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int min_len{numeric_limits<int>::max()};
long long pre{};
int i{};
// 双指针 j指向要包含的数据[i,j]
for(int j = 0;j<nums.size();j++){
pre+=nums[j];
while(pre>=target) {
min_len = min(min_len,j-i+1);
pre -= nums[i];
i++;
}
}
return min_len == numeric_limits<int>::max()?0:min_len;
}
};
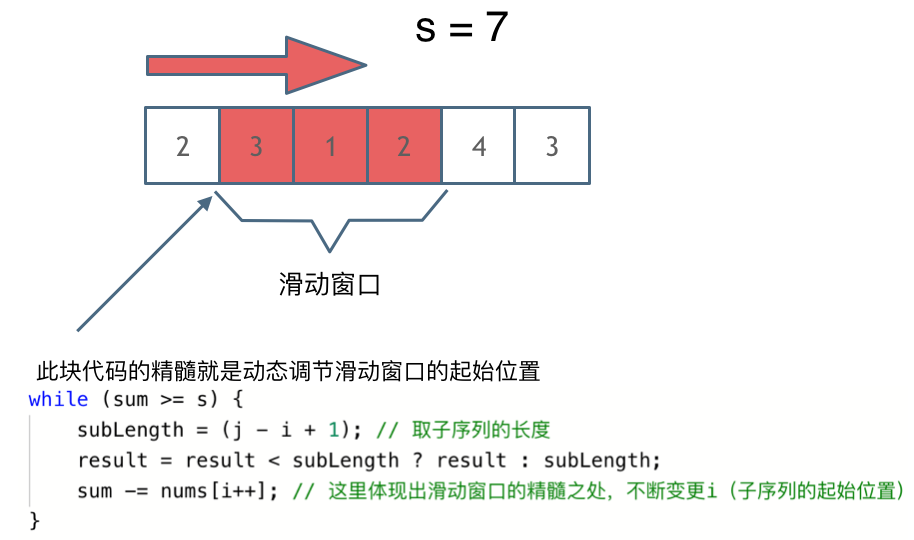
滑动窗口需要确定:窗口内是什么 什么时候移动窗口起始位置 什么时候移动窗口结束位置
每一个元素被操作的次数，每个元素在滑动窗后进来操作一次，出去操作一次，每个元素都是被操作两次，所以时间复杂度是 2 × n 也就是O(n)
滑动窗口。
- 暴力解法时间复杂度：O(n^2)
- 滑动窗口时间复杂度：O(n)
本题中，主要要理解滑动窗口如何移动 窗口起始位置，达到动态更新窗口大小的，从而得出长度最小的符合条件的长度。 滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。
螺旋矩阵
给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
array<pair<int, int>, 4> dirs{{{0, 1}, {1, 0}, {0, -1}, {-1, 0}}};
vector<vector<int>> r(n, vector<int>(n, 0));
int x{}, y{};
int dirIndex{};
for (int i = 1; i <= n * n; ++i) {
r[x][y] = i;
int nx = x + dirs[dirIndex].first;
int ny = y + dirs[dirIndex].second;
if (nx >= n || nx < 0 || ny >= n || ny < 0 || r[nx][ny] != 0) {
// 超出边界或者遇到已经填充的值
dirIndex = (dirIndex + 1) % 4;
nx = x + dirs[dirIndex].first;
ny = y + dirs[dirIndex].second;
}
x = nx;
y = ny;
}
return r;
}
};
区间和
给定一个整数数组 Array，请计算该数组在每个指定区间内元素的总和。
前缀和,前缀和的思想是重复利用计算过的子数组之和，从而降低区间查询需要累加计算的次数。
前缀和 在涉及计算区间和的问题时非常有用,想统计在vec数组上 下标 2 到下标 5 之间的累加和，就用 p[5] - p[1] 就可以。 注意计算区间和时的两端索引
最小覆盖字串
给定两个字符串 s 和 t 。返回 s 中包含 t 的所有字符的最短子字符串。如果 s 中不存在符合条件的子字符串，则返回空字符串 "" 。
如果 s 中存在多个符合条件的子字符串，返回任意一个。
注意： 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41class Solution {
public:
string minWindow(string s, string t) {
// 滑动窗口
vector<int> freq(256, 0);
vector<bool> exist(256, false);
for (auto ch : t) {
freq[ch]++;
exist[ch] = true;
}
int minLen{numeric_limits<int>::max()};
int min_l{numeric_limits<int>::max()};
int i{}; // 双指针 表示起始位置和截止位置
int sz = s.size();
int szt = t.size();
int counts{};
for (int j = 0; j < sz; j++) {
char ch = s[j];
if (!exist[ch]) {
continue;
}
freq[ch]--;
if (freq[ch] >= 0) {
counts++;
}
while (counts == szt) {
// 当窗口中包含了所有t字符 更新开始位置
if (minLen > j - i + 1) {
minLen = j - i + 1;
min_l = i;
}
if (exist[s[i]] && ++freq[s[i]] > 0) {
counts--;
}
i++;
}
}
return minLen == numeric_limits<int>::max() ? ""
: s.substr(min_l, minLen);
}
};
除自身以外的数组的乘积
给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法，且在 O(n) 时间复杂度内完成此题。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int length = nums.size();
vector<int> answer(length);
// answer[i] 表示索引 i 左侧所有元素的乘积
// 因为索引为 '0' 的元素左侧没有元素， 所以 answer[0] = 1
answer[0] = 1;
for (int i = 1; i < length; i++) {
answer[i] = nums[i - 1] * answer[i - 1];
}
// R 为右侧所有元素的乘积
// 刚开始右边没有元素，所以 R = 1
int R = 1;
for (int i = length - 1; i >= 0; i--) {
// 对于索引 i，左边的乘积为 answer[i]，右边的乘积为 R
answer[i] = answer[i] * R;
// R 需要包含右边所有的乘积，所以计算下一个结果时需要将当前值乘到 R 上
R *= nums[i];
}
return answer;
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
// 前缀 乘积
int sz = nums.size();
vector<int> r(sz, 1);
r[0] = 1;
for (int i = 1; i < sz; i++) {
r[i] = r[i-1]*nums[i-1];
}
// 利用输出数组
int cur{1};
for (int i = sz-1; i >=0; --i) {
r[i] = r[i] *cur;
cur*=nums[i];
}
return r;
}
};
参考:代码随想录
字符串
反转字符串
编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题1
2
3
4
5
6
7
8class Solution {
public:
void reverseString(vector<char>& s) {
for(int i =0,j = s.size()-1;i<s.size()/2;i++,j--) {
swap(s[i],s[j]);
}
}
};
反转字符串II
给定一个字符串 s 和一个整数 k，从字符串开头算起，每计数至 2k 个字符，就反转这 2k 字符中的前 k 个字符。
- 如果剩余字符少于
k个，则将剩余字符全部反转。 - 如果剩余字符小于
2k但大于或等于k个，则反转前k个字符，其余字符保持原样。
模拟,在遍历字符串的过程中，只要让 i += (2 k)，i 每次移动 2 k 就可以了，然后判断是否需要有反转的区间。
因为要找的也就是每2 k 区间的起点，这样写，程序会高效很多。所以当需要*固定规律一段一段去处理字符串的时候，要想想在for循环的表达式上做做文章。
1 | class Solution { |
反转字符串中的单词
给你一个字符串 s ，请你反转字符串中 单词 的顺序。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
注意：输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中，单词间应当仅用单个空格分隔，且不包含任何额外的空格。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
public:
string reverseWords(string s) {
// 先将整个字符串反转
reverse(s.begin(), s.end());
int sz = s.size();
int idx{};
string result;
for (int start = 0; start < sz; start++) {
if (s[start] != ' ') {
// 移除元素 移除空格 不为空格时
if (idx != 0) {
s[idx++] = ' ';
}
int end = start;
while (end < sz && s[end] != ' ') {
s[idx++] = s[end++];
}
reverse(s.begin() + idx - (end - start), s.begin() + idx);
// 更新start，去找下一个单词
start = end;
}
}
s.erase(idx); // 或者s.resize(idx);
return s;
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution {
public:
void removeDuplicateString(string& s) {
int sz = s.size();
int widx{};
for(int j = 0;j<sz;j++) {
if(s[j]!=' ') {
// 除非是开头 否则给字符串末尾添加空白符
if(widx!=0) {
s[widx++] = ' ';
}
//找到字符串写
while(j<sz && s[j]!=' ') {
s[widx++] = s[j++];
}
}
}
s.resize(widx);
}
string reverseWords(string s) {
// 先将整个字符串反转
removeDuplicateString(s);
reverse(s.begin(), s.end());
int sz = s.size();
int startPos{};
for(int j = 0;j<=sz;j++) {
if(j == sz || s[j] == ' ') {
//找到一个字符串结尾
reverse(s.begin()+startPos,s.begin()+j);
startPos = j+1;
}
}
return s;
}
};
旋转字符串
给定两个字符串, s 和 goal。如果在若干次旋转操作之后，s 能变成 goal ，那么返回 true 。
s 的 旋转操作 就是将 s 最左边的字符移动到最右边。
- 例如, 若
s = 'abcde'，在旋转一次之后结果就是'bcdea'
1 | class Solution { |
如果 s 和 goal 的长度不一样，那么无论怎么旋转，s 都不能得到 goal，返回 false。字符串 s+s 包含了所有 s 可以通过旋转操作得到的字符串，只需要检查 goal 是否为 s+s 的子字符串即可1
2
3
4
5
6
7
8
9class Solution {
public:
bool rotateString(string s, string goal) {
if(s.size()!=goal.size()) {
return false;
}
return (s+s).find(goal)!=string::npos;
}
};
右旋字符串
字符串的右旋转操作是把字符串尾部的若干个字符转移到字符串的前面。给定一个字符串 s 和一个正整数 k，请编写一个函数，将字符串中的后面 k 个字符移到字符串的前面，实现字符串的右旋转操作。
使用整体反转+局部反转就可以实现反转单词顺序的目的。需要将字符串右移n位，字符串相当于分成了两个部分，如果n为2，符串相当于分成了两个部分，右移n位， 就是将第二段放在前面，第一段放在后面，先不考虑里面字符的顺序，是不是整体倒叙不就行了，此时第一段和第二段的顺序是我们想要的，但里面的字符位置被我们倒叙，那么此时我们在把 第一段和第二段里面的字符再倒叙一把，这样字符顺序不就正确了，其实，思路就是 通过 整体倒叙，把两段子串顺序颠倒，两个段子串里的的字符在倒叙一把，负负得正，这样就不影响子串里面字符的顺序了。
整体代码如下：1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34// 版本一
using namespace std;
int main() {
int n;
string s;
cin >> n;
cin >> s;
int len = s.size(); //获取长度
reverse(s.begin(), s.end()); // 整体反转
reverse(s.begin(), s.begin() + n); // 先反转前一段，长度n
reverse(s.begin() + n, s.end()); // 再反转后一段
cout << s << endl;
}
// 版本二
using namespace std;
int main() {
int n;
string s;
cin >> n;
cin >> s;
int len = s.size(); //获取长度
reverse(s.begin(), s.begin() + len - n); // 先反转前一段，长度len-n ，注意这里是和版本一的区别
reverse(s.begin() + len - n, s.end()); // 再反转后一段
reverse(s.begin(), s.end()); // 整体反转
cout << s << endl;
}
字符串匹配
实现 strStr() 函数。
给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回 -1。
示例 1: 输入: haystack = “hello”, needle = “ll” 输出: 2
示例 2: 输入: haystack = “aaaaa”, needle = “bba” 输出: -1
KMP（Knuth-Morris-Pratt）算法是一种用于字符串匹配的高效算法，它在主字符串中查找一个模式字符串的出现位置。KMP 算法的核心思想是，在匹配过程中，当发生不匹配时，它能利用模式字符串自身已经匹配过的前缀和后缀信息，来避免回溯主字符串的指针。
KMP 算法主要分为两步：
- 预处理（构建
next数组）：- 遍历模式字符串
pattern，计算出其每个位置的最长相等前缀和后缀的长度，构建next数组。 - 这一步的时间复杂度是 O(m)，其中 m 是模式字符串的长度。
- 遍历模式字符串
- 匹配过程：
- 使用两个指针，一个指向
text（i），一个指向pattern（j）。 - 如果
text[i]和pattern[j]匹配，两个指针都向右移动。 - 如果不匹配，根据
next数组的值，将j指针移动到next[j-1]的位置，然后继续比较。主字符串的指针i不变。 - 如果
j回到了 -1（或 0），表示没有可以利用的前后缀，i向前移动一位，j从头开始。 - 当
j等于模式字符串的长度时，表示找到了一个匹配，记录匹配位置，并继续寻找下一个匹配。 - 这一步的时间复杂度是 O(n)，其中 n 是主字符串的长度
- 使用两个指针，一个指向
核心逻辑：next 数组告诉我们，当在 j 处发生不匹配时，pattern 的前 j 个字符中，有 next[j-1] 个字符的前缀和后缀是完全相同的。因此，我们可以将模式串的 j 指针移动到 next[j-1]，从而利用这部分已匹配的信息，避免重复比较1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36class Solution {
public:
int strStr(string haystack, string needle) {
// kmp 字符串匹配
int sz1 = haystack.size();
int sz2 = needle.size();
// 1.构建next数组 最长相同前后缀长度
vector<int> next(sz2,-1);
int j = -1; // 前缀
// i是后缀
for(int i = 1;i<sz2;++i) {
// 如果前后缀不同
while(j>-1 && needle[j+1]!=needle[i]) {
j = next[j];
}
if(needle[j+1] == needle[i]) {
j++;
}
next[i] = j;
}
// 2. 利用next数组进行匹配
j = -1;
for(int i=0;i<sz1;i++) {
while(j>-1&&haystack[i]!=needle[j+1]) {
j = next[j];
}
if(needle[j+1] == haystack[i]) {
j++;
}
if(j == sz2-1) {
return i-sz2+1;
}
}
return -1;
}
};
重复的字符串
给定一个非空的字符串 s ，检查是否可以通过由它的一个子串重复多次构成。
使用暴力解法,因子这个重复字串肯定是从头开始,设置结束指针进行遍历
使用KMP算法,计算next数组后,因为:字符串s的最长相等前后缀不包含的子串是s最小重复子串1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
public:
// 字符串匹配
bool repeatedSubstringPattern(string s) {
// 1. 构造next数组
int sz = s.size();
int j = -1;
vector<int> next(sz, -1);
for (int i = 1; i < sz; ++i) {
while (j >= 0 && s[j + 1] != s[i]) {
// 如果不匹配
j = next[j];
}
if (s[j + 1] == s[i]) {
j++;
}
next[i] = j;
}
// next[sz-1]+1 是最长相同前后缀长度
// 求大于-1的最小前缀长度看sz是否是其倍数
int t = sz - 1;
if (next[t] != -1 && sz%(sz-(next[t]+1)) == 0) {
return true;
}
return false;
}
};
还有一种需要证明的方法.判断字符串s是否由重复子串组成，只要两个s拼接在一起，里面还出现一个s的话，就说明是由重复子串组成(查找从第一个)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
bool repeatedSubstringPattern(string s) {
return (s + s).find(s, 1) != s.size();
}
};
class Solution {
public:
bool repeatedSubstringPattern(string s) {
string t = s + s;
t.erase(t.begin()); t.erase(t.end() - 1);
return t.find(s)!=string::npos;
}
};
双指针法是字符串处理的常客。
KMP算法是字符串查找最重要的算法,进行字符串匹配.
计数二进制子串
给定一个字符串 s，统计并返回具有相同数量 0 和 1 的非空（连续）子字符串的数量，并且这些子字符串中的所有 0 和所有 1 都是成组连续的。重复出现（不同位置）的子串也要统计它们出现的次数。
字符分组,要求我们找到满足特定条件的子字符串：
- 0和1的数量相等。
- 所有0是连续的，所有1也是连续的。
核心算法步骤
- 分组计数：遍历字符串，计算每个连续分组的长度，并存储在一个列表中。
- 例如，
"00110111"->[2, 2, 1, 3]。
- 例如，
- 配对求和：遍历分组长度列表，对于每对相邻的长度
a和b，将min(a, b)加到总计数中。- 例如，
[2, 2, 1, 3]。 min(2, 2) = 2min(2, 1) = 1min(1, 3) = 1- 总数 =
2 + 1 + 1 = 4。
- 例如，
1 | class Solution { |
1 | class Solution { |
同构字符串
给定两个字符串 s 和 t ，判断它们是否是同构的。
如果 s 中的字符可以按某种映射关系替换得到 t ，那么这两个字符串是同构的。
每个出现的字符都应当映射到另一个字符，同时不改变字符的顺序。不同字符不能映射到同一个字符上，相同字符只能映射到同一个字符上，字符可以映射到自己本身。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
bool isIsomorphic(string s, string t) {
if(s.size()!=t.size()) {
return false;
}
// 记录字符映射关系
// 相同位置的字符直接映射
int sz = s.size();
unordered_map<char,char> s2t;
unordered_map<char,char> t2s;
for(int i = 0;i<sz;++i) {
char x = s[i];
char y = t[i];
if((s2t.count(x) && s2t[x] != y) || (t2s.count(y) && t2s[y]!=x)) {
return false;
}
s2t[x] = y;
t2s[y] = x;
}
return true;
}
};
还可以使用数组,记录映射的字符的位置。记录两个字符串每个位置的字符第一次出现的位置，如果两个字符串中相同位置的字符与它们第一次出现的位置一样，那么这两个字符串同构。举例来说，对于“paper”和“title”，假设我们现在遍历到第三个字符“p”和“t”，发现它们第一次出现的位置都在第一个字符，则说明目前位置满足同构。同样的，我们可以用哈希表存储，也可以用一个长度为 128 的数组（ASCII 定义下字符的总数量）。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15if (s.length() != t.length()) {
return false;
}
// 记录字符串中相同位置字符映射关系与第一次出现时的映射关系是否相同
// 所以需要记录第一次出现的位置,根据这个位置看对应的关系是否一致
vector<int> s_init(128, 0), t_init(128, 0);
for (size_t i = 0; i < s.length(); ++i) {
if (s_init[s[i]] != t_init[t[i]]) {
// 如果出现的位置不同
return false;
}
// 出现的位置相同,有可能是第一次出现
s_init[s[i]] = t_init[t[i]] = i+1;
}
return true;
回文字符串
给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
回文字串总是以某个字符或两个字符的间隙为中心。我们可以遍历每一个可能的中心，然后向两侧扩展来寻找回文。
- 初始化计数器
count = 0。 - 遍历所有可能的中心点。总共有
2n-1个中心点： n个单字符中心：每个字符s[i]都可以作为中心。n-1个双字符间隙中心：每两个相邻字符s[i]和s[i+1]之间的间隙可以作为中心。
- 对于每个中心，使用两个指针
left和right向两边扩展。 - 当
left >= 0、right < n且s[left] == s[right]时，继续扩展，并增加计数器。 - 当
s[left] != s[right]时，停止扩展。 - 返回
count。
1 | int extendSubstrings(const string& s, int left, int right) { |
最长回文子串
移除无效的括号
给你一个由 '('、')' 和小写字母组成的字符串 s。
你需要从字符串中删除最少数目的 '(' 或者 ')' （可以删除任意位置的括号)，使得剩下的「括号字符串」有效。
请返回任意一个合法字符串。
有效「括号字符串」应当符合以下 任意一条 要求：
- 空字符串或只包含小写字母的字符串
- 可以被写作
AB（A连接B）的字符串，其中A和B都是有效「括号字符串」 - 可以被写作
(A)的字符串，其中A是一个有效的「括号字符串
最朴素的做法,使用新的字符串存储结果.先从左到右的遍历,遇到左括号,计数器+1,遇到右括号,看计数器是否大于0,如果等于0,表示右括号多了,则不加入结果,否则计数器-1加入结果. 然后从后向前遍历,遇到右括号,计数器+1,遇到左括号如果1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
using namespace std;
class Solution {
public:
string minRemoveToMakeValid(string s) {
int counts{};
// 双向遍历
// 从左到右
int sz = s.size();
string result;
for (int i = 0; i < sz; ++i) {
// 遇到( +1 遇到) -1,如果 小于0,不添加
char ch = s[i];
if (ch >= 'a' && ch <= 'z') {
result += ch;
continue;
}
if (ch == '(') {
counts++;
result += ch;
} else {
if (counts > 0) {
// 遇到多余右括号
counts--;
result += ch;
}
}
}
if (counts == 0) {
return result;
}
counts = 0;
string final_result{};
// 从右到左
for (int i = result.size() - 1; i >= 0; i--) {
// counts>0,从后往前遍历,遇到(括号
char ch = result[i];
if(ch >= 'a' && ch<='z') {
final_result+=ch;
continue;
}
if(ch == ')') {
counts++;
final_result+=ch;
}else {
if(counts>0) {
final_result+=ch;
counts--;
}
}
}
reverse(final_result.begin(),final_result.end());
return final_result;
}
};
如果不使用新字符串存储,可以通过符号标记,要删除的括号标记为#,使用原数组存储1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36// 记录左右括号的位置
int count = 0, n = s.length();
char to_delete = '#';
// 从前向后遍历,如果右括号比左括号多,标记那个右括号位置
for (char &c: s) {
if (c == '(') {
++count;
} else if (c == ')') {
if (count > 0) {
--count;
} else {
// 右括号比左括号多
// 将当前右括号位置标记
// 标记多出的右括号
c = to_delete;
}
}
}
// 从后向前遍历
// 删除多余的左括号
for (int i = n - 1; i >= 0; --i) {
if (count == 0) {
break;
}
if (s[i] == '(') {
// 多余的
s[i] = to_delete;
--count;
}
}
s.erase(remove(s.begin(), s.end(), to_delete),s.end());
return s;
// 将标记的位置通过erase(remove)删除
基本计算器
给你一个字符串表达式 s ，请你实现一个基本计算器来计算并返回它的值。
整数除法仅保留整数部分。
你可以假设给定的表达式总是有效的。所有中间结果将在 [-231, 231 - 1] 的范围内。
注意：不允许使用任何将字符串作为数学表达式计算的内置函数，比如 eval() 。
如果我们在字符串左边加上一个加号，可以证明其并不改变运算结果，且字符串可以分割成多个 < 一个运算符，一个数字 > 对子的形式；这样一来我们就可以从左往右处理了。由于乘除的优先级高于加减，因此我们需要使用一个中间变量来存储高优先度的运算结果。
此类型题也考察很多细节处理，如无运算符的情况，和多个空格的情况等等。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50class Solution {
public:
int parseNum(const string& s, int& i) {
int num{};
while (i < s.size() && isdigit(s[i])) {
num = 10 * num + (s[i++] - '0');
}
return num;
}
int calculate(string s) {
int sz = s.size();
char op = '+';
long localNum{}, result{};
int i{-1};
while (++i < sz) {
char ch = s[i];
if (ch == ' ') {
continue;
}
int num = parseNum(s, i);
switch (op) {
// op是上次的运算符
// 如果是+或-,result+=localNum,并且是+localNum设置为num,是-设置为-num
// *和/需要将上次的localNum进行运算
// 相当于
case '+':
result += localNum;
localNum = num;
break;
case '-':
result += localNum;
localNum = -num;
break;
case '*':
localNum *= num;
break;
case '/':
localNum /= num;
break;
}
while(i<sz && s[i] == ' ') {
i++;
}
if (i < sz) {
op = s[i];
}
}
return result + localNum;
}
};
贪心算法
顾名思义，贪心算法或贪心思想 (greedy algorithm) 采用贪心的策略，保证每次操作都是局部最优的，从而使最后得到的结果是全局最优的。
证明一道题能用贪心算法解决，有时远比用贪心算法解决该题更复杂。一般情况下，在简单操作后，具有明显的从局部到整体的递推关系，或者可以通过数学归纳法推测结果时，我们才会使用贪心算法。
贪心算法一般分为如下四步：
- 将问题分解为若干个子问题
- 找出适合的贪心策略
- 求解每一个子问题的最优解
- 将局部最优解堆叠成全局最优解
分发饼干
假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。
对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是满足尽可能多的孩子，并输出这个最大数值。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(g.begin(), g.end());
sort(s.begin(), s.end());
// 排序+双指针+贪心
int cnt{};
for (int i = 0, j = 0; i < g.size() && j < s.size(); j++) {
// 胃口和尺寸都递增,当胃口小于尺寸,尺寸指针idx移动,否则两者都移动
if (g[i] <= s[j]) {
// 尺寸更大
i++;
cnt++;
}
}
return cnt;
}
};
跳跃游戏
给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false
这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点.每次移动取最大跳跃步数（得到最大的覆盖范围），每移动一个单位，就更新最大覆盖范围.
贪心算法局部最优解：每次取最大跳跃步数（取最大覆盖范围），整体最优解：最后得到整体最大覆盖范围，看是否能到终点。
局部最优推出全局最优，找不出反例，试试贪心1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
bool canJump(vector<int>& nums) {
int cover = 0;
if (nums.size() == 1) return true; // 只有一个元素，就是能达到
for (int i = 0; i <= cover; i++) { // 注意这里是小于等于cover
cover = max(i + nums[i], cover);
if (cover >= nums.size() - 1) return true; // 说明可以覆盖到终点了
}
return false;
}
};
跳跃游戏II
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向后跳转的最大长度。换句话说，如果你在索引 i 处，你可以跳转到任意 (i + j) 处：
0 <= j <= nums[i]且i + j < n
返回到达 n - 1 的最小跳跃次数。测试用例保证可以到达 n - 1。
问题的目标是找到最小跳跃次数。我们可以从起点开始，一步步地计算出每一步能到达的最远位置。
这个贪心算法的核心是：在每一步中，我们都尽可能地跳到当前能到达的最远位置。
current_reach：当前这一步能跳到的最远位置，初始为 0。
farthest_reach：从起点到当前位置，所有可能跳跃路径中能达到的最远位置，初始为 0。
贪心的思路，局部最优：当前可移动距离尽可能多走，如果还没到终点，步数再加一。整体最优：一步尽可能多走，从而达到最少步数。
思路虽然是这样，但在写代码的时候还不能真的能跳多远就跳多远，那样就不知道下一步最远能跳到哪里了。所以真正解题的时候，要从覆盖范围出发，不管怎么跳，覆盖范围内一定是可以跳到的，以最小的步数增加覆盖范围，覆盖范围一旦覆盖了终点，得到的就是最少步数这里需要统计两个覆盖范围，当前这一步的最大覆盖和下一步最大覆盖。
如果移动下标达到了当前这一步的最大覆盖最远距离了，还没有到终点,那么就必须再走一步来增加覆盖范围，直到覆盖范围覆盖了终点。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int jump(vector<int>& nums) {
// 贪心 每步看能否到达n-1 如果不能选择最大值
int current_search{};
int farest_search{};
int steps{};
for(int j = 0;j<nums.size()-1;j++) {
farest_search = max(farest_search,j+nums[j]);
if(j == current_search) {
steps++;
current_search = farest_search;
if(current_search>=nums.size()-1) {
break;
}
}
}
return steps;
}
};
划分字母区间
给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。例如，字符串 "ababcc" 能够被分为 ["abab", "cc"]，但类似 ["aba", "bcc"] 或 ["ab", "ab", "cc"] 的划分是非法的。
注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。
返回一个表示每个字符串片段的长度的列表。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
vector<int> partitionLabels(string s) {
// 贪心算法选择
vector<int> cnt(26);
for (int i = 0; i < s.size(); i++) {
cnt[s[i] - 'a'] = i; // 记录最后一次出现的索引
}
int start_pos{}, end_pos{};
vector<int> r;
for (int i = 0; i < s.size(); i++) {
end_pos = max(end_pos, cnt[s[i] - 'a']);
if (i == end_pos) {
// 到达边界
r.emplace_back(end_pos - start_pos + 1);
start_pos = i + 1; // 更新分片起始点
}
}
return r;
}
};
摆动序列
如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 摆动序列 。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
- 例如，
[1, 7, 4, 9, 2, 5]是一个 摆动序列 ，因为差值(6, -3, 5, -7, 3)是正负交替出现的。 - 相反，
[1, 4, 7, 2, 5]和[1, 7, 4, 5, 5]不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。
给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度
可以使用贪心或者动态规划
贪心需要注意prev_diff==0时含义,只在diff(nums[i]-nums[i-1])不等于0时才可能变化,并且只需要在坡度摆动变化的时候，更新 prediff ，这样 prediff 在 单调区间有平坡的时候 就不会发生变化。
记录当前序列的上升下降趋势。每次加入一个新元素时，用新的上升下降趋势与之前对比，如果出现了「峰」或「谷」，答案加一，并更新当前序列的上升下降趋势。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
// 局部最优->全局最优
// 删除单调坡上的中间节点(不包括两边节点)
if (nums.size() == 1) {
return 1;
}
// 使用down,up记录
int prev_diff = nums[1] - nums[0];
int cnt{1};
cnt += prev_diff == 0 ? 0 : 1;
for (int i = 2; i < nums.size(); ++i) {
int diff = nums[i] - nums[i - 1];
if ((diff > 0 && prev_diff <= 0) || (prev_diff >= 0 && diff < 0)) {
cnt++;
prev_diff = diff;
}
}
return cnt;
}
};
局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值。整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列
实际操作上，其实连删除的操作都不用做，因为题目要求的是最长摆动子序列的长度，所以只需要统计数组的峰值数量就可以了（相当于是删除单一坡度上的节点，然后统计长度）这就是贪心所贪的地方，让峰值尽可能的保持峰值，然后删除单一坡度上的节点
在计算是否有峰值的时候，遍历的下标 i ，计算 prediff（nums[i] - nums[i-1]） 和 curdiff（nums[i+1] - nums[i]），如果prediff < 0 && curdiff > 0 或者 prediff > 0 && curdiff < 0 此时就有波动就需要统计。考虑上下坡中有平坡情况,删除左边三个值,也就是prev_diff=0但cur_dff不为0.所以记录峰值的条件应该是： (preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)，为什么这里允许 prediff == 0 就是为了这种情况.此外考虑单调坡平坡的情况,需要在这个坡度摆动变化的时候，更新 prediff，这样 prediff 在 单调区间有平坡的时候 就不会发生变化，造成我们的误判。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
// 局部最优->全局最优
// 删除单调坡上的中间节点(不包括两边节点)
if (nums.size() == 1) {
return 1;
}
// 使用down,up记录
int down = 1,up=1;
for(int j = 1;j<nums.size();j++) {
if(nums[j]>nums[j-1]) {
up = down+1;
}else if(nums[j]<nums[j-1]) {
down = up+1;
}
}
return max(down,up);
}
};
递增的三元序列
给你一个整数数组 nums ，判断这个数组中是否存在长度为 3 的递增子序列。
如果存在这样的三元组下标 (i, j, k) 且满足 i < j < k ，使得 nums[i] < nums[j] < nums[k] ，返回 true ；否则，返回 false 。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
bool increasingTriplet(vector<int>& nums) {
if (nums.size() < 3) {
return false;
}
int firstNum{nums[0]}, secondNum{numeric_limits<int>::max()};
for (int i = 1; i < nums.size(); ++i) {
int num = nums[i];
if (num > secondNum) {
return true;
} else if (num > firstNum) {
secondNum = num;
} else {
firstNum = num;
}
}
return false;
}
}
最大子数组和
给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。子数组是数组中的一个连续部分
局部最优：当前“连续和”为负数的时候立刻放弃，从下一个元素重新计算“连续和”，因为负数加上下一个元素 “连续和”只会越来越小。
全局最优：选取最大“连续和”.局部最优的情况下，并记录最大的“连续和”，可以推出全局最优。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int maxSubArray(vector<int>& nums) {
int result = INT32_MIN;
int count = 0;
for (int i = 0; i < nums.size(); i++) {
count += nums[i];
if (count > result) { // 取区间累计的最大值（相当于不断确定最大子序终止位置）
result = count;
}
if (count <= 0) count = 0; // 相当于重置最大子序起始位置，因为遇到负数一定是拉低总和
}
return result;
}
};
买卖股票最佳时期
给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
int maxProfit(vector<int>& prices) {
int maxProfit{};
// 记录遍历过程中的最小值
int lowPrice{numeric_limits<int>::max()};
int sz = prices.size();
for(int i = 0;i<sz;++i) {
lowPrice = min(lowPrice,prices[i]);
maxProfit = max(maxProfit,prices[i] - lowPrice);
}
return maxProfit;
}
};
买卖股票的最佳时机II
给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。
在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。
返回 你能获得的 最大 利润 。
需要收集每天的正利润就可以，收集正利润的区间，就是股票买卖的区间，而我们只需要关注最终利润，不需要记录区间。
那么只收集正利润就是贪心所贪的地方，局部最优：收集每天的正利润，全局最优：求得最大利润1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
int maxProfit(vector<int>& prices) {
int ans = 0;
int n = prices.size();
for (int i = 1; i < n; ++i) {
ans += max(0, prices[i] - prices[i - 1]);
}
return ans;
}
};
也可以动态规划1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int maxProfit(vector<int>& prices) {
// dp[i][1]第i天持有的最多现金
// dp[i][0]第i天持有股票后的最多现金
int n = prices.size();
vector<vector<int>> dp(n, vector<int>(2, 0));
dp[0][0] -= prices[0]; // 持股票
for (int i = 1; i < n; i++) {
// 第i天持股票所剩最多现金 = max(第i-1天持股票所剩现金, 第i-1天持现金-买第i天的股票)
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
// 第i天持有最多现金 = max(第i-1天持有的最多现金，第i-1天持有股票的最多现金+第i天卖出股票)
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
}
return max(dp[n - 1][0], dp[n - 1][1]);
}
};
K次取反后的最大值
给你一个整数数组 nums 和一个整数 k ，按以下方法修改该数组：
- 选择某个下标
i并将nums[i]替换为-nums[i]。
重复这个过程恰好 k 次。可以多次选择同一个下标 i 。
以这种方式修改数组后，返回数组 可能的最大和
贪心的思路，局部最优：让绝对值大的负数变为正数，当前数值达到最大，整体最优：整个数组和达到最大。局部最优可以推出全局最优。那么如果将负数都转变为正数了，K依然大于0，此时的问题是一个有序正整数序列，如何转变K次正负，让 数组和 达到最大。局部最优：只找数值最小的正整数进行反转，当前数值和可以达到最大（例如正整数数组{5, 3, 1}，反转1 得到-1 比 反转5得到的-5 大多了），全局最优：整个 数组和 达到最大1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
int largestSumAfterKNegations(vector<int>& nums, int k) {
// 按绝对值排序 如果是负数 k-1
sort(nums.begin(), nums.end(),
[](int a, int b) { return abs(a) > abs(b); });
int maxSum{};
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] < 0 && k > 0) {
k -= 1;
nums[i] = -nums[i];
}
}
if (k % 2 == 1) {
nums.back() = -nums.back();
}
for (auto n : nums) {
maxSum += n;
}
return maxSum;
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
int largestSumAfterKNegations(vector<int>& nums, int k) {
// 按绝对值排序 如果是负数 k-1
sort(nums.begin(), nums.end(),
[](int a, int b) { return abs(a) > abs(b); });
int maxSum{};
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] < 0 && k > 0) {
k -= 1;
nums[i] = -nums[i];
}
maxSum += nums[i];
}
if (k % 2 == 1) {
// nums.back() = -nums.back();
maxSum -= 2*abs(nums.back());
}
// for (auto n : nums) {
// maxSum += n;
// }
return maxSum;
}
};
加油站
在一条环路上有 N 个加油站，其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
int sz = gas.size();
int totalSum{},curSum{};
int start{};
for(int i = 0;i<sz;++i) {
totalSum += gas[i] - cost[i];
curSum += gas[i] - cost[i];
// 累加和如果小于0 不能选择该位置
if(curSum < 0) {
start = i+1;
curSum = 0;
}
}
if(totalSum<0) {
return -1;
}
return start;
}
};
分发糖果
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求，给这些孩子分发糖果：
- 每个孩子至少分配到
1个糖果。 - 相邻两个孩子中，评分更高的那个会获得更多的糖果。
请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
int candy(vector<int>& ratings) {
// 左右各一次遍历
int totalCandies{};
vector<int> candies(ratings.size(),1);
for(int i = 1;i<ratings.size();++i) {
if(ratings[i]>ratings[i-1]) {
candies[i] = candies[i-1]+1;
}
}
for(int i = ratings.size()-2;i>=0;--i) {
if(ratings[i]>ratings[i+1]) {
candies[i] = max(candies[i],candies[i+1]+1);
}
}
for(auto c:candies) {
totalCandies +=c;
}
return totalCandies;
}
};
根据身高重建队列
假设有打乱顺序的一群人站成一个队列，数组 people 表示队列中一些人的属性（不一定按顺序）。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ，前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ，其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性（queue[0] 是排在队列前面的人）。
本题有两个维度，h和k，看到这种题目一定要想如何确定一个维度，然后再按照另一个维度重新排列。
遇到两个维度权衡的时候，一定要先确定一个维度，再确定另一个维度。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
vector<vector<int>> result;
sort(people.begin(), people.end(), [](vector<int>& a, vector<int>& b) {
// 按照身高
if (a[0] != b[0]) {
return a[0] > b[0];
}
return a[1] < b[1];
});
for (int i = 0; i < people.size(); ++i) {
result.insert(result.begin() + people[i][1], people[i]);
}
return result;
}
};
或者在插入时使用list1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22// 版本二
class Solution {
public:
// 身高从大到小排（身高相同k小的站前面）
static bool cmp(const vector<int>& a, const vector<int>& b) {
if (a[0] == b[0]) return a[1] < b[1];
return a[0] > b[0];
}
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
sort (people.begin(), people.end(), cmp);
list<vector<int>> que; // list底层是链表实现，插入效率比vector高的多
for (int i = 0; i < people.size(); i++) {
int position = people[i][1]; // 插入到下标为position的位置
std::list<vector<int>>::iterator it = que.begin();
while (position--) { // 寻找在插入位置
it++;
}
que.insert(it, people[i]);
}
return vector<vector<int>>(que.begin(), que.end());
}
};
用最少数量的箭引爆气球
有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ，其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。
一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 x``start，x``end， 且满足 xstart ≤ x ≤ x``end，则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后，可以无限地前进。
给你一个数组 points ，返回引爆所有气球所必须射出的 最小 弓箭数 。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
int findMinArrowShots(vector<vector<int>>& points) {
sort(points.begin(), points.end(), [](vector<int>& a, vector<int>& b) {
if (a[0] != b[0]) {
return a[0] < b[0];
}
return a[1] < b[1];
});
int n = points.size();
if (n == 1) {
return 1;
}
int r{1};
for (int i = 1; i < n; ++i) {
if (points[i][0] > points[i-1][1]) { // 不相邻
r++;
}else{
points[i][1] = min(points[i-1][1],points[i][1]);
}
}
return r;
}
};
无重叠区间
给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。
注意 只在一点上接触的区间是 不重叠的。例如 [1, 2] 和 [2, 3] 是不重叠的1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
sort(intervals.begin(),intervals.end());
int r{};
for(int i = 0;i<intervals.size()-1;++i) {
if(intervals[i][1]<=intervals[i+1][0]) {
// 不重叠
continue;
}
// 重叠
// 选择更小结束值
r++;
intervals[i+1][1] = min(intervals[i+1][1],intervals[i][1]);
}
return r;
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 // 排序 按照结束时间 递增
class Solution {
public:
// 按照区间右边界排序
static bool cmp (const vector<int>& a, const vector<int>& b) {
return a[1] < b[1];
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if (intervals.size() == 0) return 0;
sort(intervals.begin(), intervals.end(), cmp);
int count = 1; // 记录非交叉区间的个数
int end = intervals[0][1]; // 记录区间分割点
for (int i = 1; i < intervals.size(); i++) {
if (end <= intervals[i][0]) { // 不交叉
end = intervals[i][1];
count++;
}
}
return intervals.size() - count;
}
};
划分字母区间
给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。例如，字符串 "ababcc" 能够被分为 ["abab", "cc"]，但类似 ["aba", "bcc"] 或 ["ab", "ab", "cc"] 的划分是非法的。
注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。
返回一个表示每个字符串片段的长度的列表。
在遍历的过程中相当于是要找每一个字母的边界，如果找到之前遍历过的所有字母的最远边界，说明这个边界就是分割点了。此时前面出现过所有字母，最远也就到这个边界了
可以分为如下两步：
- 统计每一个字符最后出现的位置
- 从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点
1 | class Solution { |
合并区间
以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
sort(intervals.begin(), intervals.end());
int n = intervals.size();
if (n == 1) {
return intervals;
}
vector<vector<int>> result;
result.push_back(intervals[0]);
for (int i = 1; i < n; ++i) {
if (intervals[i][0] > result.back()[1]) {
// 不重叠
result.push_back(intervals[i]);
} else {
// 重叠
result.back()[1] = max(intervals[i][1], result.back()[1]);
}
}
return result;
}
};
单调递增的数字
当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。
给定一个整数 n ，返回 小于或等于 n 的最大数字，且数字呈 单调递增 。
题目要求小于等于N的最大单调递增的整数，那么拿一个两位的数字来举例。
例如：98，一旦出现strNum[i - 1] > strNum[i]的情况（非单调递增），首先想让strNum[i - 1]—，然后strNum[i]给为9，这样这个整数就是89，即小于98的最大的单调递增整数。
这一点如果想清楚了，这道题就好办了。
此时是从前向后遍历还是从后向前遍历呢？
从前向后遍历的话，遇到strNum[i - 1] > strNum[i]的情况，让strNum[i - 1]减一，但此时如果strNum[i - 1]减一了，可能又小于strNum[i - 2]。
这么说有点抽象，举个例子，数字：332，从前向后遍历的话，那么就把变成了329，此时2又小于了第一位的3了，真正的结果应该是299。
那么从后向前遍历，就可以重复利用上次比较得出的结果了，从后向前遍历332的数值变化为：332 -> 329 -> 299
确定了遍历顺序之后，那么此时局部最优就可以推出全局，找不出反例，试试贪心1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
int monotoneIncreasingDigits(int n) {
string ns = to_string(n);
// 从后向前
int sz = ns.size();
int flag = sz;
// flag用来标记赋值9从哪里开始
// 设置为这个默认值，为了防止第二个for循环在flag没有被赋值的情况下执行
for(int i = sz-1;i>=1;i--) {
if(ns[i-1]>ns[i]) {
flag = i;
ns[i-1]--;
}
}
for(int t = flag;t<sz;t++) {
ns[t] = '9';
}
// 字符串转数字
return stoi(ns);
}
};
监控二叉树
给定一个二叉树，我们在树的节点上安装摄像头。节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。计算监控树的所有节点所需的最小摄像头数量。
把摄像头放在叶子节点的父节点位置，才能充分利用摄像头的覆盖面积。
为什么不从头结点开始看起呢，为啥要从叶子节点看呢？
因为头结点放不放摄像头也就省下一个摄像头， 叶子节点放不放摄像头省下了的摄像头数量是指数阶别的。所以要从下往上看，局部最优：让叶子节点的父节点安摄像头，所用摄像头最少，整体最优：全部摄像头数量所用最少！
局部最优推出全局最优，找不出反例，那么就按照贪心来. 使用后序
此时，大体思路就是从低到上，先给叶子节点父节点放个摄像头，然后隔两个节点放一个摄像头，直至到二叉树头结点。
此时这道题目还有两个难点：
- 二叉树的遍历
- 如何隔两个节点放一个摄像头
在二叉树中如何从低向上推导呢？
可以使用后序遍历也就是左右中的顺序，这样就可以在回溯的过程中从下到上进行推导了。
后序遍历代码如下：1
2
3
4
5
6
7
8
9
10
11int traversal(TreeNode* cur) {
// 空节点，该节点有覆盖
if (终止条件) return ;
int left = traversal(cur->left); // 左
int right = traversal(cur->right); // 右
逻辑处理 // 中
return ;
}
注意在以上代码中取了左孩子的返回值，右孩子的返回值，即left 和 right， 以后推导中间节点的状态
此时需要状态转移的公式，大家不要和动态的状态转移公式混到一起，本题状态转移没有择优的过程，就是单纯的状态转移！
来看看这个状态应该如何转移，先来看看每个节点可能有几种状态：
有如下三种：
- 该节点无覆盖
- 本节点有摄像头
- 本节点有覆盖
分别有三个数字来表示：
- 0：该节点无覆盖
- 1：本节点有摄像头
- 2：本节点有覆盖
1 | // 版本二 |
矩阵
螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
int left = 1,down = 0;
array<vector<int>,4> dirs{{{0,1},{1,0},{0,-1},{-1,0}}};
vector<int> result;
int totalNum = m*n;
int dirIndex{};
int start_x=0,start_y = 0;
vector<vector<bool>> visited(m,vector<bool>(n));
for(int i = 0;i<totalNum;++i) {
result.push_back(matrix[start_x][start_y]);
visited[start_x][start_y] = true;
int next_x = start_x + dirs[dirIndex][0];
int next_y = start_y + dirs[dirIndex][1];
if(next_x == m || next_x == -1 || next_y == n || next_y == -1 || visited[next_x][next_y]) {
dirIndex = (dirIndex+1)%4;
}
start_x = start_x+dirs[dirIndex][0];
start_y = start_y+dirs[dirIndex][1];
}
return result;
}
};
旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
// i行移动到n-1-i列
// j列移动到j行
// matrix_new[col][n−row−1]=matrix[row][col]
int n = matrix.size();
for(int i = 0;i<n/2;++i) {
// 针对每一行
for(int j = 0;j<(1+n)/2;j++) {
int temp = matrix[i][j];
// matrix_[i][j] = matrix[n-j-1][i]
matrix[i][j] = matrix[n-j-1][i];
matrix[n-j-1][i] = matrix[n-i-1][n-j-1];
matrix[n-i-1][n-j-1] = matrix[j][n-i-1];
matrix[j][n-i-1] = temp;
}
}
}
};
搜索二维矩阵
编写一个高效的算法来搜索 *m* x *n* 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
1 | class Solution { |
字串问题
和为k的子数组
1 | class Solution { |
滑动窗口最大值
给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
单调队列的经典题目.单调队列(通过deque,list实现)或者优先队列,总之要保证队列里单调递减或递增的原则，所以叫做单调队列1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34// priority_queue<pair<int,int>> pq;
// int sz = nums.size();
// vector<int> result;
// for(int i = 0;i<k;++i) {
// pq.push({nums.at(i),i}); // 第一个窗口 最大堆/优先队列 // 值与对应索引
// }
// result.push_back(pq.top().first);
// for(int i = k;i<sz;i++) {
// pq.emplace(nums.at(i),i);
// while(pq.top().second<=i-k) {
// pq.pop();
// }
// result.push_back(pq.top().first);
// }
// return result;
deque<int> dq;
vector<int> r;
int sz = nums.size();
// 双端队列中存索引,索引递增,存储的值是递减的
for(int i = 0;i<sz;i++) {
if(!dq.empty() && dq.front() == i-k) {
// 如果存在元素并且等于滑动窗口滑过去的索引 去除索引
dq.pop_front();
}
while(!dq.empty() && nums[dq.back()]<nums[i]) {
// 如果最小值小于当前值 剔除索引
dq.pop_back();
}
dq.push_back(i);
if(i>=k-1) {
r.push_back(nums.at(dq.front()));
}
}
return r;
我们需要一个队列，这个队列放进去窗口里的元素，然后随着窗口的移动，队列也一进一出，每次移动之后，队列告诉我们里面的最大值是什么.
队列里的元素一定是要排序的，而且要最大值放在出队口，要不然怎么知道最大值呢。
但如果把窗口里的元素都放进队列里，窗口移动的时候，队列需要弹出元素。
那么问题来了，已经排序之后的队列 怎么能把窗口要移除的元素（这个元素可不一定是最大值）弹出呢。队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队列里的元素数值是由大到小的。
C++中deque是stack和queue默认的底层实现容器，deque是可以两边扩展的，而且deque里元素并不是严格的连续分布的。
最小覆盖字串
1 | string minWindow(string s, string t) { |
栈与队列
栈提供push 和 pop 等等接口，所有元素必须符合先进后出规则，所以栈不提供走访功能，也不提供迭代器(iterator)。 不像是set 或者map 提供迭代器iterator来遍历所有元素。
- C++中stack，queue 是容器么？ 是容器适配器可以更换底层容器,deque,list
- 我们使用的stack，queue是属于那个版本的STL？SGI
- 我们使用的STL中stack，queue是如何实现的？ deque底层容器
- stack，queue 提供迭代器来遍历空间么？ 不提供
栈是以底层容器完成其所有的工作，对外提供统一的接口，底层容器是可插拔的（也就是说我们可以控制使用哪种容器来实现栈的功能）。
所以STL中栈往往不被归类为容器，而被归类为container adapter（容器适配器）。
以deque为缺省情况下栈的底层结构。deque是一个双向队列，只要封住一端，只开通另一端就可以实现栈的逻辑了。队列中先进先出的数据结构，同样不允许有遍历行为，不提供迭代器, 队列一样是以deque为缺省情况下的底部结构。
用栈实现队列
需要两个栈一个输入栈，一个输出栈，这里要注意输入栈和输出栈的关系。
在push数据的时候，只要数据放进输入栈就好，但在pop的时候，操作就复杂一些，输出栈如果为空，就把进栈数据全部导入进来（注意是全部导入），再从出栈弹出数据，如果输出栈不为空，则直接从出栈弹出数据就可以了。如果进栈和出栈都为空的话，说明模拟的队列为空了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41class MyQueue {
public:
stack<int> stIn;
stack<int> stOut;
/** Initialize your data structure here. */
MyQueue() {
}
/** Push element x to the back of queue. */
void push(int x) {
stIn.push(x);
}
/** Removes the element from in front of queue and returns that element. */
int pop() {
// 只有当stOut为空的时候，再从stIn里导入数据（导入stIn全部数据）
if (stOut.empty()) {
// 从stIn导入数据直到stIn为空
while(!stIn.empty()) {
stOut.push(stIn.top());
stIn.pop();
}
}
int result = stOut.top();
stOut.pop();
return result;
}
/** Get the front element. */
int peek() {
int res = this->pop(); // 直接使用已有的pop函数
stOut.push(res); // 因为pop函数弹出了元素res，所以再添加回去
return res;
}
/** Returns whether the queue is empty. */
bool empty() {
return stIn.empty() && stOut.empty();
}
};
用队列实现栈
队列模拟栈，其实一个队列就够了，队列是先进先出的规则，把一个队列中的数据导入另一个队列中，数据的顺序并没有变，并没有变成先进后出的顺序。
用两个队列que1和que2实现队列的功能，que2其实完全就是一个备份的作用，把que1最后面的元素以外的元素都备份到que2，然后弹出最后面的元素，再把其他元素从que2导回que1。
一个队列在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部，此时再去弹出元素就是栈的顺序了1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78class MyStack {
private:
queue<int>
qin; // 加入元素时,看是否为空,如果为空直接加入,否则将其中的元素加入到qout
// 再加入
queue<int> qout; // 弹出时弹出qin
public:
MyStack() {}
void push(int x) { qin.push(x); }
int pop() {
int size = qin.size();
size--;
while (size--) {
int n = qin.front();
qin.pop();
qout.push(n);
}
int r = qin.front();
qin.pop();
// 再把结果放回qin
qin = qout;
while(!qout.empty()) {
qout.pop();
}
return r;
}
int top() {
int size = qin.size();
size--;
while (size--) {
int n = qin.front();
qin.pop();
qout.push(n);
}
int r = qin.front();
qout.push(r);
qin.pop();
// 再把结果放回qin
qin = qout;
while(!qout.empty()) {
qout.pop();
}
return r;
// int t = pop();
// // 再把元素放回去
// while (!qin.empty()) {
// int n = qin.front();
// qout.push(n);
// qin.pop();
// }
// qin.push(t);
// while (!qout.empty()) {
// int n = qout.front();
// qin.push(n);
// qout.pop();
// }
// return t;
}
bool empty() {
if(qin.empty() && qout.empty()) {
return true;
}
return false;
}
};
/**
* Your MyStack object will be instantiated and called as such:
* MyStack* obj = new MyStack();
* obj->push(x);
* int param_2 = obj->pop();
* int param_3 = obj->top();
* bool param_4 = obj->empty();
*/
删除字符串中的所有相邻重复项
给出由小写字母组成的字符串 s，重复项删除操作会选择两个相邻且相同的字母，并删除它们。
在 s 上反复执行重复项删除操作，直到无法继续删除。在完成所有重复项删除操作后返回最终的字符串。答案保证唯一1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
string removeDuplicates(string s) {
string result;
for(auto ch:s) {
if(result.empty() || result.back()!=ch) {
result.push_back(ch);
}else{
result.pop_back();
}
}
return result;
}
};
可以拿字符串直接作为栈，这样省去了栈还要转为字符串的操作。
逆波兰表达式求值
给你一个字符串数组 tokens ，表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数
逆波兰表达式又叫后缀表达式,操作数在前,操作符在后
栈与递归之间在某种程度上是可以转换，逆波兰表达式相当于是二叉树中的后序遍历 ,可以把运算符作为中间节点，按照后序遍历的规则画出一个二叉树。逆波兰表达式是用后序遍历的方式把二叉树序列化1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
int evalRPN(vector<string>& tokens) {
// 力扣修改了后台测试数据，需要用longlong
stack<long long> st;
for (int i = 0; i < tokens.size(); i++) {
if (tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/") {
long long num1 = st.top();
st.pop();
long long num2 = st.top();
st.pop();
if (tokens[i] == "+") st.push(num2 + num1);
if (tokens[i] == "-") st.push(num2 - num1);
if (tokens[i] == "*") st.push(num2 * num1);
if (tokens[i] == "/") st.push(num2 / num1);
} else {
st.push(stoll(tokens[i]));
}
}
long long result = st.top();
st.pop(); // 把栈里最后一个元素弹出（其实不弹出也没事）
return result;
}
};
前k个高频元素
给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案. nums = [1,1,1,1,2,2,3,4], k = 2
优先队列->堆->完全二叉树
堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
// 桶排序或者优先队列
unordered_map<int,int> cnt;
for(auto num:nums) {
cnt[num]++;
}
// 使用优先队列, 因为要统计频率最高的k个数,
// priority_queue<pair<int,int>> pq; // 默认最大堆
auto comp = [](const pair<int,int>& a, const pair<int,int>& b) {
// 实现最小堆
// if(a.first==b.first) {
// return a.second>b.second;
// }
return a.first>b.first;
};
priority_queue<pair<int,int>,vector<pair<int,int>>,decltype(comp)> pq(comp); // 实现最小堆
for(auto p:cnt) {
pq.emplace(p.second,p.first);
if(pq.size()>k) {
pq.pop();
}
}
vector<int> r;
while(k--) {
r.push_back(pq.top().second);
pq.pop();
}
return r;
}
};
也可以使用桶排序
顾名思义，桶排序的意思是为每个值设立一个桶，桶内记录这个值出现的次数（或其它属性），然后对桶进行排序。针对样例来说，我们先通过桶排序得到四个桶 [1,2,3,4]，它们的值分别 为 [4,2,1,1]，表示每个数字出现的次数。
紧接着，我们对桶的频次进行排序，前 k 大个桶即是前 k 个频繁的数。这里我们可以使用各种排序算法，甚至可以再进行一次桶排序，把每个旧桶根据频次放在不同的新桶内。针对样例来说，因为目前最大的频次是 4，我们建立 [1,2,3,4] 四个新桶，它们分别放入的旧桶为 [[3,4],[2],[],[1]]，表示不同数字出现的频率。最后，我们从后往前遍历，直到找到 k 个旧桶。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
// 桶排序或者优先队列
unordered_map<int,int> cnt;
for(auto num:nums) {
cnt[num]++;
}
// 再使用一个map统计频次
unordered_map<int,vector<int>> cnt2;
for(auto p:cnt) {
cnt2[p.second].emplace_back(p.first);
}
vector<int> r;
for(int count = nums.size();count>=0;count--) {
if(cnt2.count(count)) {
for(auto v:cnt2[count]) {
r.emplace_back(v);
if(r.size()>=k) {
return r;
}
}
}
}
return r;
}
};
简化路径
给你一个字符串 path ，表示指向某一文件或目录的 Unix 风格 绝对路径 （以 '/' 开头），请你将其转化为 更加简洁的规范路径。
在 Unix 风格的文件系统中规则如下：
- 一个点
'.'表示当前目录本身。 - 此外，两个点
'..'表示将目录切换到上一级（指向父目录）。 - 任意多个连续的斜杠（即，
'//'或'///'）都被视为单个斜杠'/'。 - 任何其他格式的点（例如，
'...'或'....'）均被视为有效的文件/目录名称。
返回的 简化路径 必须遵循下述格式：
- 始终以斜杠
'/'开头。 - 两个目录名之间必须只有一个斜杠
'/'。 - 最后一个目录名（如果存在）不能 以
'/'结尾。 - 此外，路径仅包含从根目录到目标文件或目录的路径上的目录（即，不含
'.'或'..'）。
返回简化后得到的 规范路径 。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41class Solution {
public:
string simplifyPath(string path) {
vector<string> dirs;
for (int i = 0; i < path.size();) {
if (path[i] == '/') {
// 读到分隔符开始读路径
++i;
// 从不为/的路径开始
while (i < path.size() && path[i] == '/') {
i++;
}
if (i >= path.size()) {
// 结束
break;
}
// 读路径
string r;
while (i < path.size() && path[i] != '/') {
r += path[i];
i++;
}
if (r == "..") {
if (!dirs.empty()) {
dirs.pop_back();
}
} else if (r != ".") { // 如果为"."直接跳过 否则添加路径
dirs.push_back("/" + r);
}
}
}
if(dirs.empty()) {
return "/";
}
string result;
for (auto ch : dirs) {
result += ch;
}
return result;
}
};
滑动窗口
无重复字符最长字串
1 | class Solution { |
1 | class Solution { |
字符串的排列
给你两个字符串 s1 和 s2 ，写一个函数来判断 s2 是否包含 s1 的 排列。如果是，返回 true ；否则，返回 false 。换句话说，s1 的排列之一是 s2 的 子串 。
找到字符串中所有字母异位词
1 | class Solution { |
前缀和
二分法
二分查找（Binary Search），也叫折半查找，是一种在有序数组中查找特定元素的算法。它的核心思想是每次都通过比较中间元素，将搜索范围缩小一半，从而达到极高的查找效率。其时间复杂度为 O(logN)，这使得它在处理大规模有序数据时表现卓越。
二分查找的精髓在于其迭代地缩小搜索范围。无论具体问题如何，万变不离其宗的是以下几个要素：
- 明确搜索空间： 定义一个闭区间
[left, right]，表示当前可能包含目标解的范围。初始时，left通常是数组的起始索引，right是数组的结束索引。 - 计算中间点：
mid = left + (right - left) / 2。这种写法可以有效避免(left + right)可能导致的整数溢出，特别是在left和right都很大时。 - 比较与决策： 将
nums[mid]与目标值或某个条件进行比较。根据比较结果，有三种基本情况：- 找到了目标值（或满足条件）： 直接返回
mid或进行其他处理。 nums[mid]太小了： 说明目标值（或满足条件的解）在mid的右侧，更新left = mid + 1。nums[mid]太大了： 说明目标值（或满足条件的解）在mid的左侧，更新right = mid - 1或right = mid(取决于具体问题)。
- 找到了目标值（或满足条件）： 直接返回
- 循环终止条件： 循环通常持续到
left <= right或left < right。循环结束后，left和right的关系（例如left == right或left == right + 1）将指示最终的搜索结果。
在实际应用中，二分查找的循环终止条件和边界更新方式会根据“寻找什么”而略有不同。最常见的两种模式是：
- 查找特定值（或存在性）： 循环条件
while (left <= right)，当left > right时，表示整个搜索区间为空，未找到目标。- 如果
nums[mid] == target，返回mid。 - 如果
nums[mid] < target，left = mid + 1。 - 如果
nums[mid] > target，right = mid - 1。 - 特点：
left和right最终会越过彼此。
- 如果
- 查找边界（第一个/最后一个满足条件的元素）： 循环条件
while (left < right)，当left == right时，循环结束，left（或right）就是所求的索引。- 如果
nums[mid]满足条件：可能mid就是答案，也可能答案在mid的左侧。所以right = mid。 - 如果
nums[mid]不满足条件：答案肯定在mid的右侧。所以left = mid + 1。 - 特点：
left和right最终会收敛到同一个点。这种模式在寻找“第一个满足XX条件”或“最后一个满足XX条件”的问题中非常常见。
- 如果
循环不变量原则
循环不变量就像是你在循环执行过程中握住的“真理之绳”。无论循环执行了多少次，这条绳子所代表的性质都不会改变。
它通常由以下三个关键部分构成：
- 初始化（Initialization）：在进入循环之前，这个性质必须成立。
- 保持（Maintenance）：假设该性质在循环的某一次迭代开始时成立，那么在这次迭代结束时，它必须仍然成立。
- 终止（Termination）：当循环终止时，该性质与循环结束的条件结合起来，可以帮助我们证明算法的正确性。
写二分法经常写乱，主要是因为对区间的定义没有想清楚，区间的定义就是不变量。要在二分查找的过程中，保持不变量，就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作，这就是循环不变量规则。写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right).
当使用左闭右闭,区间的定义这就决定了二分法的代码应该如何写，因为定义target在[left, right]区间，所以有如下两点：
- while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
- if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1
如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) ，那么二分法的边界处理方式则截然不同。
有如下两点：
- while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
- if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]
1 | // 版本一 |
建议试一试用二分法
- 暴力解法时间复杂度：O(n)
- 二分法时间复杂度：O(logn)
只有在循环中坚持对区间的定义，才能清楚的把握循环中的各种细节。
在排序数组中查找第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值 target，返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
可以通过实现lower_bound和upper_bound查找第一个大于等于n和大于n的值对应索引1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41class Solution {
public:
int lower_bound(const vector<int>& nums,int n) {
// 找到第一个等于n的位置
int sz = nums.size();
int i = 0,j=sz;
while(i<j) {
int mid = (j-i)/2+i;
if(n>nums[mid]) {
i = mid+1;
}else{
j = mid;
}
}
return i;
}
int upper_bound(const vector<int>& nums,int n) {
int sz = nums.size();;
int i = 0,j = sz;
while(i<j) {
int mid = (j-i)/2+i;
if(n>=nums[mid]) {
i = mid+1;
}else{
j = mid;
}
}
return j;
}
vector<int> searchRange(vector<int>& nums, int target) {
// 排序查找 二分法
// lower_bound upper_bound
// 先找到等于的元素
int lower_indx = lower_bound(nums,target);
if(lower_indx == nums.size() || nums[lower_indx] !=target) {
return {-1,-1};
}
int uppper_indx = upper_bound(nums,target);
return {lower_indx,uppper_indx-1};
}
};
也可以直接进行查找第一个和最后一个值,通过更新索引1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47class Solution {
public:
int findFirstNum(vector<int>& nums, int target) {
int i = 0, j = nums.size();
int firstIndex = -1;
while (i < j) {
int mid = (j - i) / 2 + i;
if (nums[mid] == target) {
firstIndex = mid;
j = mid;
} else if (nums[mid] > target) {
j = mid ;
} else {
i = mid + 1;
}
}
return firstIndex;
}
int findLastIndex(vector<int>& nums, int target) {
int i = 0, j = nums.size();
int firstIndex = -1;
while (i < j) {
int mid = (j - i) / 2 + i;
if (nums[mid] == target) {
firstIndex = mid;
i = mid + 1;
} else if (nums[mid] > target) {
j = mid ;
} else {
i = mid + 1;
}
}
return firstIndex;
}
vector<int> searchRange(vector<int>& nums, int target) {
// 排序查找 二分法
// lower_bound upper_bound
// 先找到等于的元素
int lower_indx = findFirstNum(nums, target);
if (lower_indx == -1) {
return {-1, -1};
}
int last_index = findLastIndex(nums, target);
return {lower_indx,last_index};
}
};
寻找峰值
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
int findPeakElement(vector<int>& nums) {
int i = 0,j = nums.size();
while(i<j) {
int mid = (j-i)/2+i;
if((mid == 0 || nums[mid]>nums[mid-1]) && (mid == nums.size()-1 || nums[mid]>nums[mid+1])) {
// 满足峰值条件
return mid;
}else if(mid!=0 && nums[mid]<=nums[mid-1]) {
// 左边更大
// 左边一定存在峰值
j = mid;
}else {
// 右边更大
i = mid+1;
}
}
return i;
}
};
要实现 O(logn)时间复杂度，我们可以对数组进行二分查找。在确保两端不是峰值后，若当前中点不是峰值，那么其左右一侧一定有一个峰值。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24int findPeakElement(vector<int>& nums) {
int n = nums.size();
if (n == 1) {
return 0;
}
if (nums[0] > nums[1]) {
return 0;
}
if (nums[n - 1] > nums[n - 2]) {
return n - 1;
}
int l = 1, r = n - 2, mid;
while (l <= r) {
mid = l + (r - l) / 2;
if (nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]) {
return mid;
} else if (nums[mid] > nums[mid - 1]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
return -1;
}
搜索旋转排序数组
整数数组 nums 按升序排列，数组中的值 互不相同 。
在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 向左旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 下标 3 上向左旋转后可能变为 [4,5,6,7,0,1,2] 。给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
在普通的二分查找中，数组是完全有序的，我们可以通过比较中间元素和目标值来确定搜索方向。然而，在这个问题中，数组被旋转了，导致它不再完全有序。
但仔细观察，我们可以发现一个关键特性：无论数组如何旋转，它总会被中间的元素分成两个部分，其中至少一个部分是完全有序的。我们只需要在每次二分查找时，判断哪一部分是有序的，然后根据目标值是否在这个有序区间内来决定下一步的搜索方向。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32class Solution {
public:
int search(vector<int>& nums, int target) {
// 原本递增的数组,经过旋转之后
// 一段数字是递增,另一也是递增,前者大于等于后者
int i =0,j = nums.size()-1;
while(i<=j) {
int mid = (j-i)/2+i;
if(nums[mid] == target) {
return mid;
}
//1.首先需要判断[left,mid]是否有序
if(nums[i]<=nums[mid]) {
// 左半部分有序
if(target<nums[mid] && target>=nums[i]) {
j = mid-1; // 在左半部分
}else{
i = mid+1; //在右半部分
}
}else{
// 右半部分有序
if(target>nums[mid] && target<=nums[j]) {
// 在右半部分
i = mid+1;
}else{
j = mid-1; //在左半部分
}
}
}
return -1;
}
};
搜索旋转排序数组II
已知存在一个按非降序排列的整数数组 nums ，数组中的值不必互不相同。
在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转 ，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。
给你 旋转后 的数组 nums 和一个整数 target ，请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ，则返回 true ，否则返回 false 。你必须尽可能减少整个操作步骤。
对于数组中有重复元素的情况，二分查找时可能会有 a[l]=a[mid]=a[r]，此时无法判断区间 [l,mid] 和区间 [mid+1,r] 哪个是有序的。
例如 nums=[3,1,2,3,3,3,3]，target=2，首次二分时无法判断区间 [0,3] 和区间 [4,6] 哪个是有序的。
对于这种情况，我们只能将当前二分区间的左边界加一，右边界减一，然后在新区间上继续二分查找。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution {
public:
bool search(vector<int>& nums, int target) {
// 原本非降序的数组,经过旋转之后
// 一段数字是非降序,另一也是非降序,前者大于等于后者
int left = 0, right = nums.size() - 1;
while (left <= right) {
int mid = (right - left) / 2 + left;
if (nums[mid] == target) {
return true;
} else if ((nums[mid] == nums[left]) &&
(nums[mid] == nums[right])) {
// 两端都相等 无法确认有序区间
left++;
right--;
} else if (nums[mid] >= nums[left]) {
if (target >= nums[left] && target < nums[mid]) {
// 左半区间有序 并且target处在左半区间
right = mid - 1;
} else {
// 处在右半区间
left = mid + 1;
}
}else{
// 右半区间有序
if(target>nums[mid] && target<=nums[right]) {
left = mid+1;
}else{
right = mid-1;
}
}
}
return false;
}
};
单调栈
单调栈（Monotonic Stack）是一种特殊的栈数据结构，它在保持栈内元素严格单调递增或严格单调递减的同时，遍历处理输入序列。这种数据结构非常适合解决与“下一个更大/更小元素”相关的序列问题，因为它可以高效地找到每个元素左边或右边第一个比它大或小的元素，而无需进行嵌套循环。
单调栈的核心思想是“当一个元素入栈时，将所有不满足单调性的元素都弹出”。什么时候用单调栈呢？通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，此时我们就要想到可以用单调栈了。时间复杂度为O(n)。 例如每日温度就是求一个元素右边第一个比自己大的元素，此时就应该想到用单调栈了.单调栈的本质是空间换时间，因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素，优点是整个数组只需要遍历一次。
以单调递增栈（栈底到栈顶递增）为例：
- 遍历输入序列。
- 当前元素
x入栈：在x入栈之前，不断弹出栈顶元素y，直到栈为空或y < x。 - 为什么这样做？
- 对于每一个被弹出的元素
y，x就是它右边第一个比它小的元素。 - 通过这种方式，我们可以在一次遍历中，为每个元素找到它右边的第一个更小元素，时间复杂度仅为 O(n)。
- 对于每一个被弹出的元素
LeetCode 经典题目
单调栈在 LeetCode 上有许多经典应用，这些题目通常能让你深入理解其工作原理。
- 每日温度
问题描述：给定一个整数数组 temperatures，表示每天的温度。返回一个数组，其中 answer[i] 是指在第 i 天之后，至少需要等待多少天才能等到更暖和的温度。如果该天之后不存在更暖和的温度，则 answer[i] 为 0。
解题思路：
- 我们维护一个单调递减栈，栈中存储的是元素的索引。栈底到栈顶的索引对应的温度是递减的。
- 遍历温度数组：
- 如果当前温度
temperatures[i]大于栈顶索引j对应的温度temperatures[j]，说明我们找到了j右边第一个比它大的元素。 - 弹出栈顶索引
j，计算等待天数i - j，并将其存入结果数组answer[j]。 - 重复此过程，直到栈顶元素不比当前温度小。
- 最后，将当前索引
i压入栈中。
- 如果当前温度
- 栈中剩下的索引，意味着它们右边没有比它们更大的元素，对应的
answer值为 0。
1 | // LeetCode 739. 每日温度 |
- 柱状图中最大的矩形
问题描述：给定 n 个非负整数，表示一个柱状图，每个柱子的宽度为 1。找出这个柱状图中能形成的最大矩形面积。
解题思路：
- 要求最大矩形面积，可以转换为：对于每个柱子，找到以它为高的最大矩形。这个矩形的宽度由它左右两侧第一个比它低的柱子决定。
- 我们可以用两次单调栈遍历：
- 从左到右遍历，使用单调递增栈，找到每个柱子左边第一个比它低的柱子索引。
- 从右到左遍历，使用单调递增栈，找到每个柱子右边第一个比它低的柱子索引。
- 有了左右两边的索引，就可以计算以每个柱子为高的矩形面积，并找出最大值。
优化思路：
- 可以只用一次单调栈遍历来解决。
- 依然使用单调递增栈存储索引。当
heights[i]小于栈顶heights[top]时，heights[top]就是一个潜在的高度。 - 此时，
heights[top]的右边界是i，左边界是新的栈顶（如果栈不为空）或 -1。计算面积并更新最大值。
- 接雨水
问题描述：给定 n 个非负整数，表示一个柱状图，计算下雨后能接多少雨水。
解题思路：
- 可以用双指针或单调栈来解决。
- 使用单调递减栈存储索引。
- 遍历柱子数组：
- 当
heights[i]高于栈顶heights[top]时，说明heights[top]可能会形成一个凹槽。 - 弹出
top，它就是凹槽的底部。 - 新的栈顶
s.top()是凹槽的左壁，i是凹槽的右壁。 - 计算凹槽的高度
min(heights[i], heights[s.top()]) - heights[top]，宽度i - s.top() - 1，并累加雨水。
- 当
每日温度
请根据每日 气温 列表，重新生成一个列表。对应位置的输出为：要想观测到更高的气温，至少需要等待的天数。如果气温在这之后都不会升高，请在该位置用 0 来代替。
例如，给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
// 单调栈 可以找一个元素右侧/左侧的更大值/更小值
// 需要找更大值
// 单调减栈 从栈低到顶
stack<int> stk;
vector<int> result(temperatures.size(),0);
for(int i = 0;i<temperatures.size();i++) {
while(!stk.empty() && temperatures[stk.top()]<temperatures[i]) {
result[stk.top()] = i-stk.top();
stk.pop();
}
stk.push(i);
}
return result;
}
};
下一个更大元素I
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ，下标从 0 开始计数，其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ，找出满足 nums1[i] == nums2[j] 的下标 j ，并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素，那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案，满足 ans[i] 是如上所述的 下一个更大元素1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
int n1 = nums1.size();
int n2 = nums2.size();
unordered_map<int, int> umap;
for (int i = 0; i < n1; ++i) {
umap[nums1[i]] = i; // 记录索引
}
stack<int> s;
vector<int> r(n1, -1);
for (int i = 0; i < n2; ++i) {
while (!s.empty() && s.top() < nums2[i]) {
if (umap.count(s.top())) {
r[umap[s.top()]] = nums2[i];
}
s.pop();
}
s.push(nums2[i]);
}
return r;
}
};
下一个更大元素II
给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。
数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。
如何处理循环数组,可以想到由两个数组拼接,然后使用单调栈求下一个最大值就行
也可以不扩充nums，而是在遍历的过程中模拟走了两边nums1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
vector<int> nextGreaterElements(vector<int>& nums) {
int i{},sz = nums.size();
stack<int> stk;
vector<int> result(sz,-1);
for(int i = 0;i<2*sz;++i) {
while(!stk.empty() && nums[stk.top()]<nums[i%sz]) {
result[stk.top()] = nums[i%sz];
stk.pop();
}
stk.push(i%sz);
}
return result;
}
};
接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
相当于求左右侧第一个更大值的小值.每一列雨水的高度，取决于该列左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。 用到求右侧/左侧最大值/最小值就使用单调栈1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
int trap(vector<int>& height) {
// 使用单调栈 找到更大的柱
stack<int> stk;
int result{};
for (int i = 0; i < height.size(); ++i) {
while (!stk.empty() && height[i] > height[stk.top()]) {
// 遍历遇到的高度高于栈顶 此时栈顶元素是中间凹下去的柱子
int mid = stk.top();
stk.pop();
// 如果左侧没有值表示没有更高的高度了
if (!stk.empty()) {
int h = min(height[i], height[stk.top()]) - height[mid];
int w = i - stk.top()-1;
result += h*w;
}
}
stk.push(i);
}
return result;
}
};
柱状图中最大矩形
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。
本题是找每个柱子左右两边第一个小于该柱子的柱子。这里就涉及到了单调栈很重要的性质，就是单调栈里的顺序，是从小到大还是从大到小。
只有栈里从大到小的顺序，才能保证栈顶元素找到左右两边第一个小于栈顶元素的柱子。
所以本题单调栈的顺序正好与接雨水反过来。
此时大家应该可以发现其实就是栈顶和栈顶的下一个元素以及要入栈的三个元素组成了我们要求最大面积的高度和宽度
理解这一点，对单调栈就掌握的比较到位了。
除了栈内元素顺序和接雨水不同，剩下的逻辑就都差不多了，在题解42. 接雨水 (opens new window)我已经对单调栈的各个方面做了详细讲解，这里就不赘述了。
主要就是分析清楚如下三种情况：
- 情况一：当前遍历的元素heights[i]大于栈顶元素heights[st.top()]的情况
- 情况二：当前遍历的元素heights[i]等于栈顶元素heights[st.top()]的情况
- 情况三：当前遍历的元素heights[i]小于栈顶元素heights[st.top()]的情况
栈顶和栈顶的下一个元素以及要入栈的三个元素组成了我们要求最大面积的高度和宽度
在 height数组上后，都加了一个元素0， 为什么这么做呢？
首先来说末尾为什么要加元素0？
如果数组本身就是升序的，例如[2,4,6,8]，那么入栈之后 都是单调递减，一直都没有走 情况三 计算结果的哪一步，所以最后输出的就是0了.结尾加一个0，就会让栈里的所有元素，走到情况三的逻辑。
开头为什么要加元素0？如果数组本身是降序的，例如 [8,6,4,2]，在 8 入栈后，6 开始与8 进行比较，此时我们得到 mid（8），right（6），但是得不到 left。因为 将 8 弹出之后，栈里没有元素了，那么为了避免空栈取值，直接跳过了计算结果的逻辑。
之后又将6 加入栈（此时8已经弹出了），然后 就是 4 与 栈口元素 6 进行比较，周而复始，那么计算的最后结果result就是0。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
// 左右两侧最小值的最大值为高度
// 使用单调增栈 从栈底到顶 遇到小值
stack<int> stk;
int result{};
heights.push_back(0);
heights.insert(heights.begin(),0);
for (int i = 0; i < heights.size(); ++i) {
while (!stk.empty() && heights[i] < heights[stk.top()]) {
int mid = stk.top();
stk.pop();
if (!stk.empty()) {
// 计算高度
int h = heights[mid];
int w = i - stk.top() - 1;
result = max(result, h * w);
}
}
stk.push(i);
}
return result;
}
};
滑动窗口最大值
给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回 滑动窗口中的最大值 。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
// 单调队列
deque<int> dq; // 递减 队列首部存最大值
vector<int> result;
for (int i = 0; i < k; ++i) {
int n = nums[i];
while (!dq.empty() && n > dq.back()) {
dq.pop_back();
}
dq.push_back(n);
}
result.push_back(dq.front());
for (int i = k; i < nums.size(); i++) {
// 窗口向右移动
// 如果窗口移动超过了最大元素 弹出最大元素
if (nums[i - k] == dq.front()) {
dq.pop_front();
}
// 加入后面的元素
int n = nums[i];
while (!dq.empty() && n > dq.back()) {
dq.pop_back();
}
dq.push_back(n);
result.push_back(dq.front());
}
return result;
}
};
优先队列/堆
优先队列是一种抽象数据类型（ADT），它的核心特征是：
- 队列中的每个元素都有一个优先级。
- 队列总是按照优先级最高的元素进行出队（删除）操作。
- 元素的入队（插入）顺序不影响出队顺序，只与优先级有关。
你可以想象一个医院的急诊室：医生总是优先处理病情最严重的病人，而不是先到诊的病人。这就是一个优先队列的典型例子。
优先队列通常分为两种类型：
- 最大优先队列： 优先级最高的元素是最大的元素。
- 最小优先队列： 优先级最高的元素是最小的元素。
什么是堆？
堆是一种具体的数据结构，它通常是一个完全二叉树，并且满足特定的堆属性：
- 最大堆（Max Heap）： 任何一个父节点的值都大于或等于其子节点的值。因此，最大的元素总是在堆的根部。
- 最小堆（Min Heap）： 任何一个父节点的值都小于或等于其子节点的值。因此，最小的元素总是在堆的根部。
因为堆能够高效地找到最大或最小的元素，所以它成为了实现优先队列最常见、最有效的方式。在大多数编程语言中，当你使用“优先队列”时，底层往往就是一个堆。
堆可以通过完全二叉树实现堆排序.通过将数组构建成一个堆，然后不断地移除堆顶元素来完成排序。
堆排序主要分为两个步骤：
- 建堆（Heapify）： 将一个无序数组构建成一个堆。我们通常会构建一个最大堆（Max Heap），这样数组中最大的元素就会被放在数组的第一个位置（即堆顶）。
- 排序： 持续地从堆中移除最大的元素，并将其放到数组的正确位置上。
堆排序的关键在于一个名为 heapify 的操作。这个函数的作用是，确保以一个节点为根的子树满足堆的性质。以最大堆为例，heapify(arr, n, i) 函数会比较节点 i、它的左子节点和右子节点，找到这三个节点中最大的元素，并将其放在节点 i 的位置。如果发生了交换，就会对被交换的子树递归地调用 heapify，直到整个子树都满足最大堆的性质。
heapify 函数是堆排序的基础。它需要三个参数：数组 arr、堆的大小 n、以及要调整的子树的根节点索引 i。
heapSort 函数会调用 heapify 来完成建堆和排序两个步骤。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 堆调整函数：将以 i 为根节点的子树调整为最大堆
// n 是堆的当前大小
void heapify(std::vector<int>& arr, int n, int i) {
int largest = i; // 假设根节点是最大的
int left = 2 * i + 1; // 左子节点的索引
int right = 2 * i + 2; // 右子节点的索引
// 比较左子节点和根节点，更新 largest
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
// 比较右子节点和目前最大的节点，更新 largest
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// 如果最大的不是根节点，则进行交换
if (largest != i) {
std::swap(arr[i], arr[largest]);
// 递归地对被交换的子树进行堆调整
heapify(arr, n, largest);
}
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void heapSort(std::vector<int>& arr) {
int n = arr.size();
// 步骤1：建堆
// 从最后一个非叶子节点开始（索引为 n/2 - 1），
// 依次向上对每个子树进行堆调整，直到整个数组成为一个最大堆。
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
// 步骤2：排序
// 循环 n-1 次，每次从堆中移除一个最大元素并放到数组末尾
for (int i = n - 1; i > 0; i--) {
// 将当前堆顶（最大值）与堆的最后一个元素交换
// 此时，最大的元素已经位于数组的正确位置
std::swap(arr[0], arr[i]);
// 重新调整堆，忽略已经排序好的最后一个元素（i）
heapify(arr, i, 0);
}
}
数组中的第K个最大元素
给定整数数组 nums 和整数 k，请返回数组中第 **k** 个最大的元素。
请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62class Solution {
public:
int quickselect(vector<int>& nums, int l, int r, int k) {
if (l == r)
return nums[k];
int partition = nums[l], i = l - 1, j = r + 1;
while (i < j) {
do
i++;
while (nums[i] < partition);
do {
j--;
} while (nums[j] > partition);
if (i >= j) {
break;
}
swap(nums[i], nums[j]);
}
if (k <= j)
return quickselect(nums, l, j, k);
else
return quickselect(nums, j + 1, r, k);
}
void maxheapify(vector<int>& nums, int i, int sz) {
// 从叶子节点开始 构建堆
int leftNode = i*2+1;
int rightNode = i*2+2;
int largest = i;
if(leftNode<sz && nums[leftNode]>nums[largest]) {
largest = leftNode;
}
if(rightNode<sz && nums[rightNode]>nums[largest]) {
largest = rightNode;
}
if(largest!=i) {
swap(nums[largest],nums[i]); //交换两个子节点的最大值与当前值
maxheapify(nums,largest,sz); //largest对应位置为更小的值 需要再对该节点构建堆
}
}
int findKthLargest(vector<int>& nums, int k) {
// 建立最大堆,弹出k-1个元素后的元素
vector<int> heap = nums;
int sz = nums.size();
for (int i = sz - 1; i >= 0; --i) {
maxheapify(heap, (i - 1) / 2, sz);
}
k -=1;
while(k--) {
// 弹出值 交换到队尾
swap(heap[0],heap[sz-1]); // 将最大值弹出
sz--;
maxheapify(heap,0,sz);
}
return heap[0];
}
// int findKthLargest(vector<int> &nums, int k) {
// int n = nums.size();
// return quickselect(nums, 0, n - 1, n - k);
// }
};
合并k个有序链表
天际线
动态规划
动态规划（Dynamic Programming，简称 DP）是一种通过将复杂问题分解成更小的重叠子问题来求解的算法思想。它的核心在于避免重复计算，通过存储子问题的解来提高效率。
掌握动态规划的关键，在于理解它解决的两大核心问题：
- 最优子结构（Optimal Substructure）： 一个问题的最优解可以通过其子问题的最优解来构造。
- 重叠子问题（Overlapping Subproblems）： 在求解问题的过程中，需要多次计算同一个子问题。
动态规划的解题步骤
解决一个动态规划问题，通常可以遵循以下四个步骤，这就像一个解题模板：
- 确定 DP 状态（State）：
- 状态是动态规划的核心。你需要定义一个数组或表格
dp，其中dp[i]或dp[i][j]代表了解决某个子问题的解。 - 状态的定义必须能够唯一且完整地描述一个子问题。
- 例如： 在“爬楼梯”问题中，
dp[i]可以定义为“爬到第i级台阶的方法总数”。
- 状态是动态规划的核心。你需要定义一个数组或表格
- 确定状态转移方程（State Transition Equation）：
- 状态转移方程是连接子问题与原问题的桥梁。它描述了如何从一个或多个子问题的解，计算出当前问题的解。
- 例如： 在“爬楼梯”问题中，要爬到第
i级台阶，可以从第i-1级爬一步，或者从第i-2级爬两步。所以状态转移方程是dp[i] = dp[i-1] + dp[i-2]。
- 确定 DP 数组的初始值和边界条件：
- 动态规划的计算通常有一个起点。你需要为 DP 数组的最初几个元素（通常是
dp[0]或dp[0][0]）赋值。 - 这些初始值是递归的终止条件，它们必须是已知的、能够推导出后续所有状态的值。
- 例如： 在“爬楼梯”问题中，爬到第 0 级台阶只有 1 种方法（不动），
dp[0] = 1。爬到第 1 级台阶也只有 1 种方法（爬一步），dp[1] = 1。
- 动态规划的计算通常有一个起点。你需要为 DP 数组的最初几个元素（通常是
- 确定遍历顺序：
- 动态规划的计算是有依赖关系的。你需要按照一定的顺序（通常是从小到大或从左到右）遍历 DP 数组，确保在计算
dp[i]时，所有它依赖的子问题的解（如dp[i-1]、dp[i-2]）都已经计算完成。 - 例如： 在“爬楼梯”问题中，我们需要从
i = 2开始遍历，一直到n，因为dp[i]依赖于dp[i-1]和dp[i-2]。
- 动态规划的计算是有依赖关系的。你需要按照一定的顺序（通常是从小到大或从左到右）遍历 DP 数组，确保在计算
动态规划的解题套路
掌握了上述四个步骤后，我们可以通过一个简单的套路来解决大部分动态规划问题：
- 读题，识别动态规划问题： 如果问题可以分解为重叠子问题，并且需要求最优解（最大、最小、最多、最少），那么它很可能是动态规划。
- 定义 DP 数组： 勇敢地写下
dp[i]或dp[i][j]，并用一句话描述它的含义。 - 找递推关系（状态转移方程）： 思考如何从
dp[...小一些的索引...]得到dp[i]，这是最难的一步，通常需要举几个小例子来推导。 - 初始化 DP 数组： 确定
dp[0]、dp[0][0]等基本情况。 - 编写循环： 按照正确的依赖顺序，编写
for循环来填充 DP 数组。 - 返回结果： 根据 DP 数组的定义，返回最终需要的答案。
如果某一问题有很多重叠子问题，使用动态规划是最有效的。
所以动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的.对于动态规划问题，拆解为如下五步曲
- 确定dp数组（dp table）以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int climbStairs(int n) {
if (n <= 2) {
return n;
}
vector<int> dp(2);
// 初始化
dp[0] = 1;
dp[1] = 2;
int result{};
for (int i = 3; i <= n; i++) {
result = dp[0] + dp[1];
dp[0] = dp[1];
dp[1] = result;
}
return result;
}
};
爬楼梯II
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬至多m (1 <= m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢？
注意：给定 n 是一个正整数。输入描述：输入共一行，包含两个正整数，分别表示n, m
输出描述：输出一个整数，表示爬到楼顶的方法数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
using namespace std;
int main() {
int m,n;
// 最多爬m个台阶
cin>>n>>m;
// dp[i]表示到达i台阶的方法
vector<int> dp(n+1);
dp[0] = 1;
// 状态转移方程
// 完全背包
// dp[i] += dp[j] j = [i-n,i-1]
for(int i = 1;i<=n;++i) {
// 排列问题 先循环背包
for(int j = 1;j<=m;j++) {
// 完全背包 正序 可以重复取
if(i>=j) {
dp[i] += dp[i-j];
}
}
}
cout<<dp[n];
return 0;
}
使用最小花费爬楼梯
给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int n = cost.size();
if(n<2) {
return 0;
}
// 1. dp数组索引和对应数组含义 dp
// 2. 状态转移
// 3. 初始化
// 4. 遍历顺序
// 5. 举例推导数组
vector<int> dp(n+1);
dp[0] = 0;
dp[1] = 0;
for(int i =2;i<=n;++i) {
dp[i] = min(dp[i-1]+cost[i-1],cost[i-2]+dp[i-2]);
}
return dp[n];
}
};
不同路径
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。
问总共有多少条不同的路径？1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m,vector<int>(n));
// dp表示含义 到达m,n位置的路径数
for(int i = 0;i<m;++i) {
dp[i][0] = 1;
}
for(int i = 0;i<n;++i) {
dp[0][i] = 1;
}
// 初始化
// 遍历顺序
for(int i = 1;i<m;++i) {
for(int j =1;j<n;++j) {
dp[i][j] = dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
};
不同路径II
给定一个 m x n 的整数数组 grid。一个机器人初始位于 左上角（即 grid[0][0]）。机器人尝试移动到 右下角（即 grid[m - 1][n - 1]）。机器人每次只能向下或者向右移动一步。
网格中的障碍物和空位置分别用 1 和 0 来表示。机器人的移动路径中不能包含 任何 有障碍物的方格。返回机器人能够到达右下角的不同路径数量1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
vector<vector<int>> dp(m, vector<int>(n)); // dp表示
for (int i = 0; i < m && obstacleGrid[i][0] == 0; ++i) {
// 遇到障碍
dp[i][0] = 1;
}
for (int j = 0; j < n && obstacleGrid[0][j] == 0; ++j) {
dp[0][j] = 1;
}
if (obstacleGrid[0][0] == 1 || obstacleGrid[m - 1][n - 1] == 1) {
return 0;
}
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j) {
if (obstacleGrid[i][j] == 1) {
dp[i][j] = 0;
} else {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; // 状态转移方程
}
}
}
return dp[m - 1][n - 1];
}
};
整数拆分
给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
动态规划五部曲,分析如下:
- 确定dp数组以及下标含义,dp[i]表示数字可以拆分得到的最大乘积dp[i]
- 确定递推公式,
- 初始化
- 确定遍历顺序
- 模拟遍历
1 | class Solution { |
不同的二叉搜索树
给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数
确定dp数组（dp table）以及下标的含义
dp[i] ： 1到i为节点组成的二叉搜索树的个数为dp[i]。 dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
也可以理解是i个不同元素节点组成的二叉搜索树的个数为dp[i] ，都是一样的
dp[0]的初始化,从定义上来讲，空节点也是一棵二叉树，也是一棵二叉搜索树，这是可以说得通的。
从递归公式上来讲，dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量] 中以j为头结点左子树节点数量为0，也需要dp[以j为头结点左子树节点数量] = 1， 否则乘法的结果就都变成0了。
所以初始化dp[0] = 11
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int numTrees(int n) {
if(n<=2) {
return n;
}
vector<int> dp(n+1);
// 状态转换方程
// dp[i]表示i个节点组成的二叉搜索树的种树
dp[0] = 1; // 必须初始化 表示没有节点的nullptr二叉搜索树1种
dp[1] = 1;
dp[2] = 2;
for(int i = 3;i<=n;i++) {
for(int j = 1;j<=i;j++) {
// 以j为头节点
dp[i] += dp[j-1]*dp[i-j];
}
}
return dp[n];
}
};
01背包
有n件物品和一个最多能背重量为w的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。
- 确定dp数组以及下标的含义
需要使用二维数组，因为有两个维度需要分别表示：物品和背包容量.i 来表示物品、j表示背包容量。
- 状态转移方程
- 不放物品i：背包容量为j，里面不放物品i的最大价值是dp、[i - 1][j]。
- 放物品i：背包空出物品i的容量后，背包容量为j - weight[i]，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]且不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值
初始化
状态转移方程
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);可以看出i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包所能存放的最大价值。
那么很明显当
j < weight[0]的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小。当
j >= weight[0]时，dp[0][j] 应该是value[0]，因为背包容量放足够放编号0物品。确定遍历顺序
1 |
|
01背包一维滚动数组
1 | // 一维dp数组实现 |
分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等
确定dp数组以及下标含义
01背包中，dp[j] 表示： 容量（所能装的重量）为j的背包，所背的物品价值最大可以为dp[j]。如果背包所载重量为target， dp[target]就是装满 背包之后的总价值，因为 本题中每一个元素的数值既是重量，也是价值，所以，当 dp[target] == target 的时候，背包就装满了。
2.确定递推公式
01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题，相当于背包里放入数值，那么物品i的重量是nums[i]，其价值也是nums[i]。
所以递推公式：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])
3.dp数组如何初始化
从dp[j]的定义来看，首先dp[0]一定是0。
如果题目给的价值都是正整数那么非0下标都初始化为0就可以了，如果题目给的价值有负数，那么非0下标就要初始化为负无穷。
4.确定遍历顺序
如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历
1 | class Solution { |
最后一块石头的重量II
有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：
- 如果
x == y，那么两块石头都会被完全粉碎； - 如果
x != y，那么重量为x的石头将会完全粉碎，而重量为y的石头新重量为y-x。
最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
vector<int> dp(15001, 0);
int sum = 0;
for (int i = 0; i < stones.size(); i++) sum += stones[i];
int target = sum / 2;
for (int i = 0; i < stones.size(); i++) { // 遍历物品
for (int j = target; j >= stones[i]; j--) { // 遍历背包
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - dp[target] - dp[target];
}
};
目标和
给定一个非负整数数组，a1, a2, …, an, 和一个目标数，S。现在你有两个符号 + 和 -。对于数组中的任意一个整数，你都可以从 + 或 -中选择一个符号添加在前面。返回可以使最终数组和为目标数 S 的所有添加符号的方法数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum = 0;
for (int i = 0; i < nums.size(); i++) sum += nums[i];
if (abs(target) > sum) return 0; // 此时没有方案
if ((target + sum) % 2 == 1) return 0; // 此时没有方案
int bagSize = (target + sum) / 2;
vector<vector<int>> dp(nums.size(), vector<int>(bagSize + 1, 0));
// 初始化最上行
if (nums[0] <= bagSize) dp[0][nums[0]] = 1;
// 初始化最左列，最左列其他数值在递推公式中就完成了赋值
dp[0][0] = 1;
int numZero = 0;
for (int i = 0; i < nums.size(); i++) {
if (nums[i] == 0) numZero++;
dp[i][0] = (int) pow(2.0, numZero);
}
// 以下遍历顺序行列可以颠倒
for (int i = 1; i < nums.size(); i++) { // 行，遍历物品
for (int j = 0; j <= bagSize; j++) { // 列，遍历背包
if (nums[i] > j) dp[i][j] = dp[i - 1][j];
else dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];
}
}
return dp[nums.size() - 1][bagSize];
}
}
一维滚动数组,重复利用每一行的数值。
既然是重复利用每一行，就是将二维数组压缩成一行。
dp[i][j] 去掉 行的维度，即 dp[j]，表示：填满j（包括j）这么大容积的包，有dp[j]种方法。
二维DP数组递推公式： dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];
去掉维度i 之后，递推公式：dp[j] = dp[j] + dp[j - nums[i]] ，即：dp[j] += dp[j - nums[i]]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum = 0;
for (int i = 0; i < nums.size(); i++) sum += nums[i];
if (abs(target) > sum) return 0; // 此时没有方案
if ((target + sum) % 2 == 1) return 0; // 此时没有方案
int bagSize = (target + sum) / 2;
vector<int> dp(bagSize + 1, 0);
dp[0] = 1;
for (int i = 0; i < nums.size(); i++) {
for (int j = bagSize; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
return dp[bagSize];
}
};
一和零
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。
strs 数组里的元素就是物品，每个元素都是一个物品,而m 和 n相当于是一个背包，两个维度的背包
动规五部曲:
- dp数组。dp[i][j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]
1 | class Solution { |
完全背包
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
using namespace std;
int main() {
int n,v;
cin>>n>>v;
vector<int> weights(n);
vector<int> values(n);
for(int i = 0;i<n;++i) {
int wi,vi;
cin>>wi>>vi;
weights[i]=wi;
values[i]=vi;
}
// dp[i][j]数组含义 表示[0-i]的材料选择,容量为j下的最大价值
vector<vector<int>> dp(n,vector<int>(v+1));
// 初始化
for(int j = weights[0];j<=v;j++) {
dp[0][j] = dp[0][j-weights[0]]+values[0]; // 可重复取
}
// 遍历顺序
for(int i = 1;i<n;++i) {
for(int j = 0;j<=v;j++) {
if(j<weights[i]) {
// 容量小于当前i的重量 取上一个的值
dp[i][j] = dp[i-1][j];
}else{
dp[i][j] = max(dp[i-1][j],dp[i][j-weights[i]]+values[i]);
}
}
}
cout<<dp[n-1][v];
return 0;
}
零钱兑换II
给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。
假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带符号整数。
外层for循环遍历物品（钱币），内层for遍历背包（金钱总额），还是外层for遍历背包（金钱总额），内层for循环遍历物品（钱币）呢？
本题是求凑出来的方案个数，且每个方案个数是组合数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49class Solution {
public:
int change(int amount, vector<int>& coins) {
// 0 1数组
// 无限个 完全数组
int n = coins.size();
// dp索引和对应值
// dp[i][j] 表示[0-i]中选择,金额为j的组合数
// vector<long long> dp(amount + 1);
// 状态转移方程
// dp[i][j] += dp[z][j-coins[i]]
vector<vector<uint64_t>> dp(n,vector<uint64_t>(amount+1));
// 初始化
// 初始第一行
for(int j = 0;j<=amount;j++) {
if(j%coins[0] == 0) {
dp[0][j] = 1;
}
}
// 初始第一列
for(int i = 0;i<n;++i) {
dp[i][0] =1 ;
}
// 状态转移方程
for(int i = 1;i<n;++i) {
for(int j = 0;j<=amount;j++) {
if(j<coins[i]) {
dp[i][j] = dp[i-1][j];
}else{
// 可重复
dp[i][j] = dp[i-1][j]+dp[i][j-coins[i]];
}
}
}
return dp[n-1][amount];
//
// dp[0] = 1;
// for (int i = 0; i < n; ++i) {
// for (int j = coins[i]; j <= amount; j++) {
// if (dp[j] < INT_MAX - dp[j - coins[i]]) {
// dp[j] += dp[j - coins[i]];
// }
// }
// }
// return dp[amount];
}
};
组合总和IV
给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。题目数据保证答案符合 32 位整数范围。
说是求组合，但又说是可以元素相同顺序不同的组合算两个组合，其实就是求排列！
弄清什么是组合，什么是排列很重要。组合不强调顺序，(1,5)和(5,1)是同一个组合。排列强调顺序，(1,5)和(5,1)是两个不同的排列。如果求组合数就是外层for循环遍历物品，内层for遍历背包，
如果求排列数就是外层for遍历背包，内层for循环遍历物品**。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
int combinationSum4(vector<int>& nums, int target) {
int n = nums.size();
vector<uint64_t> dp(target + 1);
// dp[i]表示填充为i的组合个数
dp[0] = 1;
for (int i = 1; i <= target; i++) {
// 求排列 先遍历背包 再遍历物品
for (int j = 0; j < n; ++j) {
if (i >= nums[j]) {
dp[i] += dp[i - nums[j]];
}
}
}
return dp[target];
}
};
零钱兑换
给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。你可以认为每种硬币的数量是无限的1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
int n = coins.size();
// 可以重复取 完全背包
vector<int> dp(amount + 1, INT_MAX); // dp[i]表示金额凑到i的最少硬币数
dp[0] = 0;
for (int i = 0; i < n; ++i) {
for (int j = coins[i]; j <= amount; j++) {
if (dp[j - coins[i]] != INT_MAX) {
dp[j] = min(dp[j], dp[j - coins[i]] + 1);
}
}
}
return dp[amount] == INT_MAX?-1:dp[amount];
}
};
完全平方数
给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。
完全平方数就是物品（可以无限件使用），凑个正整数n就是背包，问凑满这个背包最少有多少物品？1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int numSquares(int n) {
// dp索引和值的含义
vector<int> dp(n + 1,INT_MAX);
// 表示和为i的完全平方数的最少数量dp[i]
dp[0] = 0;
// 初始化
// 状态转移方程 dp[i] += dp[i-j] + 1; j是完全平方数
// 完全背包 背包是num 物品是完全平方数
for (int i = 1; i <= n; ++i) {
for (int j = 1; j*j <= i; j++) {
// j是完全平方数
dp[i] = min(dp[i-j*j] + 1,dp[i]);
}
}
return dp[n];
}
};
动规五部曲分析如下：
- 确定dp数组（dp table）以及下标的含义
dp[j]：和为j的完全平方数的最少数量为dp[j]
2.确定递推公式
dp[j] 可以由dp[j - i i]推出， dp[j - i i] + 1 便可以凑成dp[j]。
此时我们要选择最小的dp[j]，所以递推公式：dp[j] = min(dp[j - i * i] + 1, dp[j]);
3.dp数组如何初始化
dp[0]表示 和为0的完全平方数的最小数量，那么dp[0]一定是0。
从递归公式dp[j] = min(dp[j - i i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的，*所以非0下标的dp[j]一定要初始为最大值，这样dp[j]在递推的时候才不会被初始值覆盖。
- 确定遍历顺序
这是完全背包，如果求组合数就是外层for循环遍历物品，内层for遍历背包。如果求排列数就是外层for遍历背包，内层for循环遍历物品。本题也是一样的，是求最小数,本题外层for遍历背包，内层for遍历物品，还是外层for遍历物品，内层for遍历背包，都是可以的
单词拆分
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。
- 确定dp数组以及下标的含义
dp[i] : 字符串长度为i的话，dp[i]为true，表示可以拆分为一个或多个在字典中出现的单词
- 确定递推公式
如果确定dp[j] 是true，且 [j, i] 这个区间的子串出现在字典里，那么dp[i]一定是true
3.dp数组如何初始化
从递推公式中可以看出，dp[i] 的状态依靠 dp[j]是否为true，那么dp[0]就是递推的根基，dp[0]一定要为true，否则递推下去后面都都是false了
4.确定遍历顺序
题目中说是拆分为一个或多个在字典中出现的单词，所以这是完全背包。
还要讨论两层for循环的前后顺序。
如果求组合数就是外层for循环遍历物品，内层for遍历背包如果求排列数就是外层for遍历背包，内层for循环遍历物品1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
// 完全背包
// 物品可以重复原则 物品是wordDict中字段
// 排列 先循环背包
unordered_set<string> uset(wordDict.begin(), wordDict.end());
int n = wordDict.size();
// dp含义 利用字典的单词到i个字符能否拼接
// 状态转移方程
// if(dp[j] && [j-i]的字符串在uset中包含)
vector<int> dp(s.size() + 1);
dp[0] = true;
for (int i = 1; i <= s.size(); i++) {
// 再遍历物品
for (int j = 0; j <= i; j++) {
string str = s.substr(j, i - j);
if (dp[j] && uset.count(str)) {
dp[i] = true;
}
}
}
return dp[s.size()];
}
};
打家劫舍
你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
int rob(vector<int>& nums) {
// dp数组含义
// dp[i] 表示考虑i / 到达i偷窃到的最高金额 int n = nums.size();
int n =nums.size();
if (n == 1) {
return nums[0];
}
if (n == 2) {
return max(nums[0], nums[1]);
}
vector<int> dp(n);
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
// 状态转移
// dp[i] = max(dp[i-1],dp[i-2]+nums[i]) // 偷当前值和不偷的最大值
for (int i = 2; i < n; ++i) {
dp[i] =
max(dp[i - 1], dp[i - 2] + nums[i]); // 偷当前值和不偷的最大值
}
return dp[n-1];
}
};
打家劫舍II
你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36class Solution {
public:
int rob_(vector<int>&nums, int l,int r) {
int n = r-l;
if(n == 1){
return nums[l];
}
if(n == 2) {
return max(nums[l],nums[l+1]);
}
vector<int> dp(n);
dp[0] = nums[l];
dp[1] = max(nums[l],nums[l+1]);
for(int i = 2;i<n;i++) {
dp[i] = max(dp[i-2]+nums[l+i],dp[i-1]);
}
return dp[n-1];
}
int rob(vector<int>& nums) {
// 不能首尾都偷
// 所以有两种方式
int n = nums.size();
if(n == 1) {
return nums[0];
}
if(n == 2){
return max(nums[0],nums[1]);
}
// 考虑0-n-2
int left =rob_(nums,0,n-1);
// 考虑 1-n-1
int right =rob_(nums,1,n);
return max(left,right);
}
};
对于一个数组，成环的话主要有如下三种情况：
情况一：考虑不包含首尾元素
情况二：考虑包含首元素，不包含尾元素
情况三：考虑包含尾元素，不包含首元素
注意这里用的是”考虑”，虽然考虑包含尾元素，但不一定要选尾部元素,而情况二 和 情况三 都包含了情况一了，所以只考虑情况二和情况三就可以了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int rob(vector<int>& nums) {
if (nums.size() == 0) return 0;
if (nums.size() == 1) return nums[0];
int result1 = robRange(nums, 0, nums.size() - 2); // 情况二
int result2 = robRange(nums, 1, nums.size() - 1); // 情况三
return max(result1, result2);
}
// 198.打家劫舍的逻辑
int robRange(vector<int>& nums, int start, int end) {
if (end == start) return nums[start];
vector<int> dp(nums.size());
dp[start] = nums[start];
dp[start + 1] = max(nums[start], nums[start + 1]);
for (int i = start + 2; i <= end; i++) {
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[end];
}
};
打家劫舍III
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。
除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。给定二叉树的 root 。返回 *在不触动警报的情况下 ，小偷能够盗取的最高金额* 。
记忆化搜索1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
unordered_map<TreeNode* , int> umap; // 记录计算过的结果
int rob(TreeNode* root) {
if (root == NULL) return 0;
if (root->left == NULL && root->right == NULL) return root->val;
if (umap[root]) return umap[root]; // 如果umap里已经有记录则直接返回
// 偷父节点
int val1 = root->val;
if (root->left) val1 += rob(root->left->left) + rob(root->left->right); // 跳过root->left
if (root->right) val1 += rob(root->right->left) + rob(root->right->right); // 跳过root->right
// 不偷父节点
int val2 = rob(root->left) + rob(root->right); // 考虑root的左右孩子
umap[root] = max(val1, val2); // umap记录一下结果
return max(val1, val2);
}
};
动态规划其实就是使用状态转移容器来记录状态的变化，这里可以使用一个长度为2的数组，记录当前节点偷与不偷所得到的的最大金钱。
树形dp的入门题目，因为是在树上进行状态转移，我们在讲解二叉树的时候说过递归三部曲，下面以递归三部曲为框架，其中融合动规五部曲的内容来
- 确定递归函数的参数和返回值
这们要求一个节点 偷与不偷的两个状态所得到的金钱，那么返回值就是一个长度为2的数组。
参数为当前节点,其实这里的返回数组就是dp数组。
所以dp数组（dp table）以及下标的含义：下标为0记录不偷该节点所得到的的最大金钱，下标为1记录偷该节点所得到的的最大金钱。
2.确定终止条件
在遍历的过程中，如果遇到空节点的话，很明显，无论偷还是不偷都是0，所以就返回
3.确定遍历顺序
首先明确的是使用后序遍历。 因为要通过递归函数的返回值来做下一步计算。
通过递归左节点，得到左节点偷与不偷的金钱。
通过递归右节点，得到右节点偷与不偷的金钱。
4.单层递归逻辑
如果是偷当前节点，那么左右孩子就不能偷，val1 = cur->val + left[0] + right[0];
如果不偷当前节点，那么左右孩子就可以偷，至于到底偷不偷一定是选一个最大的，所以：val2 = max(left[0], left[1]) + max(right[0], right[1]);1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution {
public:
// unordered_map<TreeNode*, int> umap;
vector<int> robTree(TreeNode* node) {
// 递归函数返回值 偷或者不偷这个节点的最大金额
// 递归结束条件
if(node == nullptr){
return {0,0};
}
// 递归函数执行
vector<int> l = robTree(node->left);
vector<int> r = robTree(node->right);
// 后序遍历
// 动态规划转移方程
// 偷这个节点 值为这个节点值加上不偷子节点的值
int f1 = node->val + l[1] + r[1];
// 不偷 值为偷或者不偷子节点的最大值
int f2 = max(l[0],l[1]) + max(r[0],r[1]);
return {f1,f2};
}
int rob(TreeNode* root) {
if (!root) {
return 0;
}
vector<int> r = robTree(root);
return max(r[0],r[1]);
}
};
买卖股票最佳时机
给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。
贪心1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
int maxProfit(vector<int>& prices) {
// 记录最小值 更新最大值
int minPrice = INT_MAX;
int maxProfit = INT_MIN;
for(int i = 0;i<prices.size();++i) {
minPrice = min(minPrice,prices[i]);
maxProfit = max(prices[i]-minPrice,maxProfit);
}
return maxProfit;
}
};
动态规划.
动规五部曲分析如下：
- 确定dp数组（dp table）以及下标的含义
dp[i][0] 表示第i天持有股票所得最多现金,一开始现金是0，那么加入第i天买入股票现金就是 -prices[i]， 这是一个负数。dp[i][1] 表示第i天不持有股票所得最多现金
2.确定递推公式
如果第i天持有股票即dp[i][0]， 那么可以由两个状态推出来
- 第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金 即：dp[i - 1][0]
- 第i天买入股票，所得现金就是买入今天的股票后所得现金即：-prices[i] 因为只能进行一次买卖,当买入后持有的现金就是-prices[i]
那么dp[i][0]应该选所得现金最大的，所以dp[i][0] = max(dp[i - 1][0], -prices[i]);
如果第i天不持有股票即dp[i][1]， 也可以由两个状态推出来
- 第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金 即：dp[i - 1][1]
- 第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金即：prices[i] + dp[i - 1][0]
同样dp[i][1]取最大的，dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
3.dp数组如何初始化
由递推公式 dp[i][0] = max(dp[i - 1][0], -prices[i]); 和 dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);可以看出其基础都是要从dp[0][1]推导。
那么dp[0][0]表示第0天持有股票，此时的持有股票就一定是买入股票了，因为不可能有前一天推出来，所以dp[0][0] -= prices[0];dp[0][1]表示第0天不持有股票，不持有股票那么现金就是0，所以dp[0][1] = 0;
4.确定遍历顺序
从递推公式可以看出dp[i]都是由dp[i - 1]推导出来的，那么一定是从前向后遍历。
5.举例推导dp数组1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int maxProfit(vector<int>& prices) {
// 动态规划
// 记录某一天买或者卖股票的最大利润
int n = prices.size();
vector<vector<int>> dp(n, vector<int>(2));
// dp[n][0]当前没有持有股票的最大利润
// dp[n][1]表示持有股票的最大利润
// dp[i][0] = max(dp[i-1][0],dp[i][1]+prices[i])
// dp[i][1] = max(dp[i-1][1],dp[i][0]-prices[i])
dp[0][0] = 0;
dp[0][1] = -prices[0];
for (int i = 1; i < n; ++i) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = max(dp[i - 1][1], -prices[i]);
}
return dp[n - 1][0];
}
}
买卖股票最佳时机II
给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。
在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。返回 你能获得的 最大 利润 。
贪心,加上每一个增加的区间值1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
int maxProfit(vector<int>& prices) {
// 只能最多持有一股
// 可以同1天出售
int maxP{};
// 计算递增区间值
for(int i = 1;i<prices.size();++i) {
maxP += max(prices[i]-prices[i-1],0);
}
return maxP;
}
};
动态规划,可以买卖多次,也就是持有股票时的利润与上一次没有持有股票的最大利润有关,如果只能买卖一次,持有股票的利润就是max(上一次持有股票最大利润,股票价格).1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
int maxProfit(vector<int>& prices) {
// 动态规划
int n = prices.size();
vector<vector<int>> dp(n,vector<int>(2));
dp[0][1] = -prices[0]; //持有股票的最大利润
for(int i = 1;i<n;++i) {
dp[i][0] = max(dp[i-1][0],dp[i-1][1]+prices[i]);
dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i]);
}
return *max_element(dp[n-1].begin(),dp[n-1].end());
}
};
买卖股票的最佳时机III
给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）
关键在于至多买卖两次，这意味着可以买卖一次，可以买卖两次，也可以不买卖。
用动态规划五部曲详细分析一下：
- 确定dp数组以及下标的含义
一天一共就有五个状态，
- 没有操作 （其实我们也可以不设置这个状态）
- 第一次持有股票
- 第一次不持有股票
- 第二次持有股票
- 第二次不持有股票
2.确定递推公式
达到dp[i][1]状态，有两个具体操作：
- 操作一：第i天买入股票了，那么dp[i][1] = dp[i-1][0] - prices[i]
- 操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][1] = dp[i - 1][1]
选最大的，所以 dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][1]);
同理dp[i][2]也有两个操作：
- 操作一：第i天卖出股票了，那么dp[i][2] = dp[i - 1][1] + prices[i]
- 操作二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i][2] = dp[i - 1][2]
所以dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])
同理可推出剩下状态部分：
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
3.dp数组如何初始化
第0天没有操作，这个最容易想到，就是0，即：dp[0][0] = 0;
第0天做第一次买入的操作，dp[0][1] = -prices[0];
第0天做第一次卖出的操作，这个初始值应该是多少呢？
此时还没有买入，怎么就卖出呢？ 其实大家可以理解当天买入，当天卖出，所以dp[0][2] = 0;
第二次买入依赖于第一次卖出的状态，其实相当于第0天第一次买入了，第一次卖出了，然后再买入一次（第二次买入），那么现在手头上没有现金，只要买入，现金就做相应的减少。
所以第二次买入操作，初始化为：dp[0][3] = -prices[0];
同理第二次卖出初始化dp[0][4] = 0;
4.确定遍历顺序
从递归公式其实已经可以看出，一定是从前向后遍历，因为dp[i]，依靠dp[i - 1]的数值。
5.举例推导dp数组1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class Solution {
public:
int maxProfit(vector<int>& prices) {
// 最多完成两笔交易
// 定义多种状态
// dp[i][4]
int n = prices.size();
vector<vector<int>> dp(n, vector<int>(5));
// 不做操作
// 第一次持有股票
// 第一次不持有股票 卖出第一次持有股票状态
// 第二次持有股票
// 第二次不持有股票
// 递归公式
// dp[i][1] = max(dp[i-1][1],dp[i-1][2]-prices[i]);
// dp[i][2] = max(dp[i-1][2],dp[i-1][1]+prices[i]);
// dp[i][3] = max(max(dp[i-1][3],dp[i-1][1]-prices[i]);
// dp[i][4] = max(max(dp[i-1][4],dp[i-1][3]+prices[i]);
// 初始化数组
dp[0][1] = -prices[0];
dp[0][3] = -prices[0];
for (int i = 1; i < n; ++i) {
dp[i][0] = dp[i-1][0];
dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i]);
dp[i][2] = max(dp[i-1][2],dp[i-1][1]+prices[i]);
dp[i][3] = max(dp[i-1][3],dp[i-1][2]-prices[i]);
dp[i][4] = max(dp[i-1][4],dp[i-1][3]+prices[i]);
}
return dp[n - 1][4];
}
};
最大的时候一定是卖出的状态，而两次卖出的状态现金最大一定是最后一次卖出。如果第一次卖出已经是最大值了，那么可以在当天立刻买入再立刻卖出。所以dp[4][4]已经包含了dp[4][2]的情况。也就是说第二次卖出手里所剩的钱一定是最多的。
买卖股票的最佳时机IV
给你一个整数数组 prices 和一个整数 k ，其中 prices[i] 是某支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说，你最多可以买 k 次，卖 k 次。注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
if (prices.size() == 0) return 0;
vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
for (int j = 1; j < 2 * k; j += 2) {
dp[0][j] = -prices[0];
}
for (int i = 1;i < prices.size(); i++) {
for (int j = 0; j < 2 * k - 1; j += 2) {
dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}
}
return dp[prices.size() - 1][2 * k];
}
};
动规五部曲，分析如下：
- 确定dp数组以及下标的含义
使用二维数组 dp[i][j] ：第i天的状态为j，所剩下的最大现金是dp[i][j]
j的状态表示为：
0 表示不操作
1 第一次买入
2 第一次卖出
3 第二次买入
4 第二次卖出
…..
除了0以外，偶数就是卖出，奇数就是买入
2.确定递推公式
还要强调一下：dp[i][1]，表示的是第i天，买入股票的状态，并不是说一定要第i天买入股票，这是很多同学容易陷入的误区。
达到dp[i][1]状态，有两个具体操作：
- 操作一：第i天买入股票了，那么dp[i][1] = dp[i - 1][0] - prices[i]
- 操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][1] = dp[i - 1][1]
选最大的，所以 dp[i][1] = max(dp[i - 1][0] - prices[i], dp[i - 1][1]);
同理dp[i][2]也有两个操作：
- 操作一：第i天卖出股票了，那么dp[i][2] = dp[i - 1][1] + prices[i]
- 操作二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i][2] = dp[i - 1][2]
所以dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])
3.dp数组如何初始化
第0天没有操作，这个最容易想到，就是0，即：dp[0][0] = 0;
第0天做第一次买入的操作，dp[0][1] = -prices[0];
第0天做第一次卖出的操作，这个初始值应该是多少呢？
此时还没有买入，怎么就卖出呢？ 其实大家可以理解当天买入，当天卖出，所以dp[0][2] = 0;
第0天第二次买入操作，初始值应该是多少呢？应该不少同学疑惑，第一次还没买入呢，怎么初始化第二次买入呢？
第二次买入依赖于第一次卖出的状态，其实相当于第0天第一次买入了，第一次卖出了，然后在买入一次（第二次买入），那么现在手头上没有现金，只要买入，现金就做相应的减少。
所以第二次买入操作，初始化为：dp[0][3] = -prices[0];
第二次卖出初始化dp[0][4] = 0;所以同理可以推出dp[0][j]当j为奇数的时候都初始化为 -prices[0]
4.遍历顺序 从递归公式其实已经可以看出，一定是从前向后遍历，因为dp[i]，依靠dp[i - 1]的数值。
5.举例推导
题目要求是至多有K笔交易，那么j的范围就定义为 2 * k + 1 就可以了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
// 进行k笔交易
// III的进阶版
// 定义dp数组
int n = prices.size();
// dp[i][j]表示含义 第i天
// 0 不做操作
// 第1次买入 第一次持有
// 第一次卖出 第一次不持有
// ...
vector<vector<int>> dp(n, vector<int>(2 * k + 1));
// 状态转移方程
// j == 0 dp[i][j] = dp[i-1][j]
// if(j%2 == 1) // 买入
// dp[i][j] = max(dp[i-1][j],dp[i-1][j-1]-prices[i]);
// if(j!=0 && j%2 == 0) //
// dp[i][j] = max(dp[i-1][j],dp[i-1][j-1]+prices[i]);
// 初始化数组
// 买入 j%2==1
for (int j = 1; j < 2 * k + 1; j += 2) {
dp[0][j] = -prices[0]; // 初始化每次买入的最大利润 也就是第一天股票价格
}
for (int i = 1; i <n; i++) {
dp[i][0] = dp[i - 1][0];
for (int j = 1; j < 2 * k + 1; j++) {
if (j % 2 == 1) {
// 买入
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1] - prices[i]);
}else{
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1] + prices[i]);
}
}
}
return dp[n-1][2*k];
}
};
买卖股票最佳时期含冷冻期
给定一个整数数组prices，其中第 prices[i] 表示第 *i* 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:
- 卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）
要单独列出”今天卖出状态”,冷冻期的前一天，只能是 「今天卖出股票」状态，如果是 「不持有股票状态」那么就很模糊，因为不一定是 卖出股票的操作。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int maxProfit(vector<int>& prices) {
// 有哪些状态
// 买入状态 持有股票状态
// 卖出状态 前一天是冷冻期或者是卖出状态 不是当天卖出
// 今天卖出状态 卖出后进入冷冻状态
// 冷冻状态 只保持一天
int n = prices.size();
vector<vector<int>> dp(n,vector<int>(4));
dp[0][0] = -prices[0];
// 状态转移
for(int i = 1;i<n;++i) {
dp[i][0] = max(max(dp[i-1][0],dp[i-1][3]-prices[i]),dp[i-1][1]-prices[i]);
dp[i][1] = max(dp[i-1][1],dp[i-1][3]);
dp[i][2] = dp[i-1][0]+prices[i]; // 今天卖出状态 只能由前一天的买入状态到达
dp[i][3] = dp[i-1][2]; // 冷冻状态也只能由前一天的卖出状态到达
}
return max(max(dp[n-1][1],dp[n-1][3]),dp[n-1][2]);
}
};
动规五部曲，分析如下：
- 确定dp数组以及下标的含义
dp[i][j]，第i天状态为j，所剩的最多现金为dp[i][j]。
具体可以区分出如下四个状态：
- 状态一：持有股票状态（今天买入股票，或者是之前就买入了股票然后没有操作，一直持有）
- 不持有股票状态，这里就有两种卖出股票状态
- 状态二：保持卖出股票的状态（两天前就卖出了股票，度过一天冷冻期。或者是前一天就是卖出股票状态，一直没操作）
- 状态三：今天卖出股票
- 状态四：今天为冷冻期状态，但冷冻期状态不可持续，只有一天
2.确定递推公式
达到买入股票状态（状态一）即：dp[i][0]，有两个具体操作：
- 操作一：前一天就是持有股票状态（状态一），dp[i][0] = dp[i - 1][0]
- 操作二：今天买入了，有两种情况
- 前一天是冷冻期（状态四），dp[i - 1][3] - prices[i]
- 前一天是保持卖出股票的状态（状态二），dp[i - 1][1] - prices[i]
那么dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]);
达到保持卖出股票状态（状态二）即：dp[i][1]，有两个具体操作：
- 操作一：前一天就是状态二
- 操作二：前一天是冷冻期（状态四）
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
达到今天就卖出股票状态（状态三），即：dp[i][2] ，只有一个操作：
昨天一定是持有股票状态（状态一），今天卖出
即：dp[i][2] = dp[i - 1][0] + prices[i];
达到冷冻期状态（状态四），即：dp[i][3]，只有一个操作：
昨天卖出了股票（状态三）
dp[i][3] = dp[i - 1][2];
3.dp数组如何初始化
这里主要讨论一下第0天如何初始化。
如果是持有股票状态（状态一）那么：dp[0][0] = -prices[0]，一定是当天买入股票。
保持卖出股票状态（状态二），这里其实从 「状态二」的定义来说 ，很难明确应该初始多少，这种情况我们就看递推公式需要我们给他初始成什么数值。
如果i为1，第1天买入股票，那么递归公式中需要计算 dp[i - 1][1] - prices[i] ，即 dp[0][1] - prices[1]，那么大家感受一下 dp[0][1] （即第0天的状态二）应该初始成多少，只能初始为0。想一想如果初始为其他数值，是我们第1天买入股票后 手里还剩的现金数量是不是就不对了。
今天卖出了股票（状态三），同上分析，dp[0][2]初始化为0，dp[0][3]也初始为0。
4.确定遍历顺序
从递归公式上可以看出，dp[i] 依赖于 dp[i-1]，所以是从前向后遍历。
5.举例推导dp数组1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
if (n == 0) return 0;
vector<vector<int>> dp(n, vector<int>(4, 0));
dp[0][0] -= prices[0]; // 持股票
for (int i = 1; i < n; i++) {
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]));
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];
}
return max(dp[n - 1][3], max(dp[n - 1][1], dp[n - 1][2]));
}
};
买卖股票的最佳时机含手续费
给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格 ；整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。
dp[i][0] 表示第i天持有股票所得最多现金。 dp[i][1] 表示第i天不持有股票所得最多现金
如果第i天持有股票即dp[i][0]， 那么可以由两个状态推出来
- 第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金 即：dp[i - 1][0]
- 第i天买入股票，所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即：dp[i - 1][1] - prices[i]
所以：dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
在来看看如果第i天不持有股票即dp[i][1]的情况， 依然可以由两个状态推出来
- 第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金 即：dp[i - 1][1]
- 第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金，注意这里需要有手续费了即：dp[i - 1][0] + prices[i] - fee
所以：dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n = prices.size();
// dp数组含义
// dp[i][j]表示第i天持有或者不持有股票的最大利润
vector<vector<int>> dp(n,vector<int>(2));
// 卖出股票时减去手续费
// j=0表示不持有
//初始化
dp[0][1] = -prices[0];
for(int i =1;i<n;++i) {
dp[i][0] = max(dp[i-1][0],dp[i-1][1]+prices[i]-fee);
dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i]);
}
return max(dp[n-1][1],dp[n-1][0]);
}
};
本题和动态规划：122.买卖股票的最佳时机II 的区别就是这里需要多一个减去手续费的操作
最长递增子序列
给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
子序列问题是动态规划解决的经典问题，当前下标i的递增子序列长度，其实和i之前的下标j的子序列长度有关系，那又是什么样的关系呢。
用动规五部曲来详细分析：
- dp[i]的定义
本题中，正确定义dp数组的含义十分重要。dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度为什么一定表示 “以nums[i]结尾的最长递增子序” ，因为在做递增比较的时候，如果比较 nums[j] 和 nums[i] 的大小，那么两个递增子序列一定分别以nums[j]为结尾 和 nums[i]为结尾， 要不然这个比较就没有意义了，不是尾部元素的比较那么如何算递增呢。
2.状态转移方程
位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。
所以：if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
注意这里不是要dp[i] 与 dp[j] + 1进行比较，而是要取dp[j] + 1的最大值。
3.dp[i]的初始化
每一个i，对应的dp[i]（即最长递增子序列）起始大小至少都是1.
4.确定遍历顺序
dp[i] 是有0到i-1各个位置的最长递增子序列 推导而来，那么遍历i一定是从前向后遍历。
j其实就是遍历0到i-1，那么是从前到后，还是从后到前遍历都无所谓，只要吧 0 到 i-1 的元素都遍历了就行了。 所以默认习惯 从前向后遍历
5.举例推导dp数组1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
// dp[n] 表示以索引i结尾的数组的最长递增长度
if(nums.empty()) {
return 0;
}
int sz = nums.size();
vector<int> dp(sz,1);
int max_len{1};
for(int i = 1;i<sz;++i) {
for(int j = 0;j<i;j++) {
if(nums.at(i)>nums.at(j)) {
dp[i] = max(dp[i],dp[j]+1);
}
}
max_len = max(max_len,dp[i]);
}
return max_len;
}
};
本题最关键的是要想到dp[i]由哪些状态可以推出来，并取最大值，那么很自然就能想到递推公式：dp[i] = max(dp[i], dp[j] + 1);
最长严格递增序列
给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
// 滑动窗口
// int maxLen{1};
// int n = nums.size();
// int cnt{1};
// for (int i = 1; i < n; ++i) {
// if (nums[i] > nums[i - 1]) {
// cnt++;
// maxLen = max(maxLen, cnt);
// } else {
// // 重新计数
// cnt = 1;
// }
// }
// return maxLen;
// 动态规划
int n = nums.size();
// 含义 以nums[i]结尾的最长连续递增序列
vector<int> dp(n,1);
int result{1};
for(int i = 1;i<n;++i) {
if(nums[i]>nums[i-1]) {
dp[i] = dp[i-1]+1;
}
result = max(result,dp[i]);
}
return result;
}
};
不连续递增子序列的跟前0-i 个状态有关，连续递增的子序列只跟前一个状态有关.关键在递推公式和遍历方法上
最长重复子数组
给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度
注意题目中说的子数组，其实就是连续子序列。本题其实是动规解决的经典题目，我们只要想到 用二维数组可以记录两个字符串的所有比较情况，这样就比较好推 递推公式了
- 确定dp数组（dp table）以及下标的含义
dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。 （特别注意： “以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 ）
2.确定递推公式
根据dp[i][j]的定义，dp[i][j]的状态只能由dp[i - 1][j - 1]推导出来。
即当A[i - 1] 和B[j - 1]相等的时候，dp[i][j] = dp[i - 1][j - 1] + 1;
3.dp数组如何初始化
根据dp[i][j]的定义，dp[i][0] 和dp[0][j]其实都是没有意义的！
但dp[i][0] 和dp[0][j]要初始值，因为 为了方便递归公式dp[i][j] = dp[i - 1][j - 1] + 1;
所以dp[i][0] 和dp[0][j]初始化为0。
4.确定遍历顺序
外层for循环遍历A，内层for循环遍历B。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2) {
int n1 = nums1.size();
int n2 = nums2.size();
// 含义 dp[i][j]表示以nums1[i]和nums2[j]结尾的重复最长子数组长度
vector<vector<int>> dp(n1+1,vector<int>(1+n2));
// 状态转移方程
// dp[i][j] =
// nums[i] == nums[j]? 1+dp[i-1][j-1]:max(dp[i-1][j],dp[i][j-1])
// dp初始化
int maxLen{INT_MIN};
for(int i = 1;i<=n1;i++) {
for(int j = 1;j<=n2;j++) {
if(nums1[i-1] == nums2[j-1]) {
dp[i][j] = dp[i-1][j-1]+1;
}
maxLen = max(maxLen,dp[i][j]);
}
}
return maxLen;
}
};
最长公共子序列
给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。
一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
- 例如，
"ace"是"abcde"的子序列，但"aec"不是"abcde"的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
动规五部曲分析如下：
- 确定dp数组（dp table）以及下标的含义
dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]
2.确定递推公式
主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同
如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;
如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。
3.dp数组如何初始化
text1[0, i-1]和空串的最长公共子序列自然是0，所以dp[i][0] = 0;
- 遍历顺序
- 举例推导
1 | class Solution { |
不相交的线
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足：
nums1[i] == nums2[j]- 且绘制的直线不与任何其他连线（非水平线）相交。
请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。
以这种方法绘制线条，并返回可以绘制的最大连线数。
绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，只要 nums1[i] == nums2[j]，且直线不能相交
直线不能相交，这就是说明在字符串nums1中 找到一个与字符串nums2相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，连接相同数字的直线就不会相交。
其实也就是说nums1和nums2的最长公共子序列是[1,4]，长度为2。 这个公共子序列指的是相对顺序不变（即数字4在字符串nums1中数字1的后面，那么数字4也应该在字符串nums2数字1的后面）
本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
// dp数组含义
int n1 = nums1.size();
int n2 = nums2.size();
// dp[i][j]表示以[0-i-1]的nums1和[0-j-1]nums2序列最多的连线数
vector<vector<int>> dp(n1 + 1, vector<int>(n2 + 1));
// 状态转移方程
// dp[i][j] = dp[i-1]
for (int i = 1; i <= n1; ++i) {
for (int j = 1; j <= n2; ++j) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
}
}
}
return dp[n1][n2];
}
};
最大子数组和
给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。子数组是数组中的一个连续部分1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
int maxSubArray(vector<int>& nums) {
// 贪心
// 当累加和小于当前值时,重新开始累加
int preSum{};
int maxResult{INT_MIN};
for (int i = 0; i < nums.size(); ++i) {
preSum += nums[i];
if (preSum < nums[i]) {
preSum = nums[i];
}
// preSum = max(preSum+nums[i],nums[i]);
maxResult = max(maxResult,preSum);
}
return maxResult;
}
};
动规五部曲如下：
- 确定dp数组（dp table）以及下标的含义
dp[i]：包括下标i（以nums[i]为结尾）的最大连续子序列和为dp[i]。
2.确定递推公式
dp[i]只有两个方向可以推出来：
- dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
- nums[i]，即：从头开始计算当前连续子序列和
一定是取最大的，所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);
3.dp数组如何初始化
从递推公式可以看出来dp[i]是依赖于dp[i - 1]的状态，dp[0]就是递推公式的基础。
dp[0]应该是多少呢?
根据dp[i]的定义，很明显dp[0]应为nums[0]即dp[0] = nums[0]。
4.确定遍历顺序
递推公式中dp[i]依赖于dp[i - 1]的状态，需要从前向后遍历。
5.举例推导dp数组1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
int maxSubArray(vector<int>& nums) {
if (nums.size() == 0) return 0;
vector<int> dp(nums.size());
dp[0] = nums[0];
int result = dp[0];
for (int i = 1; i < nums.size(); i++) {
dp[i] = max(dp[i - 1] + nums[i], nums[i]); // 状态转移公式
if (dp[i] > result) result = dp[i]; // result 保存dp[i]的最大值
}
return result;
}
};
判断子序列
给定字符串 s 和 t ，判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。
编辑距离的入门题目，因为从题意中也可以发现，只需要计算删除的情况，不用考虑增加和替换的情况。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
bool isSubsequence(string s, string t) {
// 问题转化
// s与t的最长公共子序列是否是s
int n1 = s.size();
int n2 = t.size();
// [0-i-1]的字符串s与[0-j-1]的字符串t的最长公共子序列长度
vector<vector<int>> dp(n1 + 1, vector<int>(n2 + 1));
for (int i = 1; i <= n1; ++i) {
for (int j = 1; j <= n2; ++j) {
if (s[i - 1] == t[j - 1]) {
dp[i][j] = 1 + dp[i - 1][j - 1];
} else {
dp[i][j] = dp[i][j - 1];
}
}
}
return dp[n1][n2] == s.size();
双指针1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
bool isSubsequence(string s, string t) {
int n1 = s.size(),n2 = t.size();
// 双指针
int i{},j{};
for(int j = 0;j<n2;++j) {
if(s[i] == t[j]) {
i++;
}
}
if(i == n1) {
return true;
}
return false;
}
};
不同的子序列
给你两个字符串 s 和 t ，统计并返回在 s 的 子序列 中 t 出现的个数。测试用例保证结果在 32 位有符号整数范围内。
这道题目如果不是子序列，而是要求连续序列的，那就可以考虑用KMP1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
int numDistinct(string s, string t) {
int n1 = s.size();
int n2 = t.size();
//[0-i]的字符串s的子序列中出现以t[j-1]的个数
// dp[i][j]以i-1结尾的子序列中包含以j结尾的字符串t的个数
vector<vector<uint64_t>> dp(n1 + 1, vector<uint64_t>(n2 + 1));
// 从s中删除一些元素得到t
// 需要初始化dp[0][j]和dp[i][0]
for (int i = 0; i <= n1; i++) {
dp[i][0] = 1;
}
for (int i = 1; i <= n1; ++i) {
for (int j = 1; j <= n2; ++j) {
if (s[i - 1] == t[j - 1]) {
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[s.size()][t.size()];
}
};
定义一个 dp[i][j]，表示 s 的前 i 个字符构成的子串中，包含 t 的前 j 个字符构成的子序列的个数。
- 定义状态
dp[i][j]：s[0...i-1] 中包含 t[0...j-1] 子序列的个数。
- 状态转移方程
对于 dp[i][j]，有两种情况：
如果
s[i-1]!=t[j-1]： 当前s的字符与t的字符不匹配，所以s的第i个字符无法用来匹配t的第j个字符。因此，我们只能从s的前i-1个字符中寻找t的前j个子序列，所以：dp[i][j]=dp[i−1][j]
如果
s[i-1]==t[j-1]： 当前s的字符与t的字符匹配，有两种选择：不使用
s[i-1]：我们从s的前i-1个字符中寻找t的前j个子序列，个数为dp[i-1][j]。使用
s[i-1]：我们用s[i-1]来匹配t[j-1]，然后从s的前i-1个字符中寻找t的前j-1个子序列，个数为dp[i-1][j-1]。 因此，总数是两者的和：dp[i][j]=dp[i−1][j]+dp[i−1][j−1]
综合起来，状态转移方程为：
dp[i][j]={dp[i−1][j]dp[i−1][j]+dp[i−1][j−1]if s[i−1]=t[j−1]if s[i−1]=t[j−1]
- 初始化
dp[i][0]= 1：s的任意前i个字符中，包含空字符串t（前 0 个字符）的子序列的个数都为 1（即空子序列）。dp[0][j]= 0：空字符串s无法包含任何非空字符串t。dp[0][0]= 1：空字符串s包含空字符串t的个数为 1。
两个字符串的删除操作
给定两个单词 word1 和 word2 ，返回使得 word1 和 word2 相同所需的最小步数。
每步 可以删除任意一个字符串中的一个字符。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
int minDistance(string word1, string word2) {
int n1 = word1.size();
int n2 = word2.size();
// 将以i-1结尾的字符串word1转为以j-1结尾的字符串word2
vector<vector<int>> dp(n1+1,vector<int>(n2+1));
// 初始化
for(int i =0;i<=n1;i++) {
dp[i][0] = i;
}
for(int j = 0;j<=n2;j++) {
dp[0][j] = j;
}
for(int i = 1;i<=n1;++i) {
for(int j = 1;j<=n2;++j) {
if(word1[i-1] == word2[j-1]) {
dp[i][j] = dp[i-1][j-1];
}else{
dp[i][j] = min(dp[i-1][j]+1,dp[i][j-1]+1);
}
}
}
return dp[n1][n2];
}
};
编辑距离
给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作：
- 插入一个字符
- 删除一个字符
- 替换一个字符
- 确定dp数组（dp table）以及下标的含义
dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]
- 确定递推公式
在确定递推公式的时候，首先要考虑清楚编辑的几种操作
if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑，dp[i][j] 就应该是 dp[i - 1][j - 1]，即dp[i][j] = dp[i - 1][j - 1];
此时可能有同学有点不明白，为啥要即dp[i][j] = dp[i - 1][j - 1]呢？
那么就在回顾上面讲过的dp[i][j]的定义，word1[i - 1] 与 word2[j - 1]相等了，那么就不用编辑了，以下标i-2为结尾的字符串word1和以下标j-2为结尾的字符串word2的最近编辑距离dp[i - 1][j - 1]就是 dp[i][j]了。
在下面的讲解中，如果哪里看不懂，就回想一下dp[i][j]的定义，就明白了。
在整个动规的过程中，最为关键就是正确理解dp[i][j]的定义！
if (word1[i - 1] != word2[j - 1])，此时就需要编辑了，如何编辑呢？
- 操作一：word1删除一个元素，那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i - 1][j] + 1;
- 操作二：word2删除一个元素，那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i][j - 1] + 1;
这里有同学发现了，怎么都是删除元素，添加元素去哪了。
word2添加一个元素，相当于word1删除一个元素，例如 word1 = "ad" ，word2 = "a"，word1删除元素'd' 和 word2添加一个元素'd'，变成word1="a", word2="ad"， 最终的操作数是一样
操作三：替换元素，word1替换word1[i - 1]，使其与word2[j - 1]相同，此时不用增删加元素。
可以回顾一下，if (word1[i - 1] == word2[j - 1])的时候我们的操作 是 dp[i][j] = dp[i - 1][j - 1] 对吧。
那么只需要一次替换的操作，就可以让 word1[i - 1] 和 word2[j - 1] 相同。
所以 dp[i][j] = dp[i - 1][j - 1] + 1;
综上，当 if (word1[i - 1] != word2[j - 1]) 时取最小的，即：dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
- dp数组如何初始化
再回顾一下dp[i][j]的定义：
dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。
那么dp[i][0] 和 dp[0][j] 表示什么呢？
dp[i][0] ：以下标i-1为结尾的字符串word1，和空字符串word2，最近编辑距离为dp[i][0]。
那么dp[i][0]就应该是i，对word1里的元素全部做删除操作，即：dp[i][0] = i;
同理dp[0][j] = j;
- 确定遍历顺序
从如下四个递推公式：
dp[i][j] = dp[i - 1][j - 1]dp[i][j] = dp[i - 1][j - 1] + 1dp[i][j] = dp[i][j - 1] + 1dp[i][j] = dp[i - 1][j] + 1
可以看出dp[i][j]是依赖左方，上方和左上方元素的1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 /class Solution {
public:
int minDistance(string word1, string word2) {
int n1 = word1.size();
int n2 = word2.size();
// 以i-1结尾的字符串转w1为以j-1结尾的字符串w2的最少操作数
vector<vector<int>> dp(n1 + 1, vector<int>(n2+1));
// 初始化
for (int i = 0; i <= n1; ++i) {
dp[i][0] = i;
}
for (int i = 0; i <= n2; ++i) {
dp[0][i] = i;
}
for(int i = 1;i<=n1;++i) {
for(int j = 1;j<=n2;++j) {
if(word1[i-1] == word2[j-1]) {
dp[i][j] = dp[i-1][j-1];
}else{
dp[i][j] = min(min(1+dp[i-1][j],1+dp[i][j-1]),1+dp[i-1][j-1]);
}
}
}
return dp[n1][n2];
}
};
回文子串
给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19int countSubstrings(string s) {
int sz = s.size();
vector<vector<bool>> dp(sz, vector<bool>(sz, false));
int counts{};
// dp[i][j] 表示[i,j]字串是否是回文
for (int i = sz - 1; i >= 0; --i) {
for (int j = i; j < sz; j++) {
if (i == j) {
dp[i][j] = true;
} else if (i == j - 1) {
dp[i][j] = s[i] == s[j];
} else {
dp[i][j] = (s[i] == s[j]) && dp[i + 1][j - 1];
}
counts += dp[i][j] ? 1 : 0;
}
}
return counts;
}
另外还可以使用字符串中以i或者以i,i+1间隔迭代计算回文字串数目. 双指针法
动态规划的空间复杂度是偏高的，再看一下双指针法。
首先确定回文串，就是找中心然后向两边扩散看是不是对称的就可以了。
在遍历中心点的时候，要注意中心点有两种情况。一个元素可以作为中心点，两个元素也可以作为中心点。
在计算的时候，要注意一个元素为中心点和两个元素为中心点的情况。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int countSubstrings(string s) {
int result = 0;
for (int i = 0; i < s.size(); i++) {
result += extend(s, i, i, s.size()); // 以i为中心
result += extend(s, i, i + 1, s.size()); // 以i和i+1为中心
}
return result;
}
int extend(const string& s, int i, int j, int n) {
int res = 0;
while (i >= 0 && j < n && s[i] == s[j]) {
i--;
j++;
res++;
}
return res;
}
};
最长回文子串
给你一个字符串 s，找到 s 中最长的 回文 子串。
- 定义状态
我们定义一个二维布尔数组 dp[i][j]，其中 dp[i][j] 表示从索引 i 到索引 j 的子串 s[i...j] 是否是回文子串。
- 状态转移方程
要确定 dp[i][j] 的值，我们需要考虑以下条件：
- 如果
s[i]!=s[j]： 首尾字符不相等，那么s[i...j]肯定不是回文，所以dp[i][j] = false。 - 如果
s[i]==s[j]： 首尾字符相等，我们还需要看中间的子串s[i+1...j-1]是否是回文。- 如果
s[i+1...j-1]是回文，那么s[i...j]也是回文。 - 此时，状态转移方程为
dp[i][j] = dp[i+1][j-1]。
- 如果
边界条件： 对于长度为 1 或 2 的子串，我们需要单独处理：
- 长度为 1：
dp[i][i] = true。单个字符总是回文。 - 长度为 2：
dp[i][i+1] = (s[i] == s[i+1])。
- 遍历顺序
我们需要保证在计算 dp[i][j] 时，dp[i+1][j-1] 的值已经被计算过。
- 如果我们从左到右、从上到下遍历，
dp[i+1][j-1]依赖于j-1，而j在j-1后面，这会导致依赖错误。 - 正确的遍历顺序应该是：
- 从子串长度从小到大遍历。
- 对于每个长度，从左到右遍历起始位置
i。
- 记录最长回文子串
在填充 dp 数组的过程中，每当 dp[i][j] 被设置为 true 时，我们都检查一下当前子串 s[i...j] 的长度 (j - i + 1) 是否大于已知的最长回文子串的长度。如果是，就更新最长回文子串。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
// dp[i][j]表示[i,j]的子串是否是回文子串
vector<vector<bool>> dp(n, vector<bool>(n));
// 状态转移方程
// 初始化
for (int i = 0; i < n; ++i) {
dp[i][i] = true;
}
int maxLen = 1;
int start = 0;
// 遍历子串长度
for (int len = 2; len <= n; len++) {
// 遍历起始位置
for (int i = 0; i <= n - len; i++) {
int j = i + len - 1;
if (s[i] != s[j]) {
dp[i][j] = false;
} else {
if (len <= 3) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1];
}
}
if (dp[i][j] && len > maxLen) {
maxLen = len;
start = i;
}
}
}
return s.substr(start, maxLen);
}
};
最长回文子序列
给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。
子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。
一种方法是将原本字符串与逆序后的字符串求最长公共字串长度.
另外可以直接使用动态规划.
可以使用一个二维 DP 数组来解决这个问题。定义 dp[i][j] 为字符串 s 在索引 i 到 j 之间的子串中，最长回文子序列的长度
状态转移方程
要计算 dp[i][j]，我们需要考虑子串 s[i...j] 的两端字符 s[i] 和 s[j]：
- 如果
s[i] == s[j]这意味着这两个字符可以作为回文子序列的一部分。此时，最长回文子序列的长度是在s[i+1...j-1]子串的最长回文子序列的基础上，加上这两个匹配的字符。dp[i][j] = dp[i+1][j-1] + 2 - 如果
s[i] != s[j]这两个字符不匹配，我们不能同时将它们都作为回文子序列的一部分。因此，我们需要在以下两种情况中取最大值：s[i...j-1]子串中的最长回文子序列的长度 (dp[i][j-1])。s[i+1...j]子串中的最长回文子序列的长度 (dp[i+1][j])。dp[i][j] = max(dp[i][j-1], dp[i+1][j])
边界条件
需要初始化 DP 数组。当子串的长度为 1 时，它本身就是一个回文子序列，所以：
dp[i][i] = 1
遍历顺序
观察状态转移方程，dp[i][j] 依赖于 dp[i+1][j-1]、dp[i][j-1] 和 dp[i+1][j]。这意味着在计算 dp[i][j] 时，我们需要先知道其左下角、左边和下边的值。
为了满足这个依赖关系，我们应该从小到大遍历子串的长度，然后从后往前遍历起始索引。
- 外层循环：子串长度
len从 1 到n。 - 内层循环：起始索引
i从n-1到 0。 - 结束索引
j总是i + len - 1。
1 | class Solution { |
乘积最大子数组
给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续 子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution {
public:
int maxProduct(vector<int>& nums) {
int n = nums.size();
// 以i结尾的数组的子数组的乘积最大值
// 空间压缩
int max_ = nums[0];
int min_ = nums[0];
int result{nums[0]};
for (int i = 1; i < n; ++i) {
int temp = max_;
max_ = max(nums[i], max(nums[i] * max_, min_ * nums[i]));
min_ = min(nums[i], min(nums[i] * temp, min_ * nums[i]));
result = max(result,max_);
}
return result;
// vector<vector<int>> dp(n,vector<int>(2));
// int result{nums[0]};
// // 初始化
// dp[0][0] = nums[0];
// dp[0][1] = nums[0];
// for(int i = 1;i<n;++i) {
// dp[i][0] =
// max(nums[i],max(dp[i-1][0]*nums[i],dp[i-1][1]*nums[i])); dp[i][1]
// = min(nums[i],min(dp[i-1][0]*nums[i],dp[i-1][1]*nums[i])); result
// = max(dp[i][0],result);
// }
// return result;
}
};
最长有效括号
给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号 子串 的长度。
左右括号匹配，即每个左括号都有对应的右括号将其闭合的字符串是格式正确的，比如 "(()())"
二叉树
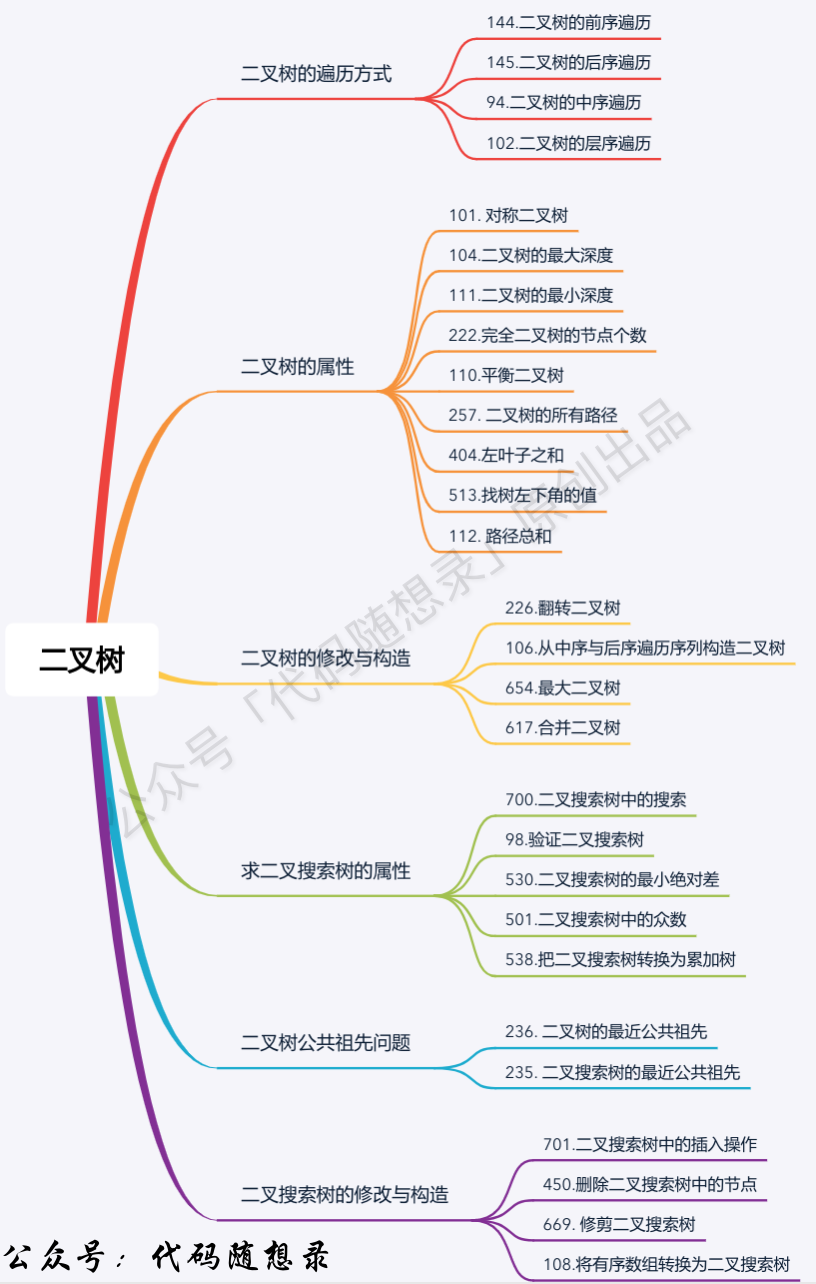
二叉树类型
满二叉树,如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。深度为k，有2^k-1个节点的二叉树
完全二叉树,除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（h从1开始），则该层包含 1~ 2^(h-1) 个节点。
优先级队列其实是一个堆，堆就是一棵完全二叉树，同时保证父子节点的顺序关系。
二叉搜索树是一个有序树:
- 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
- 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
- 它的左、右子树也分别为二叉排序树
平衡二叉搜索树,它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
二叉树存储
二叉树可以链表式存储也可以数组顺序存储,每个节点最多有两个子节点1
2
3
4
5
6struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
数组来存储二叉树如何遍历,如果根节点为0,如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2,一个节点的父节点为(i-1)/2
二叉树遍历方式
二叉树主要有两种遍历方式：
- 深度优先遍历：先往深走，遇到叶子节点再往回走。
- 广度优先遍历：一层一层的去遍历。
从深度优先遍历和广度优先遍历进一步拓展，才有如下遍历方式：
- 深度优先遍历
- 前序遍历
- 中序遍历
- 后序遍历
- 广度优先遍历
- 层次遍历
三种递归方式实现
每次写递归，都按照这三要素来写
- 确定递归函数的参数和返回值： 确定哪些参数是递归的过程中需要处理的，那么就在递归函数里加上这个参数， 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
- 确定终止条件： 写完了递归算法, 运行的时候，经常会遇到栈溢出的错误，就是没写终止条件或者终止条件写的不对，操作系统也是用一个栈的结构来保存每一层递归的信息，如果递归没有终止，操作系统的内存栈必然就会溢出。
- 确定单层递归的逻辑： 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
1 | class Solution { |
中序遍历1
2
3
4
5
6void traversal(TreeNode* cur, vector<int>& vec) {
if (cur == NULL) return;
traversal(cur->left, vec); // 左
vec.push_back(cur->val); // 中
traversal(cur->right, vec); // 右
}
后序遍历1
2
3
4
5
6void traversal(TreeNode* cur, vector<int>& vec) {
if (cur == NULL) return;
traversal(cur->left, vec); // 左
traversal(cur->right, vec); // 右
vec.push_back(cur->val); // 中
}
三种栈遍历方式的实现
递归的实现就是：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。
用栈实现 DFS 的核心思想是：
- 将根节点压入栈中。
- 进入一个循环，只要栈不为空，就执行以下操作：
- 弹出栈顶节点，并访问它。
- 将该节点的右子节点压入栈中（如果存在）。
- 将该节点的左子节点压入栈中（如果存在）。
为什么先压入右子节点，再压入左子节点？因为栈是后进先出（LIFO）的。这样做可以确保左子节点总是先于右子节点被弹出和访问，从而模拟了递归的深度优先探索顺序。
使用栈实现 DFS 可以轻松模拟前序、中序和后序遍历。
- 前序遍历（Pre-order Traversal）
前序遍历的顺序是：根 -> 左 -> 右。使用栈实现时，只需按照核心思想的步骤即可。
- 步骤：
- 将根节点入栈。
- 循环直到栈为空：
- 弹出节点
node，访问它。 - 将
node的右子节点入栈（如果存在）。 - 将
node的左子节点入栈（如果存在）。
- 弹出节点
1 |
|
- 中序遍历（In-order Traversal）
中序遍历的顺序是：左 -> 根 -> 右。这个实现稍复杂，因为我们需要在访问根节点之前，先遍历完它的所有左子节点。前序遍历的逻辑无法直接应用到中序遍历上。
在迭代的过程中，其实有两个操作：
- 处理：将元素放进result数组中
- 访问：遍历节点
因为前序遍历的顺序是中左右，先访问的元素是中间节点，要处理的元素也是中间节点，所以刚刚才能写出相对简洁的代码，因为要访问的元素和要处理的元素顺序是一致的，都是中间节点。
再看看中序遍历，中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进result数组中），这就造成了处理顺序和访问顺序是不一致的。那么在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素.
- 步骤：
- 初始化一个
current指针指向根节点。 - 循环直到
current为空且栈为空：- 将所有左子节点依次入栈，直到
current为空。 - 弹出栈顶节点
node，访问它。 - 让
current指向node的右子节点，继续循环。
- 将所有左子节点依次入栈，直到
- 初始化一个
1 | std::vector<int> inorderTraversal(TreeNode* root) { |
- 后序遍历（Post-order Traversal）
后序遍历的顺序是：左 -> 右 -> 根。这是三种遍历中最复杂的。一种常见的技巧是：
- 先用类似前序遍历的方式，以根 -> 右 -> 左的顺序遍历。
- 将遍历结果存入一个临时数组。
- 最后将临时数组反转，即可得到后序遍历的结果。
- 步骤：
- 将根节点入栈。
- 循环直到栈为空：
- 弹出节点
node，将它的值存入临时数组。 - 将
node的左子节点入栈（如果存在）。 - 将
node的右子节点入栈（如果存在）。
- 弹出节点
- 反转临时数组。
1 | std::vector<int> postorderTraversal(TreeNode* root) { |
前序和中序是完全两种代码风格，并不像递归写法那样代码稍做调整，就可以实现前后中序。这是因为前序遍历中访问节点（遍历节点）和处理节点（将元素放进result数组中）可以同步处理，但是中序就无法做到同步. 但也有使用栈统一处理先/中/后序遍历二叉树的方法代码随想录
- 方法一：就是要处理的节点放入栈之后，紧接着放入一个空指针作为标记。 这种方法可以叫做
空指针标记法。 - 方法二：加一个
boolean值跟随每个节点，false(默认值) 表示需要为该节点和它的左右儿子安排在栈中的位次，true表示该节点的位次之前已经安排过了，可以收割节点了。 这种方法可以叫做boolean 标记法，样例代码见下文C++ 和 Python 的 boolean 标记法。 这种方法更容易理解，在面试中更容易写出来。
三种栈遍历方式统一实现
1 | class Solution { |
1 | class Solution { |
1 | class Solution { |
二叉树的层序遍历
层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。
需要借用一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑，而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。而这种层序遍历方式就是图论中的广度优先遍历，只不过我们应用在二叉树上. 层序遍历模板1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
vector<vector<int>> result;
while (!que.empty()) {
int size = que.size();
vector<int> vec;
// 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
result.push_back(vec);
}
return result;
}
};
二叉树的右视图
给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。
层序遍历的时候，判断是否遍历到单层的最后面的元素，如果是，就放进result数组中，随后返回result就可以了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
public:
// void bfs(TreeNode* root,vector<int>& r) {
// r.push_back(root->val);
// if(root->right) {
// bfs(root->right,r);
// }else if(root->left) {
// bfs(root->left,r);
// }
// }
vector<int> rightSideView(TreeNode* root) {
// 层序遍历 找到每一层最有一个节点
// 每一层先添加右节点
if (!root) {
return {};
}
vector<int> r;
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
int sz = q.size();
int i = 0;
while (sz--) {
auto t = q.front();
q.pop();
if (i == 0) {
r.push_back(t->val);
}
i++;
// 加入右子树
if (t->right) {
q.push(t->right);
}
if (t->left) {
q.push(t->left);
}
}
}
return r;
}
};
填充每个节点的下一个右侧结点指针
给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：1
2
3
4
5
6struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。
初始状态下，所有 next 指针都被设置为 NULL。
在单层遍历的时候记录一下本层的头部节点，然后在遍历的时候让前一个节点指向本节点就可以了1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node* next;
Node() : val(0), left(NULL), right(NULL), next(NULL) {}
Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
Node(int _val, Node* _left, Node* _right, Node* _next)
: val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
Node* connect(Node* root) {
// 层次遍历 在每一层指向下一个节点
if (!root) {
return nullptr;
}
queue<Node*> q;
q.push(root);
while (!q.empty()) {
int sz = q.size();
Node* prev = nullptr;
for (int i = 0; i < sz; ++i) {
auto t = q.front();
q.pop();
if (t->left) {
q.push(t->left);
}
if (t->right) {
q.push(t->right);
}
if (prev != nullptr) {
prev->next = t;
}
prev = t;
}
}
return root;
}
};
二叉树的最大深度
给定一个二叉树 root ，返回其最大深度。二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37class Solution {
public:
int maxDepth1(TreeNode* root) {
// 二叉树问题 递归 dfs bfs
//递归
if(root == nullptr) {
return 0;
}
return max(maxDepth1(root->left),maxDepth1(root->right))+1;
}
int maxDepth(TreeNode* root) {
if(root == nullptr) {
return 0;
}
queue<TreeNode*> q_node;
q_node.push(root);
int depth{};
while(!q_node.empty()) {
int sz = q_node.size();
depth++;
while(sz--) {
auto node = q_node.front();
if(node->left) {
q_node.push(node->left);
}
if(node->right) {
q_node.push(node->right);
}
q_node.pop();
}
}
return depth;
}
};
二叉树的最小深度
给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明：叶子节点是指没有子节点的节点。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32class Solution {
public:
int minDepth(TreeNode* root) {
if (!root) {
return 0;
}
queue<TreeNode*> q;
q.push(root);
int depth{};
while (!q.empty()) {
int sz = q.size();
depth++;
while (sz--) {
auto t = q.front();
if (t->left == nullptr && t->right == nullptr) {
return depth;
}
q.pop();
if (t->left) {
q.push(t->left);
}
if (t->left) {
q.push(t->left);
}
if (t->right) {
q.push(t->right);
}
}
}
return depth;
}
};
二叉树的递归
几乎所有的二叉树递归问题，都可以归纳为下面这三个步骤。这是一种自顶向下、分而治之的思考方式。
确定递归函数的作用（What does this function do?） 这是最重要的一步。在写代码之前，你需要清晰地定义你的函数是做什么的。
- 比如，对于翻转二叉树，你的函数
invertTree(root)的作用就是：给定一个节点root，它会返回一个以root为根的、已经翻转过的二叉树。 - 比如，对于求最大深度，你的函数
maxDepth(root)的作用就是：给定一个节点root，它会返回以root为根的子树的最大深度。
一旦你明确了函数的作用，接下来的步骤就变得顺理成章。
- 比如，对于翻转二叉树，你的函数
确定递归的终止条件（When does it stop?） 这是递归的“安全网”，也是所有递归必须有的出口。
- 对于二叉树问题，最基本的终止条件就是：当节点为空时（
root == nullptr）。 - 如果
root是空节点，那么就没有子树，也没有任何操作可做。这时通常返回nullptr（对于翻转）或0（对于求深度）。
- 对于二叉树问题，最基本的终止条件就是：当节点为空时（
确定本次递归要做什么（What does it do this time?） 这一步是核心的逻辑。它利用了我们第一步定义的“函数作用”，将大问题分解为小问题。
- 翻转二叉树：
- 你的任务是翻转以
root为根的树。 - 根据第一步，我们知道
invertTree函数能够翻转一个子树。 - 所以，我们只需要调用
invertTree(root->left)和invertTree(root->right)来分别翻转它的左右子树。 - 然后，把翻转后的左右子树交换位置：
swap(root->left, root->right)。 - 最后，返回根节点
root。
- 你的任务是翻转以
- 求最大深度：
- 你的任务是求以
root为根的树的最大深度。 - 根据第一步，我们知道
maxDepth函数能够求一个子树的最大深度。 - 所以，我们只需要调用
maxDepth(root->left)和maxDepth(root->right)来分别获取左右子树的深度。 - 然后，将这两个深度中的最大值加 1（加上当前节点这一层）就是最终结果：
max(maxDepth(root->left), maxDepth(root->right)) + 1。
- 你的任务是求以
掌握这种“三步法”思维模式后，你会发现很多二叉树问题都是相同的套路：
- 定义函数要做什么。
- 写好终止条件。
- 利用函数本身处理子问题，然后将子问题的结果合并或处理，得到当前层的结果。
类似的二叉树递归题，比如“判断是否为平衡二叉树”、“求二叉树的直径”、“判断是否为对称二叉树”等等
- 翻转二叉树：
翻转二叉树
给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。
想要翻转它，其实就把每一个节点的左右孩子交换一下就可以了,关键在于遍历顺序，前中后序应该选哪一种遍历顺序？ （一些同学这道题都过了，但是不知道自己用的是什么顺序）
遍历的过程中去翻转每一个节点的左右孩子就可以达到整体翻转的效果。
注意只要把每一个节点的左右孩子翻转一下，就可以达到整体翻转的效果
这道题目使用前序遍历和后序遍历都可以，唯独中序遍历不方便，因为中序遍历会把某些节点的左右孩子翻转了两次！建议拿纸画一画，就理解了
也可以使用层序遍历,只要把每一个节点的左右孩子翻转一下的遍历方式都是可以的1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root == nullptr) {
return nullptr;
}
swap(root->left,root->right);
invertTree(root->right);
invertTree(root->left);
return root;
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if (root == nullptr) {
return nullptr;
}
stack<TreeNode*> stk;
stk.push(root);
while (!stk.empty()) {
auto t = stk.top();
stk.pop();
swap(t->left, t->right);
if (t->left) {
stk.push(t->left);
}
if (t->right) {
stk.push(t->right);
}
}
return root;
}
};
从根节点开始，递归地对树进行遍历，并从叶子节点先开始翻转。如果当前遍历到的节点 root 的左右两棵子树都已经翻转，那么我们只需要交换两棵子树的位置，即可完成以 root 为根节点的整棵子树的翻转。1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if (root == nullptr) {
return nullptr;
}
TreeNode* left = invertTree(root->left);
TreeNode* right = invertTree(root->right);
root->left = right;
root->right = left;
return root;}
};
也可以用广度优先1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
swap(node->left, node->right); // 节点处理
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return root;
}
};
对称二叉树
给你一个二叉树的根节点 root ， 检查它是否轴对称
既可以使用递归也可以迭代
递归三部曲
- 确定递归函数的参数和返回值
因为我们要比较的是根节点的两个子树是否是相互翻转的，进而判断这个树是不是对称树，所以要比较的是两个树，参数自然也是左子树节点和右子树节点。
- 确定终止条件
要比较两个节点数值相不相同，首先要把两个节点为空的情况弄清楚,否则后面比较数值的时候就会操作空指针了.节点为空的情况有：
- 左节点为空，右节点不为空，不对称，return false
- 左不为空，右为空，不对称 return false
- 左右都为空，对称，返回true
此时已经排除掉了节点为空的情况，那么剩下的就是左右节点不为空：
- 左右都不为空，比较节点数值，不相同就return false
此时左右节点不为空，且数值也不相同的情况我们也处理了。
- 确定单层递归的逻辑
此时才进入单层递归的逻辑，单层递归的逻辑就是处理 左右节点都不为空，且数值相同的情况。
- 比较二叉树外侧是否对称：传入的是左节点的左孩子，右节点的右孩子。
- 比较内侧是否对称，传入左节点的右孩子，右节点的左孩子。
- 如果左右都对称就返回true ，有一侧不对称就返回false 。
1 | class Solution { |
迭代法,可以使用队列或者栈,将两棵树的左右节点压入然后取出进行比较.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56class Solution {
public:
bool isSymmetric(TreeNode* root) {
if (root == nullptr) {
return true;
}
// return isNodeSyn(root->left, root->right);
queue<TreeNode*> q;
q.push(root->left);
q.push(root->right);
while (!q.empty()) {
auto n1 = q.front();
q.pop();
auto n2 = q.front();
q.pop();
if (!n1 && !n2) {
return true;
}
if (!n1 || !n2 || n1->val != n2->val) {
return false;
}
// 继续压入数据
q.push(n1->left);
q.push(n2->right);
q.push(n1->right);
q.push(n2->left);
}
return true;
}
};
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
stack<TreeNode*> st; // 这里改成了栈
st.push(root->left);
st.push(root->right);
while (!st.empty()) {
TreeNode* rightNode = st.top(); st.pop();
TreeNode* leftNode = st.top(); st.pop();
if (!leftNode && !rightNode) {
continue;
}
if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
return false;
}
st.push(leftNode->left);
st.push(rightNode->right);
st.push(leftNode->right);
st.push(rightNode->left);
}
return true;
}
};
使用栈也是类似的,主要是存储子节点的作用
完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。
完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（从第 0 层开始），则该层包含 1~ 2h 个节点
完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。
对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。
对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算.如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。
这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢？
在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树.在完全二叉树中，如果递归向左遍历的深度不等于递归向右遍历的深度，则说明不是满二叉树1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
public:
int countNodes(TreeNode* root) {
// 将完全二叉树分成多个满二叉树
// 在完全二叉树中 左遍历深度==右遍历深度 则为完全二叉树
// 利用公式算节点数目
if (!root) { // 终止条件
return 0;
}
// 递归逻辑
int leftDepth{}, rightDepth{};
TreeNode* left = root->left;
while (left) {
left = left->left;
leftDepth++;
}
TreeNode* right = root->right;
while (right) {
rightDepth++;
right = right->right;
}
if(leftDepth == rightDepth) {
return (2<<leftDepth)-1;
}
return 1+countNodes(root->left)+countNodes(root->right);
}
};
递归三部曲中第一部函数参数和返回值,函数作用是计算root为根节点的完全二叉树的节点数.
判断其子树是不是满二叉树，如果是则利用公式计算这个子树（满二叉树）的节点数量，如果不是则继续递归，那么在递归三部曲中，第二部：终止条件的写法
递归三部曲，第三部，单层递归的逻辑：（可以看出使用后序遍历）1
2
3
4int leftTreeNum = countNodes(root->left); // 左
int rightTreeNum = countNodes(root->right); // 右
int result = leftTreeNum + rightTreeNum + 1; // 中
return result;
平衡二叉树
给定一个二叉树，判断它是否是 平衡二叉树1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int computeDepth(TreeNode* node) {
if(!node) {
return 0;
}
int leftDepth = computeDepth(node->left);
int rightDepth = computeDepth(node->right);
if(leftDepth == -1 || rightDepth == -1) {
// 左子树或者右子树不是平衡二叉树
return -1;
}
if(abs(leftDepth-rightDepth)>1) {
return -1; // 该根节点的二叉树不是平衡二叉树
}
return 1+max(leftDepth,rightDepth);
}
bool isBalanced(TreeNode* root) {
return computeDepth(root)!=-1;
}
};
递归三步曲分析：
- 明确递归函数的参数和返回值
参数：当前传入节点。 返回值：以当前传入节点为根节点的树的高度。
那么如何标记左右子树是否差值大于1呢？如果当前传入节点为根节点的二叉树已经不是二叉平衡树了，还返回高度的话就没有意义了。所以如果已经不是二叉平衡树了，可以返回-1 来标记已经不符合平衡树的规则了。
- 明确终止条件
递归的过程中依然是遇到空节点了为终止，返回0，表示当前节点为根节点的树高度为03.明确单层递归的逻辑
- 如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢？当然是其左子树高度和其右子树高度的差值。分别求出其左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则返回-1，表示已经不是二叉平衡树了。
1 | class Solution { |
二叉树的所有路径
给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
要求从根节点到叶子的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径。在这道题目中将第一次涉及到回溯，因为我们要把路径记录下来，需要回溯来回退一个路径再进入另一个路径。
先使用递归的方式，来做前序遍历。递归和回溯就是一家的，本题也需要回溯1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59// 版本一
class Solution {
private:
void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {
path.push_back(cur->val); // 中，中为什么写在这里，因为最后一个节点也要加入到path中
// 这才到了叶子节点
if (cur->left == NULL && cur->right == NULL) {
string sPath;
for (int i = 0; i < path.size() - 1; i++) {
sPath += to_string(path[i]);
sPath += "->";
}
sPath += to_string(path[path.size() - 1]);
result.push_back(sPath);
return;
}
if (cur->left) { // 左
traversal(cur->left, path, result);
path.pop_back(); // 回溯
}
if (cur->right) { // 右
traversal(cur->right, path, result);
path.pop_back(); // 回溯
}
}
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
vector<int> path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};
class Solution {
private:
void traversal(TreeNode* cur, string path, vector<string>& result) {
path += to_string(cur->val); // 中
if (cur->left == NULL && cur->right == NULL) {
result.push_back(path);
return;
}
if (cur->left) traversal(cur->left, path + "->", result); // 左
if (cur->right) traversal(cur->right, path + "->", result); // 右
}
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
string path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};
注意在函数定义的时候void traversal(TreeNode* cur, string path, vector<string>& result) ，定义的是string path，每次都是复制赋值，不用使用引用，否则就无法做到回溯的效果。
那么在如上代码中，貌似没有看到回溯的逻辑，其实不然，回溯就隐藏在traversal(cur->left, path + "->", result);中的 path + "->"。 每次函数调用完，path依然是没有加上”->” 的，这就是回溯了。
还可以使用栈模拟,这里除了模拟递归需要一个栈，同时还需要一个栈来存放对应的遍历路径。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
public:
vector<string> binaryTreePaths(TreeNode* root) {
stack<TreeNode*> treeSt;// 保存树的遍历节点
stack<string> pathSt; // 保存遍历路径的节点
vector<string> result; // 保存最终路径集合
if (root == NULL) return result;
treeSt.push(root);
pathSt.push(to_string(root->val));
while (!treeSt.empty()) {
TreeNode* node = treeSt.top(); treeSt.pop(); // 取出节点 中
string path = pathSt.top();pathSt.pop(); // 取出该节点对应的路径
if (node->left == NULL && node->right == NULL) { // 遇到叶子节点
result.push_back(path);
}
if (node->right) { // 右
treeSt.push(node->right);
pathSt.push(path + "->" + to_string(node->right->val));
}
if (node->left) { // 左
treeSt.push(node->left);
pathSt.push(path + "->" + to_string(node->left->val));
}
}
return result;
}
};
相同的树
给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
// 递归 使用栈 遍历顺序
// 递归参数和返回值
if (!p && !q) {
return true;
}
if ((p == nullptr && q) || (p && q == nullptr)) {
return false;
}
// 递归结束条件
// 单层递归函数 先序遍历
return (p->val == q->val) && isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
// 递归 使用栈 遍历顺序
// 递归参数和返回值
stack<TreeNode*> stk;
stk.push(p);
stk.push(q);
while (!stk.empty()) {
auto n1 = stk.top();
stk.pop();
auto n2 = stk.top();
stk.pop();
if (n1 == nullptr && n2 || n1 && n2 == nullptr) {
return false;
}
if (n1 == nullptr && n2 == nullptr) {
continue;
}
if (n1->val != n2->val) {
return false;
}
stk.push(n1->left);
stk.push(n2->left);
stk.push(n1->right);
stk.push(n2->right);
}
return true;
}
};
虽然理论上所有的递归都可以用迭代来实现，但是有的场景难度可能比较大。
例如：都知道回溯法其实就是递归，但是很少人用迭代的方式去实现回溯算法,讲了这么多二叉树题目的迭代法，有的同学会疑惑，迭代法中究竟什么时候用队列，什么时候用栈？
如果是模拟前中后序遍历就用栈，如果是适合层序遍历就用队列，当然还是其他情况，那么就是 先用队列试试行不行，不行就用栈
另一颗树的子树
1 | class Solution { |
深度优先搜索序列上做串匹配
这个方法需要我们先了解一个「小套路」：一棵子树上的点在深度优先搜索序列（即先序遍历）中是连续的。了解了这个「小套路」之后，我们可以确定解决这个问题的方向就是：把 s 和 t 先转换成深度优先搜索序列，然后看 t 的深度优先搜索序列是否是 s 的深度优先搜索序列的「子串」。
这样做正确吗？ 假设 s 由两个点组成，1 是根，2 是 1 的左孩子；t 也由两个点组成，1 是根，2 是 1 的右孩子。这样一来 s 和 t 的深度优先搜索序列相同，可是 t 并不是 s 的某一棵子树。由此可见「s 的深度优先搜索序列包含 t 的深度优先搜索序列」是「t 是 s 子树」的必要不充分条件，所以单纯这样做是不正确的。
为了解决这个问题，我们可以引入两个空值 lNull 和 rNull，当一个节点的左孩子或者右孩子为空的时候，就插入这两个空值，这样深度优先搜索序列就唯一对应一棵树。处理完之后，就可以通过判断「s 的深度优先搜索序列包含 t 的深度优先搜索序列」来判断答案
用 KMP 判断的代码实现1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70class Solution {
public:
vector <int> sOrder, tOrder;
int maxElement, lNull, rNull;
void getMaxElement(TreeNode *o) {
if (!o) {
return;
}
maxElement = max(maxElement, o->val);
getMaxElement(o->left);
getMaxElement(o->right);
}
void getDfsOrder(TreeNode *o, vector <int> &tar) {
if (!o) {
return;
}
tar.push_back(o->val);
if (o->left) {
getDfsOrder(o->left, tar);
} else {
tar.push_back(lNull);
}
if (o->right) {
getDfsOrder(o->right, tar);
} else {
tar.push_back(rNull);
}
}
bool kmp() {
int sLen = sOrder.size(), tLen = tOrder.size();
vector <int> fail(tOrder.size(), -1);
for (int i = 1, j = -1; i < tLen; ++i) {
while (j != -1 && tOrder[i] != tOrder[j + 1]) {
j = fail[j];
}
if (tOrder[i] == tOrder[j + 1]) {
++j;
}
fail[i] = j;
}
for (int i = 0, j = -1; i < sLen; ++i) {
while (j != -1 && sOrder[i] != tOrder[j + 1]) {
j = fail[j];
}
if (sOrder[i] == tOrder[j + 1]) {
++j;
}
if (j == tLen - 1) {
return true;
}
}
return false;
}
bool isSubtree(TreeNode* s, TreeNode* t) {
maxElement = INT_MIN;
getMaxElement(s);
getMaxElement(t);
lNull = maxElement + 1;
rNull = maxElement + 2;
getDfsOrder(s, sOrder);
getDfsOrder(t, tOrder);
return kmp();
}
};
最大深度的多种解法
给定一个二叉树，找出其最大深度. 既可以使用递归也可以使用迭代. 迭代就是用队列广搜.
递归可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。
- 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
- 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始）
根节点的高度就是二叉树的最大深度，所以通过后序求的根节点高度来求的二叉树最大深度。
先用后序遍历（左右中）来计算树的高度。
- 确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型。
2.确定终止条件：如果为空节点的话，就返回0，表示高度为0。
- 确定单层递归的逻辑：先求它的左子树的深度，再求右子树的深度，最后取左右深度最大的数值 再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。
1 | class Solution { |
使用前序1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int result;
void getdepth(TreeNode* node, int depth) {
result = depth > result ? depth : result; // 中
if (node->left == NULL && node->right == NULL) return ;
if (node->left) { // 左
getdepth(node->left, depth + 1);
}
if (node->right) { // 右
getdepth(node->right, depth + 1);
}
return ;
}
int maxDepth(TreeNode* root) {
result = 0;
if (root == 0) return result;
getdepth(root, 1);
return result;
}
};
最小深度的多种解法
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。也可以使用递归或者迭代1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
int getDepth(TreeNode* node) {
if (node == NULL) return 0;
int leftDepth = getDepth(node->left); // 左
int rightDepth = getDepth(node->right); // 右
// 中
// 当一个左子树为空，右不为空，这时并不是最低点
if (node->left == NULL && node->right != NULL) {
return 1 + rightDepth;
}
// 当一个右子树为空，左不为空，这时并不是最低点
if (node->left != NULL && node->right == NULL) {
return 1 + leftDepth;
}
int result = 1 + min(leftDepth, rightDepth);
return result;
}
int minDepth(TreeNode* root) {
return getDepth(root);
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31lass Solution {
private:
int result;
void getdepth(TreeNode* node, int depth) {
// 函数递归终止条件
if (node == nullptr) {
return;
}
// 中，处理逻辑：判断是不是叶子结点
if (node -> left == nullptr && node->right == nullptr) {
result = min(result, depth);
}
if (node->left) { // 左
getdepth(node->left, depth + 1);
}
if (node->right) { // 右
getdepth(node->right, depth + 1);
}
return ;
}
public:
int minDepth(TreeNode* root) {
if (root == nullptr) {
return 0;
}
result = INT_MAX;
getdepth(root, 1);
return result;
}
};
左叶子之和
给定二叉树的根节点 root ，返回所有左叶子之和。
递归的遍历顺序为后序遍历（左右中），是因为要通过递归函数的返回值来累加求取左叶子数值之和。
递归三部曲：
- 确定递归函数的参数和返回值
判断一个树的左叶子节点之和，那么一定要传入树的根节点，递归函数的返回值为数值之和，所以为int
使用题目中给出的函数就可以了。
- 确定终止条件
如果遍历到空节点，那么左叶子值一定是01
if (root == NULL) return 0;
注意，只有当前遍历的节点是父节点，才能判断其子节点是不是左叶子。 所以如果当前遍历的节点是叶子节点，那其左叶子也必定是0，那么终止条件为：1
2if (root == NULL) return 0;
if (root->left == NULL && root->right== NULL) return 0; //其实这个也可以不写，如果不写不影响结果，但就会让递归多进行了一层。
- 确定单层递归的逻辑
当遇到左叶子节点的时候，记录数值，然后通过递归求取左子树左叶子之和，和 右子树左叶子之和，相加便是整个树的左叶子之和。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
// 递归
if (!root) {
return 0; // 结束条件
}
int sum{};
if (root->left && (root->left->left == nullptr) && (root->left->right == nullptr)) {
sum = root->left->val;
}
int leftSum = sumOfLeftLeaves(root->left);
int rightSum = sumOfLeftLeaves(root->right);
return sum + leftSum + rightSum;
}
};
迭代法使用前中后序都是可以的，只要把左叶子节点统计出来，就可以
找树左下角的值
给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29class Solution {
public:
int maxDepth = INT_MIN;
int result;
void traversal(TreeNode* root, int depth) {
if (root->left == NULL && root->right == NULL) {
if (depth > maxDepth) {
maxDepth = depth;
result = root->val;
}
return;
}
if (root->left) {
depth++;
traversal(root->left, depth);
depth--; // 回溯
}
if (root->right) {
depth++;
traversal(root->right, depth);
depth--; // 回溯
}
return;
}
int findBottomLeftValue(TreeNode* root) {
traversal(root, 0);
return result;
}
};
或者使用队列1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21// // bfs队列
queue<TreeNode*> q;
q.push(root);
int result{};
while (!q.empty()) {
int sz = q.size();
for (int i = 0; i < sz; ++i) {
auto n = q.front();
q.pop();
if (i == 0) {
result = n->val;
}
if(n->left) {
q.push(n->left);
}
if(n->right) {
q.push(n->right);
}
}
}
return result;
路径总和
给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。说明: 叶子节点是指没有子节点的节点。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if(root == nullptr) {
return false;
}
if(root->left == nullptr && root->right == nullptr) {
if(targetSum == root->val) {
return true;
}else{
return false;
}
}
return hasPathSum(root->left,targetSum-root->val) || hasPathSum(root->right,targetSum-root->val);
}
};
可以使用递归,可以使用深度优先遍历的方式来遍历二叉树
- 确定递归函数的参数和返回类型
参数：需要二叉树的根节点，还需要一个计数器，这个计数器用来计算二叉树的一条边之和是否正好是目标和，计数器为int型。
再来看返回值，递归函数什么时候需要返回值？什么时候不需要返回值？这里总结如下三点：
- 如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。
- 如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。
- 如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。
- 确定终止条件
首先计数器如何统计这一条路径的和呢？
不要去累加然后判断是否等于目标和，那么代码比较麻烦，可以用递减，让计数器count初始为目标和，然后每次减去遍历路径节点上的数值。
如果最后count == 0，同时到了叶子节点的话，说明找到了目标和。
如果遍历到了叶子节点，count不为0，就是没找到。
- 确定单层递归的逻辑
因为终止条件是判断叶子节点，所以递归的过程中就不要让空节点进入递归了。
递归函数是有返回值的，如果递归函数返回true，说明找到了合适的路径，应该立刻返回。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
private:
bool traversal(TreeNode* cur, int count) {
if (!cur->left && !cur->right && count == 0) return true; // 遇到叶子节点，并且计数为0
if (!cur->left && !cur->right) return false; // 遇到叶子节点直接返回
if (cur->left) { // 左
count -= cur->left->val; // 递归，处理节点;
if (traversal(cur->left, count)) return true;
count += cur->left->val; // 回溯，撤销处理结果
}
if (cur->right) { // 右
count -= cur->right->val; // 递归，处理节点;
if (traversal(cur->right, count)) return true;
count += cur->right->val; // 回溯，撤销处理结果
}
return false;
}
public:
bool hasPathSum(TreeNode* root, int sum) {
if (root == NULL) return false;
return traversal(root, sum - root->val);
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
bool dfs(TreeNode* node, int count) {
if (node->left == nullptr && node->right == nullptr && count == 0) {
return true;
}
if (!node->left && !node->right)
return false;
bool left{}, right{};
if (node->left) {
left = dfs(node->left, count - node->left->val);
}
if (node->right) {
right = dfs(node->right, count - node->right->val);
}
return left || right;
}
bool hasPathSum(TreeNode* root, int targetSum) {
if (root == nullptr) {
return false;
}
return dfs(root, targetSum - root->val);}};
路径总和II
给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。叶子节点 是指没有子节点的节点1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution {
public:
void backtrace(TreeNode* node, vector<int>& path,
vector<vector<int>>& result, int targetSum) {
// 截止条件
if (node->left == nullptr && node->right == nullptr) {
if (targetSum == node->val) {
path.push_back(node->val);
result.push_back(path);
path.pop_back();
}
return;
}
if (node->left) {
path.push_back(node->val);
backtrace(node->left, path, result, targetSum - node->val);
path.pop_back();
}
if(node->right){
path.push_back(node->val);
backtrace(node->right, path, result, targetSum - node->val);
path.pop_back();
}
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
if (!root) {
return {};
}
vector<vector<int>> result;
vector<int> path;
backtrace(root, path, result, targetSum);
return result;
}
};
要遍历整个树，找到所有路径，所以递归函数不要返回值！1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40class solution {
private:
vector<vector<int>> result;
vector<int> path;
// 递归函数不需要返回值，因为我们要遍历整个树
void traversal(TreeNode* cur, int count) {
if (!cur->left && !cur->right && count == 0) { // 遇到了叶子节点且找到了和为sum的路径
result.push_back(path);
return;
}
if (!cur->left && !cur->right) return ; // 遇到叶子节点而没有找到合适的边，直接返回
if (cur->left) { // 左 （空节点不遍历）
path.push_back(cur->left->val);
count -= cur->left->val;
traversal(cur->left, count); // 递归
count += cur->left->val; // 回溯
path.pop_back(); // 回溯
}
if (cur->right) { // 右 （空节点不遍历）
path.push_back(cur->right->val);
count -= cur->right->val;
traversal(cur->right, count); // 递归
count += cur->right->val; // 回溯
path.pop_back(); // 回溯
}
return ;
}
public:
vector<vector<int>> pathSum(TreeNode* root, int sum) {
result.clear();
path.clear();
if (root == NULL) return result;
path.push_back(root->val); // 把根节点放进路径
traversal(root, sum - root->val);
return result;
}
};
从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。
以后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来再切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。
如果让我们肉眼看两个序列，画一棵二叉树的话，应该分分钟都可以画出来
说到一层一层切割，就应该想到了递归。
来看一下一共分几步：
- 第一步：如果数组大小为零的话，说明是空节点了。
- 第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
- 第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
- 第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）
- 第五步：切割后序数组，切成后序左数组和后序右数组
- 第六步：递归处理左区间和右区间
1 | class Solution { |
从中序和先序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
TreeNode* construct(const vector<int>& preorder,
const unordered_map<int, int>& inmap, int inbegin,
int inend, int prebegin, int preend) {
if (inbegin >= inend || prebegin >= preend) {
return nullptr;
}
int root_val = preorder.at(prebegin); // 拿到头节点值
int mid_idx = inmap.at(root_val); // 获得在中序中的位置 分割
TreeNode* root = new TreeNode(root_val);
int leftNodeNum = mid_idx - inbegin;
root->left = construct(preorder, inmap, inbegin, mid_idx,
prebegin + 1, prebegin+leftNodeNum+1);
root->right = construct(preorder, inmap,mid_idx+1, inend,
prebegin+leftNodeNum+1, preend);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if (preorder.empty() || inorder.empty()) {
return nullptr;
}
unordered_map<int, int> inmap;
for (int i = 0; i < inorder.size(); ++i) {
inmap[inorder[i]] = i;
}
return construct(preorder, inmap, 0, inorder.size(), 0, preorder.size());
}
};
前序和中序可以唯一确定一棵二叉树.后序和中序可以唯一确定一棵二叉树.前序和后序不能唯一确定一棵二叉树.因为没有中序遍历无法确定左右部分，也就是无法分割
最大二叉树
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点，其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树\ 。
注意类似用数组构造二叉树的题目，每次分隔尽量不要定义新的数组，而是通过下标索引直接在原数组上操作，这样可以节约时间和空间上的开销。
递归函数什么时候加if，什么时候不加if，其实就是控制空节点（空指针）是否进入递归，是不同的代码实现方式，都是可以的。
一般情况来说：如果让空节点（空指针）进入递归，就不加if，如果不让空节点进入递归，就加if限制一下， 终止条件也会相应的调整1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
TreeNode* construct(vector<int>& nums, int left, int right) {
if (left > right) {
return nullptr;
}
int maxValueIndex = left;
int maxVal = nums[maxValueIndex];
for (int i = left + 1; i <= right; ++i) {
// maxVal = max(maxVal, nums[i]); // 找到最大值
if(nums[i]>maxVal) {
maxVal = nums[i];
maxValueIndex = i;
}
}
TreeNode* root = new TreeNode(maxVal);
root->left = construct(nums, left , maxValueIndex - 1);
root->right = construct(nums, maxValueIndex + 1, right);
return root;
}
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
return construct(nums, 0, nums.size() - 1);
}
};
还可以使用单调栈,可以将题目中构造树的过程等价转换为下面的构造过程：
初始时，我们只有一个根节点，其中存储了整个数组；
在每一步操作中，我们可以「任选」一个存储了超过一个数的节点，找出其中的最大值并存储在该节点。最大值左侧的数组部分下放到该节点的左子节点，右侧的数组部分下放到该节点的右子节点；
如果所有的节点都恰好存储了一个数，那么构造结束。
由于最终构造出的是一棵树，因此无需按照题目的要求「递归」地进行构造，而是每次可以「任选」一个节点进行构造。这里可以类比一棵树的「深度优先搜索」和「广度优先搜索」，二者都可以起到遍历整棵树的效果。
既然可以任意进行选择，那么我们不妨每次选择数组中最大值最大的那个节点进行构造。这样一来，我们就可以保证按照数组中元素降序排序的顺序依次构造每个节点。因此：
当我们选择的节点中数组的最大值为 nums[i] 时，所有大于 nums[i] 的元素已经被构造过（即被单独放入某一个节点中），所有小于 nums[i] 的元素还没有被构造过。
这就说明：在最终构造出的树上，以 nums[i] 为根节点的子树，在原数组中对应的区间，左边界为 nums[i] 左侧第一个比它大的元素所在的位置，右边界为 nums[i] 右侧第一个比它大的元素所在的位置。左右边界均为开边界。如果某一侧边界不存在，则那一侧边界为数组的边界。如果两侧边界均不存在，说明其为最大值，即根节点。并且：nums[i] 的父结点是两个边界中较小的那个元素对应的节点。
单调栈构建最大二叉树
1 | class Solution { //单调栈 |
任务变为：找出每一个元素左侧和右侧第一个比它大的元素所在的位置。这就是一个经典的单调栈问题了。如果左侧的元素较小，那么该元素就是左侧元素的右子节点；如果右侧的元素较小，那么该元素就是右侧元素的左子节点。
合并二叉树
给你两棵二叉树： root1 和 root2 。
想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。注意: 合并过程必须从两个树的根节点开始
- 确定递归函数的参数和返回值：
首先要合入两个二叉树，那么参数至少是要传入两个二叉树的根节点，返回值就是合并之后二叉树的根节点。
2.确定终止条件：
因为是传入了两个树，那么就有两个树遍历的节点t1 和 t2，如果t1 == NULL 了，两个树合并就应该是 t2 了（如果t2也为NULL也无所谓，合并之后就是NULL）。反过来如果t2 == NULL，那么两个数合并就是t1
3.确定单层递归的逻辑：
单层递归的逻辑就比较好写了，这里我们重复利用一下t1这个树，t1就是合并之后树的根节点（就是修改了原来树的结构）。
单层递归中，就要把两棵树的元素加到一起。接下来t1 的左子树是：合并 t1左子树 t2左子树之后的左子树。t1 的右子树：是 合并 t1右子树 t2右子树之后的右子树。
最终t1就是合并之后的根节点。1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
TreeNode* merge(TreeNode* node1, TreeNode* node2) {
if(!node1) return node2;
if(!node2) return node1;
node1->val += node2->val;
node1->left = merge(node1->left, node2->left);
node1->right = merge(node1->right, node2->right);
return node1;
}
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
return merge(root1, root2);
}
};
也可以使用队列,迭代法中，一般一起操作两个树都是使用队列模拟类似层序遍历，同时处理两个树的节点，这种方式最好理解，如果用模拟递归的思路的话，要复杂一些。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if (t1 == NULL) return t2;
if (t2 == NULL) return t1;
queue<TreeNode*> que;
que.push(t1);
que.push(t2);
while(!que.empty()) {
TreeNode* node1 = que.front(); que.pop();
TreeNode* node2 = que.front(); que.pop();
// 此时两个节点一定不为空，val相加
node1->val += node2->val;
// 如果两棵树左节点都不为空，加入队列
if (node1->left != NULL && node2->left != NULL) {
que.push(node1->left);
que.push(node2->left);
}
// 如果两棵树右节点都不为空，加入队列
if (node1->right != NULL && node2->right != NULL) {
que.push(node1->right);
que.push(node2->right);
}
// 当t1的左节点 为空 t2左节点不为空，就赋值过去
if (node1->left == NULL && node2->left != NULL) {
node1->left = node2->left;
}
// 当t1的右节点 为空 t2右节点不为空，就赋值过去
if (node1->right == NULL && node2->right != NULL) {
node1->right = node2->right;
}
}
return t1;
}
};
二叉搜索树中的搜索
二叉搜索树是一个有序树：
- 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
- 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
- 它的左、右子树也分别为二叉搜索树
1 | class Solution { |
二叉搜索树的遍历方式因为二叉搜索树的有序性，遍历的时候要比普通二叉树简单很多。
二叉树遍历的迭代法，可能立刻想起使用栈来模拟深度遍历，使用队列来模拟广度遍历。
对于二叉搜索树可就不一样了，因为二叉搜索树的特殊性，也就是节点的有序性，可以不使用辅助栈或者队列就可以写出迭代法。对于一般二叉树，递归过程中还有回溯的过程，例如走一个左方向的分支走到头了，那么要调头，在走右分支。而对于二叉搜索树，不需要回溯的过程，因为节点的有序性就帮我们确定了搜索的方向。1
2
3
4
5
6
7
8
9
10class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
if (root == NULL || root->val == val) return root;
TreeNode* result = NULL;
if (root->val > val) result = searchBST(root->left, val);
if (root->val < val) result = searchBST(root->right, val);
return result;
}
};
验证二叉搜索树
给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下：
- 节点的左子树只包含 严格小于 当前节点的数。
- 节点的右子树只包含 严格大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树
1 | class Solution { |
把二叉树转变为数组来判断，是最直观的，但其实不用转变成数组，可以在递归遍历的过程中直接判断是否有序。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32class Solution {
public:
bool isValidBST(TreeNode* root) {
// 中序遍历
if (!root) {
return true;
}
stack<TreeNode*> stk;
int prev{};
TreeNode* cur = root;
bool firstNode{true};
while (cur || !stk.empty()) {
while (cur) {
stk.push(cur);
cur = cur->left;
}
// 中间节点
cur = stk.top();
stk.pop();
if (firstNode) {
firstNode = false;
} else {
if (cur->val <= prev) {
return false;
}
}
prev = cur->val;
cur = cur->right;
}
return true;
}
};
也可以使用指针指向前一个节点,为空表示第一个节点.取到最左面节点的数值来比较。1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
TreeNode* pre = NULL; // 用来记录前一个节点
bool isValidBST(TreeNode* root) {
if (root == NULL) return true;
bool left = isValidBST(root->left);
if (pre != NULL && pre->val >= root->val) return false;
pre = root; // 记录前一个节点
bool right = isValidBST(root->right);
return left && right;
}
};
- 陷阱1
不能单纯的比较左节点小于中间节点，右节点大于中间节点就完事了
- 陷阱2
样例中最小节点 可能是int的最小值，如果这样使用最小的int来比较也是不行的
在二叉搜索树上求什么最值，求差值之类的，都要思考一下二叉搜索树可是有序的，要利用好这一特点。同时要学会在递归遍历的过程中如何记录前后两个指针，这也是一个小技巧
二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。
回溯法自底向上查找,后序遍历。 如何判断一个节点是节点q和节点p的公共祖先1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
TreeNode* dfs(TreeNode* node, TreeNode* p, TreeNode* q) {
if (node == nullptr || node->val == p->val || q->val == node->val) {
return node;
}
TreeNode* left = dfs(node->left, p, q);
TreeNode* right = dfs(node->right, p, q);
if (left && right) {
return node;
}
if (!left) {
return right;
}
return left;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (!root) {
return nullptr;
}
return dfs(root, p, q);
}
};
在递归函数有返回值的情况下：如果要搜索一条边，递归函数返回值不为空的时候，立刻返回，如果搜索整个树，直接用一个变量left、right接住返回值，这个left、right后序还有逻辑处理的需要，也就是后序遍历中处理中间节点的逻辑（也是回溯）
二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。
从上向下去递归遍历，第一次遇到 cur节点是数值在[q, p]区间中，那么cur就是 q和p的最近公共祖先。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (!root) {
return nullptr;
}
if (root->val < p->val && root->val < q->val) {
TreeNode* r = lowestCommonAncestor(root->right, p, q);
if (r) {
return r;
}
}
if (root->val > p->val && root->val > q->val) {
TreeNode* l = lowestCommonAncestor(root->left, p, q);
if (l) {
return l;
}
}
return root;
}
};
二叉搜索树的插入
给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。
注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
// 遍历找到非叶子节点进行插入
if (!root) {
TreeNode* node = new TreeNode(val);
return node;
}
if (root->val > val) {
// 插入左子树
root->left = insertIntoBST(root->left, val);
}
if (root->val < val) {
root->right = insertIntoBST(root->right, val);
}
return root;
}
};
也可以通过迭代法,就是记录父节点,比较大小.然后插入到父节点的子节点1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(root == nullptr) {
TreeNode* node = new TreeNode(val);
return node;
}
TreeNode* parent = root;
TreeNode* cur = root;
while(cur) {
parent = cur;
if(cur->val>val) {
cur = cur->left;
}else{
cur = cur->right;
}
}
if(parent->val>val) {
parent->left = new TreeNode(val);
}else{
parent->right = new TreeNode(val);
}
return root;
删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。
一般来说，删除节点可分为两个步骤：
- 首先找到需要删除的节点；
- 如果找到了，删除它。
1 | class Solution { |
1 | class Solution { |
修剪二叉搜索树
给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。
- 确定递归函数的参数以及返回值
这里我们为什么需要返回值呢？
因为是要遍历整棵树，有返回值，更方便，可以通过递归函数的返回值来移除节点。
- 确定终止条件
修剪的操作并不是在终止条件上进行的，所以就是遇到空节点返回就可以了
- 确定单层递归的逻辑
如果root（当前节点）的元素小于low的数值，那么应该递归右子树，并返回右子树符合条件的头结点。如果root(当前节点)的元素大于high的，那么应该递归左子树，并返回左子树符合条件的头结点。
接下来要将下一层处理完左子树的结果赋给root->left，处理完右子树的结果赋给root->right。
最后返回root节点1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if (root == nullptr ) return nullptr;
if (root->val < low) {
TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点
return right;
}
if (root->val > high) {
TreeNode* left = trimBST(root->left, low, high); // 寻找符合区间[low, high]的节点
return left;
}
root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子
root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子
return root;
}
};
将有序数组转为二叉树
给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 平衡 二叉搜索树。
递归三部曲：
- 确定递归函数返回值及其参数
删除二叉树节点，增加二叉树节点，都是用递归函数的返回值来完成，这样是比较方便的
要构造二叉树，依然用递归函数的返回值来构造中节点的左右孩子。
- 确定递归终止条件
这里定义的是左闭右闭的区间，所以当区间 left > right的时候，就是空节点了。
- 确定单层递归的逻辑
首先取数组中间元素的位置，int mid = left + ((right - left) / 2);root的左孩子接住下一层左区间的构造节点，右孩子接住下一层右区间构造的节点1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
TreeNode* buildTree(vector<int>& nums,int l ,int r) {
if(l>r) {
return nullptr;
}
int mid = (r-l)/2+l;
int root_val = nums[mid];
TreeNode* node = new TreeNode(root_val);
node->left =buildTree(nums,l,mid-1);
node->right =buildTree(nums,mid+1,r);
return node;
}
TreeNode* sortedArrayToBST(vector<int>& nums) {
// 中间节点作为根节点,然后建树
// if(nums.empty()) {
// return nullptr;
// }
return buildTree(nums,0,nums.size()-1);
}
};
把二叉搜索树转换为累加树
给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下，二叉搜索树满足下列约束条件：
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
1 | class Solution { |
1 | class Solution { |
图
图做深搜广搜的时候注意在哪里判断选择结束条件,实在做选择的时候还是在从堆栈中取出数据的时候
1 | int counts{}; |
图的种类
有向图 无向图 加权有向图 连通图 连通分量
度: 无向图中有几条边连接该节点.在有向图中，每个节点有出度和入度。出度：从该节点出发的边的个数。入度：指向该节点边的个数。
连通性:在图中表示节点的连通情况.在无向图中，任何两个节点都是可以到达的，我们称之为连通图.
在有向图中，任何两个节点是可以相互到达的，我们称之为 强连通图。在无向图中的极大连通子图称之为该图的一个连通分量,在有向图中极大强连通子图称之为该图的强连通分量.
图的存储
邻接表 使用 数组 + 链表的方式来表示。 邻接表是从边的数量来表示图，有多少边 才会申请对应大小的链表.有多少边 邻接表才会申请多少个对应的链表节点。
邻接表的优点：
- 对于稀疏图的存储，只需要存储边，空间利用率高
- 遍历节点连接情况相对容易
缺点：
- 检查任意两个节点间是否存在边，效率相对低，需要 O(V)时间，V表示某节点连接其他节点的数量。
- 实现相对复杂，不易理解
邻接矩阵 使用二维数组来表示图结构。 邻接矩阵是从节点的角度来表示图，有多少节点就申请多大的二维数组
这种表达方式（邻接矩阵） 在边少，节点多的情况下，会导致申请过大的二维数组，造成空间浪费。
而且在寻找节点连接情况的时候，需要遍历整个矩阵，即 n * n 的时间复杂度，同样造成时间浪费。
邻接矩阵的优点：
- 表达方式简单，易于理解
- 检查任意两个顶点间是否存在边的操作非常快
- 适合稠密图，在边数接近顶点数平方的图中，邻接矩阵是一种空间效率较高的表示方法。
缺点：
- 遇到稀疏图，会导致申请过大的二维数组造成空间浪费 且遍历 边 的时候需要遍历整个n * n矩阵，造成时间浪费
dfs与bfs
1 | void dfs(参数) { |
- 确认递归函数，参数
1 | void dfs(参数) |
通常我们递归的时候，我们递归搜索需要了解哪些参数，其实也可以在写递归函数的时候，发现需要什么参数，再去补充就可以。
一般情况，深搜需要 二维数组数组结构保存所有路径，需要一维数组保存单一路径，这种保存结果的数组，可以定义一个全局变量，避免让我们的函数参数过多。
例如这样：1
2
3vector<vector<int>> result; // 保存符合条件的所有路径
vector<int> path; // 起点到终点的路径
void dfs (图，目前搜索的节点)
2.确认终止条件
终止条件很重要，很多同学写dfs的时候，之所以容易死循环，栈溢出等等这些问题，都是因为终止条件没有想清楚。1
2
3
4if (终止条件) {
存放结果;
return;
}
终止添加不仅是结束本层递归，同时也是我们收获结果的时候。
另外，其实很多dfs写法，没有写终止条件，其实终止条件写在了， 隐藏在下面dfs递归的逻辑里了，也就是不符合条件，直接不会向下递归。这里如果大家不理解的话，没关系，后面会有具体题目来讲解。3.处理目前搜索节点出发的路径
一般这里就是一个for循环的操作，去遍历 目前搜索节点 所能到的所有节点。1
2
3
4
5for (选择：本节点所连接的其他节点) {
处理节点;
dfs(图，选择的节点); // 递归
回溯，撤销处理结果
}
广搜（bfs）是一圈一圈的搜索过程，和深搜（dfs）是一条路跑到黑然后再回溯。
广搜的搜索方式就适合于解决两个点之间的最短路径问题。
因为广搜是从起点出发，以起始点为中心一圈一圈进行搜索，一旦遇到终点，记录之前走过的节点就是一条最短路。
当然，也有一些问题是广搜 和 深搜都可以解决的，例如岛屿问题，这类问题的特征就是不涉及具体的遍历方式，只要能把相邻且相同属性的节点标记上就行1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四个方向
// grid 是地图，也就是一个二维数组
// visited标记访问过的节点，不要重复访问
// x,y 表示开始搜索节点的下标
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<pair<int, int>> que; // 定义队列
que.push({x, y}); // 起始节点加入队列
visited[x][y] = true; // 只要加入队列，立刻标记为访问过的节点
while(!que.empty()) { // 开始遍历队列里的元素
pair<int ,int> cur = que.front(); que.pop(); // 从队列取元素
int curx = cur.first;
int cury = cur.second; // 当前节点坐标
for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1]; // 获取周边四个方向的坐标
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 坐标越界了，直接跳过
if (!visited[nextx][nexty]) { // 如果节点没被访问过
que.push({nextx, nexty}); // 队列添加该节点为下一轮要遍历的节点
visited[nextx][nexty] = true; // 只要加入队列立刻标记，避免重复访问
}
}
}
}
岛屿问题 深搜.广搜
岛屿数量 岛屿最大面积 孤岛的总面积 沉没孤岛
水流问题
现有一个 N × M 的矩阵，每个单元格包含一个数值，这个数值代表该位置的相对高度。矩阵的左边界和上边界被认为是第一组边界，而矩阵的右边界和下边界被视为第二组边界。
矩阵模拟了一个地形，当雨水落在上面时，水会根据地形的倾斜向低处流动，但只能从较高或等高的地点流向较低或等高并且相邻（上下左右方向）的地点。我们的目标是确定那些单元格，从这些单元格出发的水可以达到第一组边界和第二组边界。
反过来想，从第一组边界上的节点 逆流而上，将遍历过的节点都标记上。同样从第二组边界的边上节点 逆流而上，将遍历过的节点也标记上。然后两方都标记过的节点就是既可以流向第一组边界也可以流向第二组边界的节点1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
using namespace std;
int n, m;
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
if (visited[x][y]) return;
visited[x][y] = true;
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) continue;
if (grid[x][y] > grid[nextx][nexty]) continue; // 注意：这里是从低向高遍历
dfs (grid, visited, nextx, nexty);
}
return;
}
int main() {
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
// 标记从第一组边界上的节点出发，可以遍历的节点
vector<vector<bool>> firstBorder(n, vector<bool>(m, false));
// 标记从第一组边界上的节点出发，可以遍历的节点
vector<vector<bool>> secondBorder(n, vector<bool>(m, false));
// 从最上和最下行的节点出发，向高处遍历
for (int i = 0; i < n; i++) {
dfs (grid, firstBorder, i, 0); // 遍历最左列，接触第一组边界
dfs (grid, secondBorder, i, m - 1); // 遍历最右列，接触第二组边界
}
// 从最左和最右列的节点出发，向高处遍历
for (int j = 0; j < m; j++) {
dfs (grid, firstBorder, 0, j); // 遍历最上行，接触第一组边界
dfs (grid, secondBorder, n - 1, j); // 遍历最下行，接触第二组边界
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
// 如果这个节点，从第一组边界和第二组边界出发都遍历过，就是结果
if (firstBorder[i][j] && secondBorder[i][j]) cout << i << " " << j << endl;;
}
}
}
建造最大岛屿
给定一个由 1（陆地）和 0（水）组成的矩阵，你最多可以将矩阵中的一格水变为一块陆地，在执行了此操作之后，矩阵中最大的岛屿面积是多少。
岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿是被水包围，并且通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设矩阵外均被水包围。
只要用一次深搜把每个岛屿的面积记录下来就好。
第一步：一次遍历地图，得出各个岛屿的面积，并做编号记录。可以使用map记录，key为岛屿编号，value为岛屿面积
第二步：再遍历地图，遍历0的方格（因为要将0变成1），并统计该1（由0变成的1）周边岛屿面积，将其相邻面积相加在一起，遍历所有 0 之后，就可以得出 选一个0变成1 之后的最大面积。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
using namespace std;
static vector<vector<int>> dirs = {{0,1},{0,-1},{1,0},{-1,0}};
void dfs(vector<vector<int>>& graph,int i,int j,int n,int m,int key,int& counts) {
graph[i][j] = key;
counts++;
for(auto dir:dirs) {
int nx = dir[0]+i;
int ny = dir[1]+j;
if(nx<0 || nx>=n || ny<0 ||ny>=m || graph[nx][ny]!=1) {
continue;
}
dfs(graph,nx,ny,n,m,key,counts);
}
}
int main() {
int n,m;
cin>>n>>m;
vector<vector<int>> graph(n,vector<int>(m));
for(int i = 0;i<n;++i) {
for(int j = 0;j<m;++j) {
cin>>graph[i][j];
}
}
int maxArea{};
// 1.计算所有岛屿 dfs 记录岛屿和大小
int key = 2;
unordered_map<int,int> umap;// 岛屿key以及对应大小
for(int i = 0;i<n;++i) {
for(int j = 0;j<m;++j) {
if(graph[i][j] == 1) {
int counts{};
dfs(graph,i,j,n,m,key,counts);
umap[key] = counts;
maxArea = max(maxArea,counts);
key++;
}
}
}
// 2. 从0开始遍历 看四周是否有岛屿
unordered_set<int> visitedGrid;
for(int i = 0;i<n;++i) {
for(int j = 0;j<m;++j) {
if(graph[i][j] !=0) {
continue;
}
visitedGrid.clear();
int cnt{};
for(auto dir:dirs) {
int nx = dir[0]+i;
int ny = dir[1]+j;
if(nx<0 || nx>=n || ny<0 ||ny>=m || graph[nx][ny]==0) {
continue;
}
if(visitedGrid.count(graph[nx][ny])) {
continue;
}
if(umap.count(graph[nx][ny])) {
cnt += umap[graph[nx][ny]];
visitedGrid.insert(graph[nx][ny]);
}
}
maxArea = max(maxArea,cnt+1);
}
}
cout<<maxArea<<'\n';
return 0;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
using namespace std;
int n, m;
int count;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y, int mark) {
if (visited[x][y] || grid[x][y] == 0) return; // 终止条件：访问过的节点 或者 遇到海水
visited[x][y] = true; // 标记访问过
grid[x][y] = mark; // 给陆地标记新标签
count++;
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) continue; // 越界了，直接跳过
dfs(grid, visited, nextx, nexty, mark);
}
}
int main() {
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
vector<vector<bool>> visited(n, vector<bool>(m, false)); // 标记访问过的点
unordered_map<int ,int> gridNum;
int mark = 2; // 记录每个岛屿的编号
bool isAllGrid = true; // 标记是否整个地图都是陆地
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 0) isAllGrid = false;
if (!visited[i][j] && grid[i][j] == 1) {
count = 0;
dfs(grid, visited, i, j, mark); // 将与其链接的陆地都标记上 true
gridNum[mark] = count; // 记录每一个岛屿的面积
mark++; // 记录下一个岛屿编号
}
}
}
if (isAllGrid) {
cout << n * m << endl; // 如果都是陆地，返回全面积
return 0; // 结束程序
}
// 以下逻辑是根据添加陆地的位置，计算周边岛屿面积之和
int result = 0; // 记录最后结果
unordered_set<int> visitedGrid; // 标记访问过的岛屿
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
count = 1; // 记录连接之后的岛屿数量
visitedGrid.clear(); // 每次使用时，清空
if (grid[i][j] == 0) {
for (int k = 0; k < 4; k++) {
int neari = i + dir[k][1]; // 计算相邻坐标
int nearj = j + dir[k][0];
if (neari < 0 || neari >= n || nearj < 0 || nearj >= m) continue;
if (visitedGrid.count(grid[neari][nearj])) continue; // 添加过的岛屿不要重复添加
// 把相邻四面的岛屿数量加起来
count += gridNum[grid[neari][nearj]];
visitedGrid.insert(grid[neari][nearj]); // 标记该岛屿已经添加过
}
}
result = max(result, count);
}
}
cout << result << endl;
}
岛屿的周长
给定一个由 1（陆地）和 0（水）组成的矩阵，岛屿是被水包围，并且通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设矩阵外均被水包围。在矩阵中恰好拥有一个岛屿，假设组成岛屿的陆地边长都为 1，请计算岛屿的周长。岛屿内部没有水域。
对于一个陆地格子的每条边，它被算作岛屿的周长当且仅当这条边为网格的边界或者相邻的另一个格子为水域。 因此，我们可以遍历每个陆地格子，看其四个方向是否为边界或者水域，如果是，将这条边的贡献（即 1）加入答案 ans 中即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
vector<vector<int>> dirs{{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
int islandPerimeter(vector<vector<int>>& grid) {
// 1.遍历网格 如果遇到陆地 计算周围的空格或者边界数
int m = grid.size();
int n = grid[0].size();
int counts{};
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 0) {
continue;
}
// 陆地
for (auto dir : dirs) {
int nx = dir[0] + i;
int ny = dir[1] + j;
if (nx < 0 || nx >= m || ny < 0 || ny >= n || grid[nx][ny] == 0) {
counts++;
}
}
}
}
return counts;
}
};
字符串接龙
字典 strList 中从字符串 beginStr 和 endStr 的转换序列是一个按下述规格形成的序列：
- 序列中第一个字符串是 beginStr。
- 序列中最后一个字符串是 endStr。
- 每次转换只能改变一个位置的字符（例如 ftr 可以转化 fty ，但 ftr 不能转化 frx）。
- 转换过程中的中间字符串必须是字典 strList 中的字符串。
- beginStr 和 endStr 不在 字典 strList 中
- 字符串中只有小写的26个字母
给你两个字符串 beginStr 和 endStr 和一个字典 strList，找到从 beginStr 到 endStr 的最短转换序列中的字符串数目。如果不存在这样的转换序列，返回 0。
这道题要解决两个问题：
1、图中的线是如何连在一起的
在搜索的过程中，我们可以枚举，用26个字母替换当前字符串的每一个字符，在看替换后是否在 strList里出现过，就可以判断 两个字符串 是否是链接的。
2、起点和终点的最短路径长度
首先题目中并没有给出点与点之间的连线，而是要我们自己去连，条件是字符只能差一个。
所以判断点与点之间的关系，需要判断是不是差一个字符，如果差一个字符，那就是有链接。
然后就是求起点和终点的最短路径长度，在无权图中，求最短路，用深搜或者广搜就行，没必要用最短路算法。
求起点和终点的最短路径长度，在无权图中，求最短路，用深搜或者广搜就行，没必要用最短路算法。
在无权图中，用广搜求最短路最为合适，广搜只要搜到了终点，那么一定是最短的路径。因为广搜就是以起点中心向四周扩散的搜索1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
using namespace std;
int main() {
int n;
cin>>n;
string beginStr,endStr;
cin>>beginStr>>endStr;
unordered_set<string> uset;
while(n--) {
string tmp;
cin>>tmp;
uset.insert(tmp);
}
// 使用广搜
queue<string> path;
path.push(beginStr);
unordered_map<string,int> visitMap;
visitMap.insert({beginStr,1});
while(!path.empty()) {
auto s = path.front();
path.pop();
int pathLen = visitMap[s];
// 替换字符串中字符
for(int i = 0;i<s.size();i++) {
string newWord = s;
for(int j = 0;j<26;j++) {
newWord[i] = j+'a';
if(newWord == endStr) {
cout<<pathLen+1<<'\n';
return 0;
}
if(uset.count(newWord)&& !visitMap.count(newWord)) {
// 包含该字符串
// 加入路径
visitMap.insert({newWord,pathLen+1});
path.push(newWord);
}
}
}
}
cout<< 0<<'\n';
return 0;
}
有向图的完全联通
给定一个有向图，包含 N 个节点，节点编号分别为 1，2，…，N。现从 1 号节点开始，如果可以从 1 号节点的边可以到达任何节点，则输出 1，否则输出 -1。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
using namespace std;
void dfs(vector<vector<int>>& graph,vector<bool>& visited,int target,int& counts) {
for(int t:graph[target]) {
if(visited[t]) {
continue;
}
visited[t] = true;
counts++;
dfs(graph,visited,t,counts);
}
}
int main() {
int n,k;
cin>>n>>k;
// unordered_map<int,int> umap;
vector<vector<int>> graph(n+1);
while(k--) {
int i,j;
cin>>i>>j;
graph[i].push_back(j);
}
vector<bool> visited(n+1);
visited[1] = true;
int counts {1};
dfs(graph,visited,1,counts);
if(counts == n) {
cout<<1;
}else{
cout<<-1;
}
return 0;
}
寻找存在的路径
给定一个包含 n 个节点的无向图中，节点编号从 1 到 n （含 1 和 n ）。你的任务是判断是否有一条从节点 source 出发到节点 destination 的路径存在。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
using namespace std;
bool dfs(vector<vector<int>>& graph,int next,vector<bool>& visited,int target) {
for(int t:graph[next]) {
if(visited[t]) {
continue;
}
if(t == target) {
return true;
}
visited[t] = true;
if(dfs(graph,t,visited,target)) {
return true;
}
}
return false;
}
int main() {
int n,m;
cin>>n>>m;
vector<vector<int>> graph(n+1); //邻接表实现
// vector<vector<int>> graph(n+1,vector<int>(n+1)) // 邻接矩阵实现
while(m--) {
int s,t;
cin>>s>>t;
graph[s].push_back(t);
graph[t].push_back(s);
}
int s,t;
cin>>s>>t;
vector<bool> visited(n+1);
visited[s] = true;
if(dfs(graph,s,visited,t)) {
cout<<1;
return 0;
}
cout<<0;
return 0;
}
也可以使用并查集,本题是并查集基础题目。 并查集主要解决就是集合问题，两个节点在不在一个集合，也可以将两个节点添加到一个集合中1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
using namespace std;
static vector<int> parent(101);
// 实现并查集 路径压缩
int find(int n) {
if(n == parent[n]) {
return n;
}
return parent[n] = find(parent[n]);
}
bool isSame(int i,int j) {
i = find(i);
j = find(j);
return i==j;
}
void join(int i,int j){
i = find(i);
j = find(j);
if(i ==j) {
return;
}
parent[i] = j;
}
int main() {
int n,m;
cin>>n>>m;
// 1.初始化并查集
for(int i =1;i<=n;++i) {
parent[i] = i;
}
while(m--) {
int s,t;
cin>>s>>t;
// 2.合并集合
join(s,t);
}
int s,t;
cin>>s>>t;
// 3. 查询两个节点是否是同一集合
if(isSame(s,t)) {
cout<<1;
}else{
cout<<0;
}
return 0;
}
冗余连接
树可以看成是一个连通且 无环 的 无向 图。
给定一个图，该图从一棵 n 个节点 (节点值 1～n) 的树中添加一条边后获得。添加的边的两个不同顶点编号在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。
请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的那个1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38class Solution {
public:
// 并查集
int find(int n, vector<int>& parent) {
return n == parent[n] ? n : parent[n] = find(parent[n],parent);
}
void join(int i, int j, vector<int>& parent) {
i = find(i, parent);
j = find(j, parent);
if (i == j) {
return;
}
parent[i] = j;
}
bool isSame(int i, int j, vector<int>& parent) {
i = find(i, parent);
j = find(j, parent);
return i == j;
}
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
// 1.初始化并查集
vector<int> parent(n + 1);
for (int i = 1; i <= n; ++i) {
parent[i] = i;
}
// 2.添加到集合
for (auto edge : edges) {
if (isSame(edge[0], edge[1], parent)) {
// 来自同一集合
return edge;
} else {
join(edge[0], edge[1], parent);
}
}
return {};
}
};
冗余连接II
在本问题中，有根树指满足以下条件的 有向 图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。
输入一个有向图，该图由一个有着 n 个节点（节点值不重复，从 1 到 n）的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间，这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi]，用以表示 有向 图中连接顶点 ui 和顶点 vi 的边，其中 ui 是 vi 的一个父节点。
返回一条能删除的边，使得剩下的图是有 n 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。
本题的本质是 ：有一个有向图，是由一颗有向树 + 一条有向边组成的 （所以此时这个图就不能称之为有向树），现在让我们找到那条边 把这条边删了，让这个图恢复为有向树。
还有“若有多条边可以删除，请输出标准输入中最后出现的一条边”，这说明在两条边都可以删除的情况下，要删顺序靠后的边！
如果是有向树的话，只有根节点入度为0，其他节点入度都为1（因为该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点）。如果发现入度为2的节点，需要判断 删除哪一条边，删除后本图能成为有向树。如果是删哪个都可以，优先删顺序靠后的边。果没有入度为2的点，说明 图中有环了1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81class Solution {
public:
vector<int> parent;
void init(int n) {
parent.resize(n + 1);
for (int i = 1; i <= n; i++) {
parent[i] = i;
}
}
int find(int n) { return n == parent[n] ? n : parent[n] = find(parent[n]); }
bool isSame(int i, int j) {
i = find(i);
j = find(j);
return i == j;
}
void join(int i, int j) {
i = find(i);
j = find(j);
if (i == j) {
return;
}
parent[i] = j;
}
bool isTreeAfterRemoveEdge(vector<vector<int>>& edges, int idx) {
// 删除这条边之后的图 是否是有向树
// 也就是检查是否包含有向环
for (int i = 0; i < edges.size(); ++i) {
if (i == idx) {
continue;
}
int x = edges[i][0];
int y = edges[i][1];
if (isSame(x, y)) {
// 同一集合
return false;
} else {
join(x, y);
}
}
return true;
}
vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
int n = edges.size();
// 先找到入度为2的节点 这个节点的两条边其中一条一定删除
// 检测删除之后是否为环
// 记录入度
// 检测包含入度为2的节点的边
vector<int> vec;
vector<int> inDegrees(n + 1);
for (int i = 0; i < edges.size(); ++i) {
auto edge = edges[i];
inDegrees[edge[1]]++;
}
for (int i = edges.size()-1;i>=0;--i) {
if (inDegrees[edges[i][1]] >= 2) {
vec.push_back(i);
}
}
init(n);
if (vec.size() > 0) {
if (isTreeAfterRemoveEdge(edges, vec[0])) {
return edges[vec[0]]; // 如果删除这个边后不是树 表明形成了有向环
// 利用无向图的方法判断
} else {
return edges[vec[1]];
}
}
// 没有入度为2 删除形成有向环的最后一条边
for (auto edge : edges) {
int x = edge[0];
int y = edge[1];
if (isSame(x, y)) {
return edge;
} else {
join(x, y);
}
}
return {};
}
};
有向图和无向图的环检测
对于无向图,可以使用并查集或者DFS深搜检测环
深搜的时候需要使用visited数组检测是否访问并且是否是父节点. 如果访问过了且不是父节点则说明有环.在DFS遍历过程中，每个节点都有以下三种状态：
- 未访问（UNVISITED）：节点尚未被DFS访问过。
- 正在访问（VISITING）：节点已经被DFS访问，但其所有邻居都还没有被遍历完毕。换句话说，它在当前的递归调用栈中。
- 已访问（VISITED）：节点及其所有邻居都已被完全遍历。
算法步骤
- 数据结构：
- 使用邻接表来表示有向图。
- 创建一个数组或哈希表来存储每个节点的状态，初始都为
UNVISITED。
- 主循环：
- 遍历图中的每个节点。
- 如果一个节点是
UNVISITED状态，就从它开始调用DFS，以防图是不连通的。 - 如果DFS函数返回
true（表示找到环），则整个算法可以立即停止并返回true。
- DFS 函数：
- DFS函数接受当前节点
u作为参数。 - 将
u的状态设置为VISITING。 - 遍历
u的所有邻居v：- 如果
v的状态是VISITING，说明v正在当前的DFS路径上，并且有一条边u -> v，这就形成了一个环。立即返回true。 - 如果
v的状态是UNVISITED，则对v进行递归DFS。如果dfs(v)返回true，也说明在子路径上找到了环，直接返回true。
- 如果
- 如果
u的所有邻居都已处理完毕，说明从u开始的路径上没有环。将u的状态设置为VISITED，并返回false
- DFS函数接受当前节点
1 |
|
有向图检测有向环可以通过拓扑排序或者dfs深搜
一个有向无环图（DAG）才能进行拓扑排序。如果一个有向图存在环，则无法进行完整的拓扑排序。
计算所有节点的入度（in-degree）。将所有入度为 0 的节点放入一个队列中。
循环直到队列为空：
- 从队列中取出一个节点
u。 - 将
u计入排序结果。 - 对于
u的每一个邻居v：- 将
v的入度减一。 - 如果
v的入度变为 0，则将其放入队列。
- 将
如果排序结果中的节点数量小于图的总节点数，则说明图中存在环。这是因为环中的节点入度永远不会变为 0，所以它们永远不会进入队列。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
class Graph {
private:
int V; // 节点数
std::vector<std::list<int>> adj; // 邻接表
std::vector<int> state; // 0: UNVISITED, 1: VISITING, 2: VISITED
// DFS 递归函数
bool isCyclicUtil(int u) {
state[u] = 1; // 设置为 VISITING
// 遍历当前节点 u 的所有邻居
for (int v : adj[u]) {
if (state[v] == 1) { // 如果邻居 v 正在被访问，则存在环
return true;
}
if (state[v] == 0) { // 如果邻居 v 未被访问，继续 DFS
if (isCyclicUtil(v)) {
return true;
}
}
}
state[u] = 2; // 所有子树都已访问完毕，设置为 VISITED
return false;
}
public:
Graph(int V) : V(V), adj(V), state(V, 0) {}
// 添加有向边
void addEdge(int u, int v) {
adj[u].push_back(v);
}
// 主函数，用于检测环
bool isCyclic() {
for (int i = 0; i < V; ++i) {
if (state[i] == 0) {
if (isCyclicUtil(i)) {
return true;
}
}
}
return false;
}
};
int main() {
// 示例 1: 有环图
Graph g1(4);
g1.addEdge(0, 1);
g1.addEdge(0, 2);
g1.addEdge(1, 2);
g1.addEdge(2, 0); // 环: 2 -> 0 -> 2
g1.addEdge(2, 3);
g1.addEdge(3, 3); // 自环
if (g1.isCyclic()) {
std::cout << "图1包含环" << std::endl;
} else {
std::cout << "图1不包含环" << std::endl;
}
// 示例 2: 无环图
Graph g2(4);
g2.addEdge(0, 1);
g2.addEdge(0, 2);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
if (g2.isCyclic()) {
std::cout << "图2包含环" << std::endl;
} else {
std::cout << "图2不包含环" << std::endl;
}
return 0;
}
图算法
- 最短路径算法（Shortest Path Algorithms）
这类算法用于在图中找到从一个节点到另一个节点或所有节点的最短路径。
- Dijkstra（迪杰斯特拉）算法
- 目的：计算从单个源点到图中所有其他节点的最短路径。
- 特点：适用于边权值为非负数的图。它的核心思想是贪心，每次选择离源点最近的未访问节点进行扩展。
- 应用：GPS 导航中的最短路径规划、网络路由协议（如 OSPF）。
- Floyd-Warshall（弗洛伊德-沃舍尔）算法
- 目的：计算图中所有节点对之间的最短路径。
- 特点：适用于边权值为正或负的图（但不能有负权环）。它通过动态规划思想，逐步考虑所有中间节点来优化路径。
- 应用：计算交通网络中任意两点之间的最短距离。
- Bellman-Ford（贝尔曼-福特）算法
- 目的：与 Dijkstra 类似，也是计算单个源点到所有节点的最短路径。
- 特点：可以处理边权值为负数的情况，但不能处理负权环。如果图中存在负权环，它能检测出来。
- 应用：路由协议 RIP。
- 最小生成树算法（Minimum Spanning Tree, MST）
这类算法用于找到一个连接图中所有节点，且总边权值最小的子图，这个子图就是所谓的最小生成树。
- Kruskal（克鲁斯卡尔）算法
- 目的：构建图的最小生成树。
- 特点：它是一种贪心算法。核心思想是按边权值从小到大排序，依次添加边，但要避免形成环。通常使用并查集（Union-Find）来高效地检测环。
- 应用：网络布线、集群分析。
- Prim（普里姆）算法
- 目的：同样是构建图的最小生成树。
- 特点：也是贪心算法。它从一个起始节点开始，每次选择连接已选节点和未选节点的边中，权值最小的那条边。
- 应用：与 Kruskal 类似，用于设计最优网络拓扑。
- 遍历算法（Traversal Algorithms）
这类算法用于系统地访问图中的所有节点。
- BFS (Breadth-First Search, 广度优先搜索)
- 目的：按层次遍历图中的所有节点。
- 特点：从一个起始节点开始，先访问其所有邻居，然后访问邻居的邻居，以此类推。通常使用队列（Queue）来实现。
- 应用：社交网络中的好友关系搜索、求解无权图中的最短路径。
- DFS (Depth-First Search, 深度优先搜索)
- 目的：沿着一条路径尽可能深地遍历图。
- 特点：从一个起始节点开始，沿着一条路径一直走到底，直到无路可走，然后回溯到上一个节点，继续沿着另一条路径走。通常使用栈（Stack）或递归来实现。
- 应用：拓扑排序、寻找图的连通分量、检测环。
- 其他重要图算法
- 拓扑排序（Topological Sort）：用于对有向无环图（DAG）中的节点进行线性排序。如果图中有环，则无法进行拓扑排序。
- 最大流/最小割：这类算法解决网络流问题，比如在给定网络中，从源点到汇点的最大流量。
- PageRank：一种用于网页排序的算法，通过计算网页链接的重要性来确定其排名
最短路径
Dijkstra
解决问题：单源最短路径。也就是从图中一个固定的起点出发，到所有其他可达顶点的最短路径。
核心思想：这是一种贪心算法。它维护一个集合，存放已确定最短路径的顶点。算法从起点开始，每次都从剩余的顶点中，选择那个离起点最近（最短路径已估算）的顶点，将其加入集合，并用它来更新其所有邻居到起点的距离。
Dijkstra 算法用于在一个带权图中找到从一个起始节点到所有其他节点的最短路径。
Dijkstra 算法维护一个节点集合，这个集合中的节点已经确定了最短路径。它从起始节点开始，不断选择距离起始节点最近的未访问节点，并用这个节点来更新其所有邻接节点的距离。这个过程重复进行，直到所有节点都被访问。
算法步骤
- 初始化：创建一个距离数组
dist，将起始节点的距离设为 0，其他所有节点的距离设为无穷大。 - 优先队列：使用一个最小优先队列来存储
<距离, 节点>对，初始时将<0, 起始节点>放入队列。 - 循环：只要优先队列不为空，就执行以下操作：
- 从队列中弹出距离最小的节点
u。 - 如果
u已经被访问过，则跳过。 - 标记
u为已访问。 - 遍历
u的所有邻接节点v：- 计算通过
u到v的新距离：new_dist = dist[u] + weight(u, v)。 - 如果
new_dist < dist[v]，则更新dist[v] = new_dist，并将<new_dist, v>放入优先队列。
- 计算通过
- 从队列中弹出距离最小的节点
- 结果：当循环结束时，
dist数组中存储的就是起始节点到所有其他节点的最短距离。
适用场景
- 寻找最短路径，例如，导航系统计算两个地点之间的最短距离。
- 要求所有边权都为非负数。如果图中存在负权边，Dijkstra 算法会失效，此时需要使用 Bellman-Ford 或 SPFA 算法。
dijkstra算法：在有权图（权值非负数）中求从起点到其他节点的最短路径算法。
需要注意两点：
- dijkstra 算法可以同时求起点到所有节点的最短路径
- 权值不能为负数
dijkstra 算法同样是贪心的思路，不断寻找距离源点最近的没有访问过的节点。
这里也给出 dijkstra三部曲：
- 第一步，选源点到哪个节点近且该节点未被访问过
- 第二步，该最近节点被标记访问过
- 第三步，更新非访问节点到源点的距离（即更新minDist数组
参加科学大会
小明是一位科学家，他需要参加一场重要的国际科学大会，以展示自己的最新研究成果。
小明的起点是第一个车站，终点是最后一个车站。然而，途中的各个车站之间的道路状况、交通拥堵程度以及可能的自然因素（如天气变化）等不同，这些因素都会影响每条路径的通行时间。
小明希望能选择一条花费时间最少的路线，以确保他能够尽快到达目的地。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
using namespace std;
class mycomp {
public:
bool operator()(const pair<int,int>& a,const pair<int,int>& b) {
return a.second>b.second;
}
};
typedef struct Edge{
int to;
int val;
Edge(int _to,int _val):to(_to),val(_val){}
}Edge;
int main() {
int n,m;
cin>>n>>m;
// 使用邻接表和最小堆优化
vector<int> minDist(n+1,numeric_limits<int>::max()); // 最短距离 // 存储从源点到每个节点的最短距离
// <节点,到源点最短距离>
priority_queue<pair<int,int>,vector<pair<int,int>>,mycomp>pq;// 定义小堆
vector<bool> visited(n+1); //标记是否访问
vector<list<Edge>> grid(n+1); // 邻接表
minDist[1] = 0;
pq.push({1,0}); // 加入节点和距离源节点最短距离
while(m--) {
int s,t,val;
cin>>s>>t>>val;
grid[s].push_back({t,val});
}
while(!pq.empty()) {
auto cur = pq.top(); // 找到距离源点最近点
pq.pop();
if(visited[cur.first]) {
continue;
}
visited[cur.first] = true;
// 从该点出发更新最短距离
for(Edge edge:grid[cur.first]) {
// 遍历能到达的边 如果距离+minDist[cur.first] 比minDist[edge.to]小 更新
if(!visited[edge.to] && minDist[edge.to]>minDist[cur.first]+edge.val) {
minDist[edge.to] = minDist[cur.first]+edge.val;
pq.push({edge.to,minDist[edge.to]}); // 加入源点能到达的边
}
}
}
if(minDist[n] == numeric_limits<int>::max()) {
cout<<-1;
}else{
cout<<minDist[n];
}
return 0;
// dijkstra 从节点开始选择 使用邻接矩阵
vector<vector<int>> grid(n+1,vector<int>(n+1,numeric_limits<int>::max()));
vector<bool> visited(n+1);
while(m--) {
int s,t,val;
cin>>s>>t>>val;
grid[s][t] = val;
}
vector<int> minDist(n+1,numeric_limits<int>::max()); // 到达源节点时间
minDist[1] = 0;
for(int i = 1;i<=n;++i) { // 找到n-1个点 距离源节点时间最小
int dist{numeric_limits<int>::max()};
int cur = 1;
for(int j = 1;j<=n;++j) {
if(!visited[j] && minDist[j]<dist) {
dist = minDist[j];
cur = j;
}
}
// 更新 已访问 距离源节点距离确定
visited[cur] = true;
// 更新其他节点到源节点距离
for(int j = 1;j<=n;j++) {
if(!visited[j] && grid[cur][j] != numeric_limits<int>::max() && minDist[j] >minDist[cur]+grid[cur][j]) {
minDist[j] = minDist[cur] + grid[cur][j];
}
}
}
if(minDist[n] == numeric_limits<int>::max()) {
cout<<-1<<'\n';
}else{
cout<<minDist[n]<<'\n';
}
return 0;
}
prim是求 非访问节点到最小生成树的最小距离，而 dijkstra是求 非访问节点到源点的最小距离。
prim 更新 minDist数组的写法：1
2
3
4
5for (int j = 1; j <= v; j++) {
if (!isInTree[j] && grid[cur][j] < minDist[j]) {
minDist[j] = grid[cur][j];
}
}
因为 minDist表示 节点到最小生成树的最小距离，所以 新节点cur的加入，只需要 使用 grid[cur][j] ，grid[cur][j] 就表示 cur 加入生成树后，生成树到 节点j 的距离。
dijkstra 更新 minDist数组的写法：1
2
3
4
5for (int v = 1; v <= n; v++) {
if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
minDist[v] = minDist[cur] + grid[cur][v];
}
}
因为 minDist表示 节点到源点的最小距离，所以 新节点 cur 的加入，需要使用 源点到cur的距离 （minDist[cur]） + cur 到 节点 v 的距离 （grid[cur][v]），才是 源点到节点v的距离。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
using namespace std;
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<vector<int>> grid(n + 1, vector<int>(n + 1, INT_MAX));
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
grid[p1][p2] = val;
}
int start = 1;
int end = n;
//加上初始化
vector<int> parent(n + 1, -1);
// 存储从源点到每个节点的最短距离
std::vector<int> minDist(n + 1, INT_MAX);
// 记录顶点是否被访问过
std::vector<bool> visited(n + 1, false);
minDist[start] = 0; // 起始点到自身的距离为0
for (int i = 1; i <= n; i++) { // 遍历所有节点
int minVal = INT_MAX;
int cur = 1;
// 1、选距离源点最近且未访问过的节点
for (int v = 1; v <= n; ++v) {
if (!visited[v] && minDist[v] < minVal) {
minVal = minDist[v];
cur = v;
}
}
visited[cur] = true; // 2、标记该节点已被访问
// 3、第三步，更新非访问节点到源点的距离（即更新minDist数组）
for (int v = 1; v <= n; v++) {
if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
minDist[v] = minDist[cur] + grid[cur][v];
parent[v] = cur;// 记录边
}
}
}
// 输出最短情况
for (int i = 1; i <= n; i++) {
cout << parent[i] << "->" << i << endl;
}
if (minDist[end] == INT_MAX) cout << -1 << endl; // 不能到达终点
else cout << minDist[end] << endl; // 到达终点最短路径
}
对于求解带有负权值的最短路问题，可以使用 Bellman-Ford 算法
dijkstra的堆优化
使用邻接表实现1
2
3
4
5
6
7struct Edge {
int to; // 链接的节点
int val; // 边的权重
Edge(int t, int w): to(t), val(w) {} // 构造函数
};
vector<list<Edge>> grid(n + 1); // 邻接表1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
for (int i = 1; i <= n; i++) { // 遍历所有节点，第一层for循环
int minVal = INT_MAX;
int cur = 1;
// 1、选距离源点最近且未访问过的节点 ， 第二层for循环
for (int v = 1; v <= n; ++v) {
if (!visited[v] && minDist[v] < minVal) {
minVal = minDist[v];
cur = v;
}
}
visited[cur] = true; // 2、标记该节点已被访问
// 3、第三步，更新非访问节点到源点的距离（即更新minDist数组）
for (int v = 1; v <= n; v++) {
if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
minDist[v] = minDist[cur] + grid[cur][v];
}
}
}
思路依然是 dijkstra 三部曲：
- 第一步，选源点到哪个节点近且该节点未被访问过
- 第二步，该最近节点被标记访问过
- 第三步，更新非访问节点到源点的距离（即更新minDist数组）
只不过之前是 通过遍历节点来遍历边，通过两层for循环来寻找距离源点最近节点。 这次我们直接遍历边，且通过堆来对边进行排序，达到直接选择距离源点最近节点。
要选择距离源点近的节点（即：该边的权值最小），所以需要一个 小顶堆来对边的权值排序，每次从小顶堆堆顶 取边就是权值最小的边。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
using namespace std;
// 小顶堆
class mycomparison {
public:
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
return lhs.second > rhs.second;
}
};
// 定义一个结构体来表示带权重的边
struct Edge {
int to; // 邻接顶点
int val; // 边的权重
Edge(int t, int w): to(t), val(w) {} // 构造函数
};
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<list<Edge>> grid(n + 1);
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2，权值为 val
grid[p1].push_back(Edge(p2, val));
}
int start = 1; // 起点
int end = n; // 终点
// 存储从源点到每个节点的最短距离
std::vector<int> minDist(n + 1, INT_MAX);
// 记录顶点是否被访问过
std::vector<bool> visited(n + 1, false);
// 优先队列中存放 pair<节点，源点到该节点的权值>
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pq;
// 初始化队列，源点到源点的距离为0，所以初始为0
pq.push(pair<int, int>(start, 0));
minDist[start] = 0; // 起始点到自身的距离为0
while (!pq.empty()) {
// 1. 第一步，选源点到哪个节点近且该节点未被访问过 （通过优先级队列来实现）
// <节点， 源点到该节点的距离>
pair<int, int> cur = pq.top(); pq.pop();
if (visited[cur.first]) continue;
// 2. 第二步，该最近节点被标记访问过
visited[cur.first] = true;
// 3. 第三步，更新非访问节点到源点的距离（即更新minDist数组）
for (Edge edge : grid[cur.first]) { // 遍历 cur指向的节点，cur指向的节点为 edge
// cur指向的节点edge.to，这条边的权值为 edge.val
if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDist
minDist[edge.to] = minDist[cur.first] + edge.val;
pq.push(pair<int, int>(edge.to, minDist[edge.to]));
}
}
}
if (minDist[end] == INT_MAX) cout << -1 << endl; // 不能到达终点
else cout << minDist[end] << endl; // 到达终点最短路径
}
Bellman-ford算法
Bellman_ford算法的核心思想是 对所有边进行松弛n-1次操作（n为节点数量），从而求得目标最短路。
要求最小权值，那么 这两个状态我们就取最小的1
if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value
也就是说，如果 通过 A 到 B 这条边可以获得更短的到达B节点的路径，即如果 minDist[B] > minDist[A] + value，那么我们就更新 minDist[B] = minDist[A] + value ，这个过程就叫做 “松弛” 。
以上讲了这么多，其实都是围绕以下这句代码展开：1
if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value
这句代码就是 Bellman_ford算法的核心操作。以上代码也可以这么写：minDist[B] = min(minDist[A] + value, minDist[B])
对所有边松弛一次，相当于计算 起点到达 与起点一条边相连的节点 的最短距离。
与起点（节点1）一条边相邻的节点，到达节点2 最短距离是 1，到达节点3 最短距离是5。
而 节点1 -> 节点2 -> 节点5 -> 节点3 这条路线 是 与起点 三条边相连的路线了。
所以对所有边松弛一次 能得到 与起点 一条边相连的节点最短距离。
那对所有边松弛两次 可以得到与起点 两条边相连的节点的最短距离。
那对所有边松弛三次 可以得到与起点 三条边相连的节点的最短距离，这个时候，我们就能得到到达节点3真正的最短距离，也就是 节点1 -> 节点2 -> 节点5 -> 节点3 这条路线。
节点数量为n，那么起点到终点，最多是 n-1 条边相连。那么无论图是什么样的，边是什么样的顺序，对所有边松弛 n-1 次 就一定能得到 起点到达 终点的最短距离。其实也同时计算出了，起点 到达 所有节点的最短距离，因为所有节点与起点连接的边数最多也就是 n-1 条边。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
using namespace std;
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<vector<int>> grid;
// 将所有边保存起来
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2，权值为 val
grid.push_back({p1, p2, val});
}
int start = 1; // 起点
int end = n; // 终点
vector<int> minDist(n + 1 , INT_MAX);
minDist[start] = 0;
for (int i = 1; i < n; i++) { // 对所有边 松弛 n-1 次
for (vector<int> &side : grid) { // 每一次松弛，都是对所有边进行松弛
int from = side[0]; // 边的出发点
int to = side[1]; // 边的到达点
int price = side[2]; // 边的权值
// 松弛操作
// minDist[from] != INT_MAX 防止从未计算过的节点出发
if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) {
minDist[to] = minDist[from] + price;
}
}
}
if (minDist[end] == INT_MAX) cout << "unconnected" << endl; // 不能到达终点
else cout << minDist[end] << endl; // 到达终点最短路径
}
城市间的货物运输
某国为促进城市间经济交流，决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市，通过道路网络连接，网络中的道路仅允许从某个城市单向通行到另一个城市，不能反向通行。
网络中的道路都有各自的运输成本和政府补贴，道路的权值计算方式为：运输成本 - 政府补贴。
权值为正表示扣除了政府补贴后运输货物仍需支付的费用；权值为负则表示政府的补贴超过了支出的运输成本，实际表现为运输过程中还能赚取一定的收益。
请找出从城市 1 到城市 n 的所有可能路径中，综合政府补贴后的最低运输成本。
如果最低运输成本是一个负数，它表示在遵循最优路径的情况下，运输过程中反而能够实现盈利。
城市 1 到城市 n 之间可能会出现没有路径的情况，同时保证道路网络中不存在任何负权回路。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
using namespace std;
typedef struct Edge{
int to;
int val;
}Edge;
int main() {
int n,m;
cin>>n>>m;
// vector<list<Edge>> grid(n+1);
vector<vector<int>> grid;
while(m--) {
int s,t,val;
cin>>s>>t>>val;
// grid[s].push_back({t,val}); // 邻接表实现
grid.push_back({s,t,val}); // 存取边以及值
}
vector<int> minDist(n+1,numeric_limits<int>::max());
minDist[1] = 0;
// 对所有边松弛n-1次
// 遍历所有边
for(int i = 1;i<n;++i) {
for(vector<int>& side : grid) {
// 如果i可达 并且i到达p.to+p.val的距离小于minDist[p.to] 更新
int s=side[0];
int t=side[1];
int val=side[2];
if(minDist[s]!=numeric_limits<int>::max() && minDist[s]+val<minDist[t]) {
minDist[t] = minDist[s] + val;
}
}
}
if(minDist[n] == numeric_limits<int>::max()) {
cout<<"unconnected";
}else{
cout<<minDist[n];
}
return 0;
}
Bellman_ford 是可以计算负权值的单源最短路算法。其算法核心思路是对所有边进行 n-1 次 松弛。
SPFA 算法的核心思想
SPFA与Bellman-Ford是同一种算法. 但SPFA是BF的队列优化版本.
在SPFA 算法中，我们通过对所有边进行 V−1 次“松弛”操作来找到最短路径。这个过程是盲目的，即使在某次循环中没有边的路径被更新，它也会继续执行。
SPFA 算法的改进之处在于，它利用一个队列来存储那些可能导致其邻接点路径变短的顶点。它遵循以下原则：
- 只有当一个顶点的最短路径被更新时，它才可能引起其邻居的最短路径发生变化。
- 因此，我们只将被松弛的顶点放入一个队列中。
这种“懒惰”的策略避免了对所有边进行重复的、不必要的检查，从而在大多数情况下显著提高了效率。
SPFA 的工作流程
- 初始化：
- 创建一个距离数组
dist，将源点s的距离设为 0，其他所有顶点的距离设为无穷大。 - 创建一个队列
Q，并将源点s入队。 - 创建一个布尔数组
in_queue，用于标记顶点是否在队列中。
- 创建一个距离数组
- 循环：
- 只要队列
Q不为空，就重复以下步骤：- 从
Q中取出一个顶点u，并将其in_queue标记设为 false。 - 遍历
u的所有邻接点v，执行松弛操作：如果dist[u] + weight(u, v) < dist[v]，则：- 更新
dist[v] = dist[u] + weight(u, v)。 - 如果
v当前不在队列中，将其入队，并设in_queue[v]为 true。
- 更新
- 从
- 只要队列
- 结果：
- 循环结束后，
dist数组中存储的就是从源点s到图中所有顶点的最短路径。 - 如果图中存在负权环，SPFA 算法将陷入无限循环。可以通过记录每个顶点入队的次数来检测负权环。如果一个顶点入队的次数超过了 V 次，说明存在负权环。
- 循环结束后，
只有当一个顶点的最短路径被更新后，才有可能导致它的邻居的路径被更新。因此，它使用一个队列来存储那些距离被更新、可能需要松弛其邻居的顶点。这种方式避免了对所有边的重复遍历，从而在平均情况下大大提高了效率
所以 Bellman_ford 算法 每次都是对所有边进行松弛，其实是多做了一些无用功。只需要对 上一次松弛的时候更新过的节点作为出发节点所连接的边进行松弛就够了1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
using namespace std;
struct Edge { //邻接表
int to; // 链接的节点
int val; // 边的权重
Edge(int t, int w): to(t), val(w) {} // 构造函数
};
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<list<Edge>> grid(n + 1);
vector<bool> isInQueue(n + 1); // 加入优化，已经在队里里的元素不用重复添加
// 将所有边保存起来
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2，权值为 val
grid[p1].push_back(Edge(p2, val));
}
int start = 1; // 起点
int end = n; // 终点
vector<int> minDist(n + 1 , INT_MAX);
minDist[start] = 0;
queue<int> que;
que.push(start);
while (!que.empty()) {
int node = que.front(); que.pop();
isInQueue[node] = false; // 从队列里取出的时候，要取消标记，我们只保证已经在队列里的元素不用重复加入
for (Edge edge : grid[node]) {
int from = node;
int to = edge.to;
int value = edge.val;
if (minDist[to] > minDist[from] + value) { // 开始松弛
minDist[to] = minDist[from] + value;
if (isInQueue[to] == false) { // 已经在队列里的元素不用重复添加
que.push(to);
isInQueue[to] = true;
}
}
}
}
if (minDist[end] == INT_MAX) cout << "unconnected" << endl; // 不能到达终点
else cout << minDist[end] << endl; // 到达终点最短路径
}
只需要对 上一次松弛的时候更新过的节点作为出发节点所连接的边 进行松弛就够了,有一个优化，用visited数组记录已经在队列里的元素，已经在队列的元素不用重复加入
SPFA（队列优化版Bellman_ford） 在理论上 时间复杂度更胜一筹，但实际上，也要看图的稠密程度，如果 图很大且非常稠密的情况下，虽然 SPFA的时间复杂度接近Bellman_ford，但实际时间消耗 可能是 SPFA耗时更多。
负权回路
在没有负权回路的图中，松弛 n 次以上 ，结果不会有变化。
但本题有 负权回路，如果松弛 n 次，结果就会有变化了，因为 有负权回路 就是可以无限最短路径（一直绕圈，就可以一直得到无限小的最短距离）。那么每松弛一次，都会更新最短路径，所以结果会一直有变化。
在 bellman_ford 算法中，松弛 n-1 次所有的边 就可以求得 起点到任何节点的最短路径，松弛 n 次以上，minDist数组（记录起到到其他节点的最短距离）中的结果也不会有改变 。有负权回路的情况下，一直都会有更短的最短路，所以 松弛 第n次，minDist数组 也会发生改变。
所以可以通过bellman_ford 算法,松弛第n次是看还是否有值改变.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
using namespace std;
int main() {
int n,m;
cin>>n>>m;
// 使用bellman-ford检测负权回路
// 在有负权回路下计算最小值
// 对所有边松弛n次
vector<vector<int>> grid;
while(m--) {
int s,t,val;
cin>>s>>t>>val;
grid.push_back({s,t,val});
}
bool flag{};
vector<int> minDist(n+1,numeric_limits<int>::max());
minDist[1] = 0;
for(int i=1;i<=n;++i) {
for(vector<int>& edge:grid) {
int s = edge[0];
int t = edge[1];
int val = edge[2];
if(minDist[s]!=numeric_limits<int>::max() && minDist[s]+val<minDist[t]) {
if(i != n) {
minDist[t] = minDist[s]+val;
}else{
// 还在变化
flag = true;
break;
}
}
}
if(flag) {
break;
}
}
if(flag) {
cout<<"circle";
return 0;
}
if(minDist[n] == numeric_limits<int>::max()) {
cout<<"unconnected";
}else{
cout<<minDist[n];
}
return 0;
}
上面的解法中对所有边松弛了n-1次后，再松弛一次，如果出现minDist出现变化就判断有负权回路。
使用队列优化版的bellman_ford（SPFA）
如果使用 SPFA 那么节点都是进队列的，那么节点进入队列几次后足够判断该图是否有负权回路呢？
在极端情况下，即：所有节点都与其他节点相连，每个节点的入度为 n-1 （n为节点数量），所以每个节点最多加入 n-1 次队列。那么如果节点加入队列的次数 超过了 n-1次 ，那么该图就一定有负权回路。
需要记录哪些节点已经出队列了，哪些节点在队列里面，对于已经出队列的节点不用统计入度，以下为优化后的代码：1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
using namespace std;
struct Edge { //邻接表
int to; // 链接的节点
int val; // 边的权重
Edge(int t, int w): to(t), val(w) {} // 构造函数
};
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<list<Edge>> grid(n + 1); // 邻接表
// 将所有边保存起来
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2，权值为 val
grid[p1].push_back(Edge(p2, val));
}
int start = 1; // 起点
int end = n; // 终点
vector<int> minDist(n + 1 , INT_MAX);
minDist[start] = 0;
queue<int> que;
que.push(start); // 队列里放入起点
vector<int> count(n+1, 0); // 记录节点加入队列几次
count[start]++;
vector<bool> inQueue(n+1, false); // 记录节点是否在队列中
bool flag = false;
while (!que.empty()) {
int node = que.front(); que.pop();
inQueue[node] = false; // 节点出队
for (Edge edge : grid[node]) {
int from = node;
int to = edge.to;
int value = edge.val;
if (minDist[to] > minDist[from] + value) { // 开始松弛
minDist[to] = minDist[from] + value;
if (!inQueue[to]) { // 避免重复入队
que.push(to);
inQueue[to] = true;
count[to]++;
if (count[to] == n) {// 如果加入队列次数超过 n-1次 就说明该图与负权回路
flag = true;
while (!que.empty()) que.pop();
break;
}
}
}
}
}
if (flag) cout << "circle" << endl;
else if (minDist[end] == INT_MAX) {
cout << "unconnected" << endl;
} else {
cout << minDist[end] << endl;
}
}
单源有限最短路径
某国为促进城市间经济交流，决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市，通过道路网络连接，网络中的道路仅允许从某个城市单向通行到另一个城市，不能反向通行。
网络中的道路都有各自的运输成本和政府补贴，道路的权值计算方式为：运输成本 - 政府补贴。
权值为正表示扣除了政府补贴后运输货物仍需支付的费用；
权值为负则表示政府的补贴超过了支出的运输成本，实际表现为运输过程中还能赚取一定的收益。
请计算在最多经过 k 个城市的条件下，从城市 src 到城市 dst 的最低运输成本。
使用Bellfman-ford算法,对所有边松弛一次,相当于计算起点到达与起点一条边相连的节点 的最短距离
节点数量为n，起点到终点，最多是 n-1 条边相连。 那么对所有边松弛 n-1 次 就一定能得到 起点到达 终点的最短距离。
本题计算minDist 一定要基于上次 的 minDist 数值。
其关键在于本题的两个因素：
- 本题可以有负权回路，说明只要多做松弛，结果是会变的。
- 本题要求最多经过k个节点，对松弛次数是有限制的
在对所有边松弛第一次的过程中，不仅仅与起点一条边相连的节点更新了，所有节点都更新了。而且对所有边的后面几次松弛，同样是更新了所有的节点，说明至多经过k 个节点这个限制 根本没有限制住，每个节点的数值都被更新了。计算minDist数组的时候，基于了本次松弛的 minDist数值，而不是上一次 松弛时候minDist的数值。
所以在每次计算 minDist 时候，要基于 对所有边上一次松弛的 minDist 数值才行，所以我们要记录上一次松弛的minDist。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
using namespace std;
int main() {
int n,m;
cin>>n>>m;
vector<vector<int>> grid;
while(m--) {
int s,t,val;
cin>>s>>t>>val;
grid.push_back({s,t,val});
}
int src,dst,k;
cin>>src>>dst>>k;
vector<int> minDist(n+1,numeric_limits<int>::max());
vector<int> copy_minDist(n+1);
minDist[src] = 0;
for(int i =1;i<=k+1;++i) {
copy_minDist = minDist;
for(auto& edge:grid) {
int x = edge[0];
int y = edge[1];
int val = edge[2];
// 注意使用 copy_minDist 来计算 minDist
if(copy_minDist[x]!=numeric_limits<int>::max() && copy_minDist[x]+val<minDist[y]) {
minDist[y] = copy_minDist[x]+val;
}
}
}
if(minDist[dst]!=numeric_limits<int>::max()) {
cout<<minDist[dst];
}else{
cout<<"unreachable";
}
return 0;
}
也可以使用SPFA,可以用一个变量 que_size 记录每一轮松弛入队列的所有节点数量。
下一轮松弛的时候，就把队列里 que_size 个节点都弹出来，就是上一轮松弛入队列的节点。
使用visited数组记录是否在队列,每一轮松弛中，重复节点可以不用入队列。
因为重复节点入队列，下次从队列里取节点的时候，该节点要取很多次，而且都是重复计算。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
using namespace std;
struct Edge { //邻接表
int to; // 链接的节点
int val; // 边的权重
Edge(int t, int w): to(t), val(w) {} // 构造函数
};
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<list<Edge>> grid(n + 1); // 邻接表
// 将所有边保存起来
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2，权值为 val
grid[p1].push_back(Edge(p2, val));
}
int start, end, k;
cin >> start >> end >> k;
k++;
vector<int> minDist(n + 1 , INT_MAX);
vector<int> minDist_copy(n + 1); // 用来记录每一次遍历的结果
minDist[start] = 0;
queue<int> que;
que.push(start); // 队列里放入起点
int que_size;
while (k-- && !que.empty()) {
vector<bool> visited(n + 1, false); // 每一轮松弛中，控制节点不用重复入队列
minDist_copy = minDist;
que_size = que.size();
while (que_size--) {
int node = que.front(); que.pop();
visited[node] = false;
for (Edge edge : grid[node]) {
int from = node;
int to = edge.to;
int price = edge.val;
if (minDist[to] > minDist_copy[from] + price) {
minDist[to] = minDist_copy[from] + price;
if(visited[to]) continue; // 不用重复放入队列，但需要重复松弛，所以放在这里位置
visited[to] = true;
que.push(to);
}
}
}
}
if (minDist[end] == INT_MAX) cout << "unreachable" << endl;
else cout << minDist[end] << endl;
}
Floyd-Warshall算法
- 解决问题：所有顶点对之间的最短路径。它可以一次性计算出图中任意两个顶点之间的最短路径。
- 核心思想：这是一种动态规划算法。它通过逐步增加中间节点的集合来找到最短路径。
- 工作流程：
- 初始化：创建一个距离矩阵，其中
dist[i][j]初始化为顶点i到j的边权值。 - 循环：使用三重嵌套循环：
- 最外层循环
k：表示中间顶点，从0到n-1。 - 内两层循环
i和j：表示起始和结束顶点。
- 最外层循环
- 在循环中，更新
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])。这个公式意味着，从i到j的最短路径，要么是已知的直接路径，要么是通过k作为中间点的新路径。
- 初始化：创建一个距离矩阵，其中
- 优点：能够处理负权边（但不能有负权环），实现简单。
- 缺点：时间复杂度为 O(n3)，比Dijkstra算法（使用优先队列时为 O(E+VlogV)）要慢，不适合用于稀疏图。
小明逛公园
小明喜欢去公园散步，公园内布置了许多的景点，相互之间通过小路连接，小明希望在观看景点的同时，能够节省体力，走最短的路径。
给定一个公园景点图，图中有 N 个景点（编号为 1 到 N），以及 M 条双向道路连接着这些景点。每条道路上行走的距离都是已知的。
小明有 Q 个观景计划，每个计划都有一个起点 start 和一个终点 end，表示他想从景点 start 前往景点 end。由于小明希望节省体力，他想知道每个观景计划中从起点到终点的最短路径长度。 请你帮助小明计算出每个观景计划的最短路径长度。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
using namespace std;
int main() {
int n,m;
cin>>n>>m;
// grid[i][j][k] 表示i到j经过k的最小值
vector<vector<vector<int>>> grid(n+1,vector<vector<int>>(n+1,vector<int>(n+1,10001)));
while(m--) {
int u,v,w;
cin>>u>>v>>w;
grid[u][v][0] = w;
grid[v][u][0] = w;
}
for(int k = 1;k<=n;k++) {
for(int u = 1;u<=n;u++) {
for(int v = 1;v<=n;v++) {
grid[u][v][k] =
min(grid[u][v][k-1],grid[u][k][k-1]+grid[k][v][k-1]);
}
}
}
int Q;
cin>>Q;
while(Q--) {
int s,t;
cin>>s>>t;
if(grid[s][t][n] == 10001) {
cout<<-1<<endl;
}else{
cout<<grid[s][t][n]<<endl;
}
}
return 0;
}
空间优化1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
using namespace std;
int main() {
int n,m;
cin>>n>>m;
// grid[i][j][k] 表示i到j经过k的最小值
// vector<vector<vector<int>>> grid(n+1,vector<vector<int>>(n+1,vector<int>(n+1,10001)));
vector<vector<int>> grid(n+1,vector<int>(n+1,10001));
while(m--) {
int u,v,w;
cin>>u>>v>>w;
grid[u][v] = w;
grid[v][u] = w;
}
for(int k = 1;k<=n;k++) {
for(int u = 1;u<=n;u++) {
for(int v = 1;v<=n;v++) {
grid[u][v] =
min(grid[u][k]+grid[k][v],grid[u][v]);
}
}
}
int Q;
cin>>Q;
while(Q--) {
int s,t;
cin>>s>>t;
if(grid[s][t] == 10001) {
cout<<-1<<endl;
}else{
cout<<grid[s][t]<<endl;
}
}
return 0;
}
如果遇到单源且边为正数，直接Dijkstra。
至于 使用朴素版还是 堆优化版 还是取决于图的稠密度， 多少节点多少边算是稠密图，多少算是稀疏图，这个没有量化，如果想量化只能写出两个版本然后做实验去测试，不同的判题机得出的结果还不太一样。
一般情况下，可以直接用堆优化版本。
如果遇到单源边可为负数，直接 Bellman-Ford，同样 SPFA 还是 Bellman-Ford 取决于图的稠密度。
一般情况下，直接用 SPFA。
如果有负权回路，优先 Bellman-Ford， 如果是有限节点最短路 也优先 Bellman-Ford，理由是写代码比较方便。
如果是遇到多源点求最短路，直接 Floyd。
A*算法
启发式算法,核心是使用启发式函数定义一个权重. 每个节点权重F=G+H. G：起点达到目前遍历节点的距离 H：目前遍历的节点到达终点的距离
起点达到目前遍历节点的距离 + 目前遍历的节点到达终点的距离 就是起点到达终点的距离。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
using namespace std;
int moves[1001][1001];
int dir[8][2]={-2,-1,-2,1,-1,2,1,2,2,1,2,-1,1,-2,-1,-2};
int b1, b2;
// F = G + H
// G = 从起点到该节点路径消耗
// H = 该节点到终点的预估消耗
struct Knight{
int x,y;
int g,h,f;
bool operator < (const Knight & k) const{ // 重载运算符， 从小到大排序
return k.f < f;
}
};
priority_queue<Knight> que;
int Heuristic(const Knight& k) { // 欧拉距离
return (k.x - b1) * (k.x - b1) + (k.y - b2) * (k.y - b2); // 统一不开根号，这样可以提高精度
}
void astar(const Knight& k)
{
Knight cur, next;
que.push(k);
while(!que.empty())
{
cur=que.top(); que.pop();
if(cur.x == b1 && cur.y == b2)
break;
for(int i = 0; i < 8; i++)
{
next.x = cur.x + dir[i][0];
next.y = cur.y + dir[i][1];
if(next.x < 1 || next.x > 1000 || next.y < 1 || next.y > 1000)
continue;
if(!moves[next.x][next.y])
{
moves[next.x][next.y] = moves[cur.x][cur.y] + 1;
// 开始计算F
next.g = cur.g + 5; // 统一不开根号，这样可以提高精度，马走日，1 * 1 + 2 * 2 = 5
next.h = Heuristic(next);
next.f = next.g + next.h;
que.push(next);
}
}
}
}
int main()
{
int n, a1, a2;
cin >> n;
while (n--) {
cin >> a1 >> a2 >> b1 >> b2;
memset(moves,0,sizeof(moves));
Knight start;
start.x = a1;
start.y = a2;
start.g = 0;
start.h = Heuristic(start);
start.f = start.g + start.h;
astar(start);
while(!que.empty()) que.pop(); // 队列清空
cout << moves[b1][b2] << endl;
}
return 0;
}
最小生成树的概念
最小生成树（Minimum Spanning Tree, MST）是图论中的一个核心概念，它指的是一个加权连通图的特殊子图
- 图：一个由节点（顶点）和边组成的集合。
- 加权图：图中的每条边都有一个权重（或成本、距离）。
- 连通图：图中任意两个节点之间都存在一条路径。
- 生成树：是原图的一个子图，它连接了原图中的所有节点，但没有任何环，且包含了最少的边。一个包含
n个节点的图，其生成树总是包含n-1条边。
而最小生成树，就是在所有可能的生成树中，所有边的权重之和最小的那一棵。
解决最小生成树问题的经典算法有两个：
- Prim 算法：从一个起始节点开始，逐步向外扩展，每次都选择连接已构建树和未加入树的权重最小的边。
- Kruskal 算法：将所有边按权重从小到大排序，然后依次选择边，只要这条边不会形成环，就将其加入到生成树中。
这类算法旨在找到一个连接图中所有顶点，且总边权值最小的子图，这个子图就是所谓的最小生成树。
Prim算法
Prim 算法用于找到一个加权连通图的最小生成树（Minimum Spanning Tree, MST）。最小生成树是图的一个子图，它连接了所有节点，且所有边的权重之和最小。
Prim 算法从一个任意的起始节点开始，逐步添加边，以构建一棵树。在每一步中，它都选择连接当前已构建树与未加入树的节点的权重最小的边。这个过程重复进行，直到所有节点都被加入到树中。
算法步骤
- 初始化：创建一个距离数组
dist，将起始节点的距离设为 0，其他节点的距离设为无穷大。这个距离表示节点与当前已构建树之间的最小边权。 - 优先队列：使用一个最小优先队列来存储
<边权, 节点>对，初始时将<0, 起始节点>放入队列。 - 循环：只要优先队列不为空，就执行以下操作：
- 从队列中弹出边权最小的节点
u。 - 如果
u已经被访问过，则跳过。 - 标记
u为已访问，并将边权weight加入到 MST 的总权重中。 - 遍历
u的所有邻接节点v：- 如果
v未被访问，并且边(u, v)的权重小于v当前的距离：- 更新
v的距离：dist[v] = weight(u, v)。 - 将
<weight(u, v), v>放入优先队列。
- 更新
- 如果
- 从队列中弹出边权最小的节点
- 结果：当循环结束时，所有节点的
dist值的总和（或者通过其他方式记录的边的权重之和）就是最小生成树的总权重。
适用场景
- 构建最小生成树，例如，设计一个网络连接所有城市，但要使总光缆长度最小。
- Prim 算法可以处理负权边，因为它只关心边本身的权重，而不是累积的路径权重。
prim算法核心就是三步，称为prim三部曲，大家一定要熟悉这三步，代码相对会好些很多：
- 第一步，选距离生成树最近节点
- 第二步，最近节点加入生成树
- 第三步，更新非生成树节点到生成树的距离
minDist数组是记录了所有非生成树节点距离生成树的最小距离。最后，minDist数组也就是记录的是最小生成树所有边的权值。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48// prim算法
using namespace std;
int main() {
int v,e;
cin>>v>>e;
vector<int> minDist(v+1,10001);
vector<vector<int>> grid(v+1,vector<int>(v+1,10001));
vector<bool> isIntree(v+1);
while(e--) {
int s,t,val;
cin>>s>>t>>val;
grid[s][t] = val;
grid[t][s] = val;
}
for(int i = 1;i<v;++i) {
// 添加n-1条边即可
int dist{numeric_limits<int>::max()};
int cur = -1;
for(int j = 1;j<=v;++j) {
// 找到非最小生成树的点距离最小生成树最小的点
if(!isIntree[j]&&minDist[j]<dist) {
dist = minDist[j];
cur = j;
}
}
// 找到距离最小生成树最小的点
// 加入最小生成树
isIntree[cur] = true;
// 更新距离
for(int j = 1;j<=v;++j){
if(!isIntree[j]&&minDist[j]>grid[cur][j]) {
// 当前节点距离cur的距离更小
minDist[j] = grid[cur][j]; // 距离也是添加的边
}
}
}
int result{};
for(int i = 2;i<=v;i++) {
// 计算距离
result+=minDist[i];
}
cout<<result<<'\n';
return 0;
}
如果需要记录最小生成树1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
using namespace std;
int main() {
int v, e;
int x, y, k;
cin >> v >> e;
// 填一个默认最大值，题目描述val最大为10000
vector<vector<int>> grid(v + 1, vector<int>(v + 1, 10001));
while (e--) {
cin >> x >> y >> k;
// 因为是双向图，所以两个方向都要填上
grid[x][y] = k;
grid[y][x] = k;
}
// 所有节点到最小生成树的最小距离
vector<int> minDist(v + 1, 10001);
// 这个节点是否在树里
vector<bool> isInTree(v + 1, false);
vector<int> parent(v+1,-1);
// 只需要循环 n-1次，建立 n - 1条边，就可以把n个节点的图连在一起
for (int i = 1; i < v; i++) {
// 1、prim三部曲，第一步：选距离生成树最近节点
int cur = -1; // 选中哪个节点 加入最小生成树
int minVal = INT_MAX;
for (int j = 1; j <= v; j++) { // 1 - v，顶点编号，这里下标从1开始
// 选取最小生成树节点的条件：
// （1）不在最小生成树里
// （2）距离最小生成树最近的节点
if (!isInTree[j] && minDist[j] < minVal) {
minVal = minDist[j];
cur = j;
}
}
// 2、prim三部曲，第二步：最近节点（cur）加入生成树
isInTree[cur] = true;
// 3、prim三部曲，第三步：更新非生成树节点到生成树的距离（即更新minDist数组）
// cur节点加入之后， 最小生成树加入了新的节点，那么所有节点到 最小生成树的距离（即minDist数组）需要更新一下
// 由于cur节点是新加入到最小生成树，那么只需要关心与 cur 相连的 非生成树节点 的距离 是否比 原来 非生成树节点到生成树节点的距离更小了呢
for (int j = 1; j <= v; j++) {
// 更新的条件：
// （1）节点是 非生成树里的节点
// （2）与cur相连的某节点的权值 比 该某节点距离最小生成树的距离小
// cur 是新加入 最小生成树的节点，那么 所有非生成树的节点距离生成树节点的最近距离 由于 cur的新加入，需要更新一下数据了
if (!isInTree[j] && grid[cur][j] < minDist[j]) {
minDist[j] = grid[cur][j];
parent[j] = cur; // 记录边 cur是加入二叉树的节点,如果j到cur的值更小,则记录边
}
}
}
// 统计结果
int result = 0;
for (int i = 2; i <= v; i++) { // 不计第一个顶点，因为统计的是边的权值，v个节点有 v-1条边
result += minDist[i];
}
cout << result << endl;
// 输出 最小生成树边的链接情况
for (int i = 1; i <= v; i++) {
cout << i << "->" << parent[i] << endl;
}
}
Kruskal算法
解决问题：最小生成树（MST）。
核心思想：这是一种贪心算法，也叫“加边法”。它总是选择全局最优的边来构建树。
工作流程：
- 将图中的所有边按权值从小到大排序。
- 遍历排序后的边，依次尝试将每条边加入最小生成树中。
- 在添加每条边之前，使用并查集（Union-Find）来检查这条边是否会形成一个环。
- 如果该边连接的两个顶点不在同一个集合中（即不会形成环），就接受这条边，并将这两个顶点所在的集合合并。
- 重复此过程，直到选择了
V-1条边（其中V是顶点数）。
优点：适用于稀疏图（边远少于顶点平方的图），实现相对简单
prim 算法是维护节点的集合，而 Kruskal 是维护边的集合。
上来就这么说，大家应该看不太懂，这里是先让大家有这么个印象，带着这个印象在看下文，理解的会更到位一些。
kruscal的思路：
- 边的权值排序，因为要优先选最小的边加入到生成树里
- 遍历排序后的边
- 如果边首尾的两个节点在同一个集合，说明如果连上这条边图中会出现环
- 如果边首尾的两个节点不在同一个集合，加入到最小生成树，并把两个节点加入同一个集合
1 |
|
Kruskal 与 prim 的关键区别在于，prim维护的是节点的集合，而 Kruskal 维护的是边的集合。 如果 一个图中，节点多，但边相对较少，那么使用Kruskal 更优。因为 Kruskal 是对边进行排序的后 进行操作是否加入到最小生成树。
边如果少，那么遍历操作的次数就少。
在节点数量固定的情况下，图中的边越少，Kruskal 需要遍历的边也就越少。
而 prim 算法是对节点进行操作的，节点数量越少，prim算法效率就越优。
所以在 稀疏图中，用Kruskal更优。 在稠密图中，用prim算法更优
Prim 算法 时间复杂度为 O(n^2)，其中 n 为节点数量，它的运行效率和图中边树无关，适用稠密图。
Kruskal算法 时间复杂度 为 nlogn，其中n 为边的数量，适用稀疏图
最小连接费用
给你一个points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。
连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 ：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。
请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时，才认为所有点都已连接。
最小生成树,使用Prim算法,首先使用邻接矩阵记录边值,不可达的设为最大值. 然后选择距离最小生成树距离最小的值(使用minDist记录每个点到最小生成树距离,初始化为两个节点间距离最大值+1,因为要通过INT_MAX找最小值,不能使用存INT_MAX),然后找到minDist中最小值(对应节点不能在最小生成树中,通过vector\ Kruskal算法,按边选择 并查集（Union-Find）是一种用于处理不相交集合（disjoint sets）的数据结构。它最主要的功能是： 需要判断两个元素是否在同一个集合里的时候，我们就要想到用并查集。 并查集主要有两个功能： 并查集的底层实现通常是基于一个数组或哈希表，其中每个元素都用一个父节点指针来表示。 在这个例子中， 并查集通过记录数组parent,也就是根节点实现 . 简单的实现方式在某些情况下可能会导致树变得非常高，使得 在 如果这棵多叉树高度很深的话，每次find函数 去寻找根的过程就要递归很多次。 我们的目的只需要知道这些节点在同一个根下就可以，所以对这棵多叉树的构造只将子节点父节点均指向同一元素即可.除了根节点其他所有节点都挂载根节点下，这样我们在寻根的时候就很快，只需要一步，如果我们想达到这样的效果，就需要 路径压缩，将非根节点的所有节点直接指向根节点。 只需要在递归的过程中，让 parent[u] 接住 递归函数 find(parent[u]) 的返回结果。因为 find 函数向上寻找根节点，parent[u] 表述 u 的父节点，那么让 parent[u] 直接获取 find函数 返回的根节点，这样就让节点 u 的父节点 变成根节点。 通过模板，可以知道并查集主要有三个功能。 判断两个节点是否在同一个集合，函数：isSame(int u, int v)，就是判断两个节点是不是同一个根节点 按秩合并（Union by Rank）或按大小合并（Union by Size） 在 通过这些优化，并查集的平均时间复杂度几乎可以达到常数级别，非常高效 将较小的树合并到较大的树上：这种策略可以最小化树的高度增长，从而保证并查集的高效性。 按秩合并代码如下,注意到在上面的模板代码中，没有做路径压缩的，因为一旦做路径压缩，rank记录的高度就不准了，根据rank来判断如何合并就没有意义。 也可以在 路径压缩的时候，再去实时修生rank的数值，但这样在代码实现上麻烦了不少，关键是收益很小。其实在优化并查集查询效率的时候，只用路径压缩的思路就够了，不仅代码实现精简，而且效率足够高。按秩合并的思路并没有将树形结构尽可能的扁平化，所以在整理效率上是没有路径压缩高的。 路径压缩后的并查集时间复杂度在O(logn)与O(1)之间，且随着查询或者合并操作的增加，时间复杂度会越来越趋于O(1)。在第一次查询的时候，相当于是n叉树上从叶子节点到根节点的查询过程，时间复杂度是logn，但路径压缩后，后面的查询操作都是O(1)，而 join 函数 和 isSame函数 里涉及的查询操作也是一样的过程。在第一次查询的时候，相当于是n叉树上从叶子节点到根节点的查询过程，时间复杂度是logn，但路径压缩后，后面的查询操作都是O(1)，而 join 函数 和 isSame函数 里涉及的查询操作也是一样的过程空间复杂度： O(n) ，申请一个parent数组。 拓扑排序（Topological Sort）是对有向无环图（DAG, Directed Acyclic Graph）的顶点进行的一种线性排序。这种排序的结果是一个序列，其中每个顶点都排在其所有依赖它的顶点之前。 简单来说，拓扑排序就是为了解决任务调度问题而生的：如果你有一系列相互依赖的任务，拓扑排序能给你一个合理的执行顺序。 拓扑排序的核心思想是，在一个有向图中，总会存在一个或多个入度为零（没有其他顶点指向它）的顶点。这些顶点可以作为任务序列的起始 最常见、也最直观的拓扑排序算法。 做拓扑排序的时候，应该优先找 入度为 0 的节点，只有入度为0，它才是出发节点。 理解以上内容很重要！ 接下来我给出 拓扑排序的过程，其实就两步： 某个大型软件项目的构建系统拥有 N 个文件，文件编号从 0 到 N - 1，在这些文件中，某些文件依赖于其他文件的内容，这意味着如果文件 A 依赖于文件 B，则必须在处理文件 A 之前处理文件 B （0 <= A, B <= N - 1）。请编写一个算法，用于确定文件处理的顺序。 发现结果集元素个数不等于 图中节点个数，就可以认定图中一定有有向环.这也是拓扑排序判断有向环的方法。 现在你总共有 返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回 任意一种 就可以了。如果不可能完成所有课程，返回 一个空数组 。 此外还有基于 DFS 的拓扑排序,利用了递归的特性。 注意：在基于 DFS 的方法中，如果递归过程中发现一个“访问中”的顶点，说明图中存在环，无法进行拓扑排序。 二分图 定义：如果能将一个图的节点集合分割成两个独立的子集 存在一个 无向图 ，图中有 二分图 定义：如果能将一个图的节点集合分割成两个独立的子集 如果图是二分图，返回 有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。 省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。 给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。 返回矩阵中 省份 的数量。 要解决这个问题，我们可以将城市和它们之间的连接关系看作是一个图（Graph）。其中，每个城市都是图中的一个节点，如果两个城市相连，那么它们之间就有一条边。题目中定义的“省份”其实就是图中的连通分量（Connected Component）。 因此，问题的核心就变成了：给定一个图，找出其中的连通分量数量。 我们可以使用两种常见的图遍历算法来解决这个问题：深度优先搜索（DFS）或广度优先搜索（BFS）。 方法一：深度优先搜索（DFS） DFS 的基本思想是从一个未访问过的城市开始，沿着它的连接路径一直走下去，直到所有与之相连的城市都被访问。当这条路径走完后，我们就找到了一个完整的省份。然后，我们从下一个未访问过的城市重新开始，重复这个过程，直到所有城市都被访问。 算法步骤： 代码实现 方法二：广度优先搜索（BFS） BFS 的思想与 DFS 类似，只是遍历的方式不同。它不是沿着一条路径一直走，而是从一个城市开始，先访问所有与它直接相连的城市，然后是与这些城市直接相连的城市，以此类推。我们可以使用队列（Queue）来实现 BFS。 算法步骤： 回溯（Backtracking）是一种通过探索所有可能的候选解来找出所有解或最优解的算法策略。它通常用于解决组合问题、排列问题、子集问题等。 回溯算法的本质是深度优先搜索 (DFS) 的一种特殊应用。它像是在一个解空间树中进行遍历，每走一步就尝试一个选择，如果发现当前选择不能达到目标或偏离了最佳路径，就会“回溯”（撤销当前选择），退回到上一步，然后尝试另一个选择。 这个过程可以概括为：选择 → 探索 → 撤销。 掌握这三要素是编写回溯代码的关键： 路径 (Path): 记录已经做出的选择。这通常是一个 选择列表 (Choices): 当前可以做出的选择。这是从问题中抽象出来的，通常是某个集合或数组中剩余的元素。 结束条件 (Base Case / Termination Condition): 什么时候停止递归？通常是路径满足了特定条件（比如长度达到要求，找到了一个解）或者选择列表为空。 状态修改 参数传递： 通常， 状态的“做选择”和“撤销选择”： 确保每做一步选择后，都将其添加到 剪枝是回溯算法的灵魂，能极大提高效率。 定义： 在搜索过程中，一旦发现当前路径不可能得到有效解或最优解时，就立即停止对该路径的后续搜索。 常见剪枝点： 当输入数组中包含重复元素，但要求结果中不允许有重复的组合/排列时，去重是一个常见的难点。 遍历方式的选择 是否允许重复选择元素： 允许（例如组合问题， 不允许（例如排列问题，每个元素只能用一次）： 递归时，需要通过 是否要求组合/排列： 常见回溯问题类型 回溯法也可以叫做回溯搜索法，它是一种搜索的方式,回溯是递归的副产品，只要有递归就会有回溯 回溯的本质是穷举，穷举所有可能，然后选出想要的答案，如果想让回溯法高效一些，可以加一些剪枝的操作，但也改不了回溯法就是穷举的本质。 回溯法解决的问题都可以抽象为树形结构，因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度就构成了树的深度。 递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。 回溯法，一般可以解决如下几种问题： 回顾一下,递归算法的三个要素。每次写递归，都按照这三要素来写 回溯算法的核心思想可以概括为两个字：穷举。它通过递归的方式，系统性地探索所有可能的路径，直到找到问题的解。但为了提高效率，它会结合剪枝（pruning）技术，提前排除那些不可能得到解的路径。回溯 = 递归 + 剪枝 回溯三部曲 在回溯算法中，函数起名字为backtracking，回溯算法中函数返回值一般为void。 再来看一下参数，因为回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来，所以一般是先写逻辑，然后需要什么参数，就填什么参数。 确定“路径”和“选择列表” 在递归函数中，这两个要素通常作为函数的参数传入 什么时候达到了终止条件，树中就可以看出，一般来说搜到叶子节点了，也就找到了满足条件的一条答案，把这个答案存放起来，并结束本层递归。 当满足某个条件时，递归必须停止。这通常意味着你已经找到了一个完整的解。 超出边界：当路径的长度达到问题的要求，或者无法再做任何选择时，递归终止 回溯搜索的遍历过程 回溯法一般是在集合中递归搜索，集合的大小构成了树的宽度，递归的深度构成的树的深度。 实现回溯的核心，它通常包含以下三个步骤： 从图中看出for循环可以理解是横向遍历，backtracking（递归）就是纵向遍历，这样就把这棵树全遍历完了，一般来说，搜索叶子节点就是找的其中一个结果了。 给定两个整数 你可以按 任何顺序 返回答案。 使用startIndex避免重复,这个参数用来记录本层递归的中，集合从哪里开始遍历（集合就是[1,…,n] ）。 这道题目还可以进一步减枝,可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。如果for循环选择的起始位置之后的元素个数已经不足需要的元素个数了，那么就没有必要搜索了 看一下优化过程如下： 为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。 找出所有相加之和为 返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。 回溯三部曲: 确定递归函数参数,依然需要一维数组path来存放符合条件的结果，二维数组result来存放结果集。接下来还需要如下参数： targetSum（int）目标和，也就是题目中的n。 k（int）就是题目中要求k个数的集合。 sum（int）为已经收集的元素的总和，也就是path里元素的总和。 startIndex（int）为下一层for循环搜索的起始位置。 回溯法中递归函数参数很难一次性确定下来，一般先写逻辑，需要什么参数填什么参数。 确定终止条件 什么时候终止呢？k其实就已经限制树的深度，因为就取k个元素，树再往下深了没有意义。 所以如果path.size() 和 k相等了，就终止。 如果此时path里收集到的元素和（sum） 和targetSum（就是题目描述的n）相同了，就用result收集当前的结果。 单层搜索过程 处理过程就是 path收集每次选取的元素，相当于树型结构里的边，sum来统计path里元素的总和。 剪支逻辑类似,从深度和广度上考虑. 从递归深度上,如果sum>n则可以退出,从选择范围来看,类似上一个题目,i<=9-(k-r.size())+1. 把问题抽象为树形结构，按照回溯三部曲解，最后给出剪枝的优化 给定一个仅包含数字 给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。 给你一个 无重复元素 的整数数组 对于给定的输入，保证和为 回溯三部曲: 这里依然是定义两个全局变量，二维数组result存放结果集，数组path存放符合条件的结果。（这两个变量可以作为函数参数传入） 首先是题目中给出的参数，集合candidates, 和目标值target。 此外我还定义了int型的sum变量来统计单一结果path里的总和，其实这个sum也可以不用，用target做相应的减法就可以了，最后如何target==0就说明找到符合的结果了，但为了代码逻辑清晰，我依然用了sum。还需要startIndex来控制for循环的起始位置，对于组合问题，如果是一个集合来求组合的话，就需要startIndex，如果是多个集合取组合，各个集合之间相互不影响，那么就不用startIndex 从叶子节点可以清晰看到，终止只有两种情况，sum大于target和sum等于target。 sum等于target的时候，需要收集结果 单层for循环依然是从startIndex开始，搜索candidates集合。本题元素为可重复选取的,递归时startIndex不需要+1. 剪枝优化,对于sum已经大于target的情况，其实是依然进入了下一层递归，只是下一层递归结束判断的时候，会判断sum > target的话就返回。在for循环的搜索范围上做做文章了。 对总集合排序之后，如果下一层的sum（就是本层的 sum + candidates[i]）已经大于target，就可以结束本轮for循环的遍历。在求和问题中，排序之后加剪枝是常见的套路 给定一个候选人编号的集合 注意：解集不能包含重复的组合。 这道题目和上一题组合总和如下区别： 本题的难点在于区别2中：集合（数组candidates）有重复元素，但还不能有重复的组合,使用set去重会超时.所以要在搜索的过程中就去掉重复组合 给你一个字符串 涉及到两个关键问题： 切割问题类似组合问题。 例如对于字符串abcdef： 全局变量数组path存放切割后回文的子串，二维数组result存放结果集。 （这两个参数可以放到函数参数里）本题递归函数参数还需要startIndex，因为切割过的地方，不能重复切割，和组合问题也是保持一致的 从树形结构的图中可以看出：切割线切到了字符串最后面，说明找到了一种切割方法，此时就是本层递归的终止条件。 来看看在递归循环中如何截取子串呢？ 在 首先判断这个子串是不是回文，如果是回文，就加入在 可以先通过动态规划得到字串是否是回文字串 也可以先动态规划计算字串是否是回文字符串 给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。 有效的 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 ‘.’ 分隔。 切割问题类似组合问题。startIndex一定是需要的，因为不能重复分割，记录下一层递归分割的起始位置。本题我们还需要一个变量pointNum，记录添加逗点的数量。 终止条件和分割回文串情况就不同了，本题明确要求只会分成4段，所以不能用切割线切到最后作为终止条件，而是分割的段数作为终止条件。pointNum表示逗点数量，pointNum为3说明字符串分成了4段了。然后验证一下第四段是否合法，如果合法就加入到结果集里 在 然后就是递归和回溯的过程：递归调用时，下一层递归的startIndex要从i+2开始（因为需要在字符串中加入了分隔符 给你一个整数数组 解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。 如果把 子集问题、组合问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点.子集也是一种组合问题，因为它的集合是无序的，子集{1,2} 和 子集{2,1}是一样的。那么既然是无序，取过的元素不会重复取，写回溯算法的时候，for就要从startIndex开始，而不是从0开始 全局变量数组path为子集收集元素，二维数组result存放子集组合。（也可以放到递归函数参数里） 递归函数参数在上面讲到了，需要startIndex。 剩余集合为空的时候，就是叶子节点。 那么什么时候剩余集合为空呢？ 就是startIndex已经大于数组的长度了，就终止了，因为没有元素可取了 求取子集问题，不需要任何剪枝！因为子集就是要遍历整棵树。 给你一个整数数组 解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。 给你一个整数数组 数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。 核心是得到的结果不重复,同层使用过的元素不再使用.在之前组合总和中,使用排序+nums[i]!=nums[i-1]解决,而这里由于需要求递增序列不能再排序.所以可以通过哈希记录. 在子集II中是通过排序，再加一个标记数组(标记本树枝是否用过)来达到去重的目的。 而本题求自增子序列，是不能对原数组进行排序的，排完序的数组都是自增子序列了。 所以不能使用之前的去重逻辑！ 给定一个不含重复数字的数组 首先排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前的子集以及组合所不同的地方。 可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。但排列问题需要一个used数组，标记已经选择的元素 可以看出叶子节点，就是收割结果的地方。当收集元素的数组path的大小达到和nums数组一样大的时候，说明找到了一个全排列，也表示到达了叶子节点。 for循环里不用startIndex了。因为排列问题，每次都要从头开始搜索，例如元素1在[1,2]中已经使用过了，但是在[2,1]中还要再使用一次1。而used数组，其实就是记录此时path里都有哪些元素使用了，一个排列里一个元素只能使用一次 给定一个可包含重复数字的序列 给你一份航线列表 所有这些机票都属于一个从 假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。 使用dfs,到达一个点后删除该条边. 按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 n 皇后问题 研究的是如何将 给你一个整数 每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 path设置为vector\ 编写一个程序，通过填充空格来解决数独问题。 数独的解法需 遵循如下规则： 数独部分空格内已填入了数字，空白格用 核心思想：分治,快速排序主要分为三个步骤： 分区操作是快速排序的核心。目标是将数组 Lomuto 分区方案： Hoare 分区方案： 归并排序（Merge Sort）是一种高效的、基于分治（Divide and Conquer）思想的排序算法。它的核心思想是将一个大问题分解成若干个小问题，直到小问题足够简单可以直接解决，然后将这些小问题的解合并起来，从而解决原先的大问题。 归并排序主要分为两个核心步骤： 前缀树（Trie），又称“字典树”，是一种用于高效存储和查找字符串集合的树形数据结构。它的核心思想是利用字符串的公共前缀来减少查询时间。 前缀树的核心知识 一个前缀树由一系列节点组成，每个节点通常包含以下信息： 前缀树的查找和插入操作都非常直观： 如何实现前缀树(包括插入,查找，前缀查找)并利用前缀树进行单词查找. 掌握了前缀树的原理后，我们可以用它来解决一些 LeetCode 上的经典问题。 1. 实现前缀树 (Trie) 这是最基础的题目，要求你实现 这道题需要你在一个网格中找出所有符合条件的单词。如果对每个单词都进行独立的搜索，效率会很低。使用前缀树可以大大优化。 这道题要求你实现一个字典，支持插入键值对和计算具有某个前缀的所有键对应值的总和。 前缀树在处理与字符串前缀相关的查找、插入、计数等问题时，是一种非常高效且优雅的解决方案。 有三根柱子A,B,C. 有n个盘子从大到小放在A柱子上,小盘子必须在大盘子上面,要求移动到C柱子. 时间复杂度O(2^n -1) c++的STL相比于java集合的使用没有那么简单,迭代器以及一些容器类的使用更加晦涩. 这里介绍一些常用类,常用方法以及注意事项,还有一些没那么常见的类也要看一看注意一下. 使用c++STL需要注意的点是容器本身的方法和std下提供的算法的不同,比如参数是size_type还是iter_pos,以及返回值是迭代器还是size_type. std::find以及string.find,map.find等差别.erase返回值的差别 很常用容器,支持随机访问以及尾部增删 注意它没有find方法,因为可以使用遍历方便查找,或者使用std::find. 当 常见的引起重新分配的操作： 注意事项： 在需要删除满足特定条件的所有元素时，通常不直接在循环中使用 功能：请求 注意事项：如果 主要是insert,erase的返回值,vector的insert,erase操作只能是迭代器并返回操作成功指向的迭代器(insert返回指向的插入成功的迭代器,erase返回指向删除后的下一个迭代器) 而string的insert和erase的重载方法中有参数是索引,返回值是指向字符串自身的引用,也就是说可以链式调用. 并且注意,erase的第一个参数是offset,第二个参数是删除个数,默认一直删到末尾. 类似的参数还有substr,第一个参数是offset,第二个参数是limit. 此外erase,insert也有对应参数为迭代器的重载 迭代器失效： 大多数 性能开销： 在字符串的中间或开头进行插入操作，通常需要移动大量现有字符，这会带来较大的性能开销。如果性能是关键考虑因素，并且需要频繁在中间插入，你可能需要重新评估数据结构或算法。 字符串查找可以使用find,返回值是索引 作用： 在字符串中查找子串或字符。 还有个replace方法可能容易忽略,能替换字符串 一般注意事项： list是双向链表,在链表两端增删数据效率O(1),但查询需要遍历,而deque支持随机访问. 快速插入/删除： 在列表的任何位置进行插入和删除操作都是常数时间复杂度 O(1)，因为只需要修改少量指针。 不支持随机访问： 无法通过索引 迭代器稳定性： 插入和删除操作不会使其他迭代器失效（除了被删除的元素对应的迭代器）。 内存开销： 每个元素除了存储数据本身，还需要额外的内存来存储前后指针，因此比 头部/尾部快速插入/删除： 随机访问： 支持通过索引 中部插入/删除： 在中部插入和删除元素是线性时间复杂度 O(n)，因为可能需要移动元素。 迭代器稳定性： 内存使用： 比 构造函数 (Constructors) 注意队列有q.back获得队尾元素,而栈只能访问一端,也就是栈顶. 在map/set以及unordered_map/unordered_set中,erase成员方法参数如果是size_type,返回值是删除个数,如果是迭代器或者迭代器范围,返回值指向下一个元素迭代器. 而find通过值返回迭代器. 而在string中,erase参数是offset与len,返回指向新字符串的引用,find参数是字符或字符串返回size_type索引. 而在vector,list中,erase参数是迭代器或者迭代器范围,返回删除成功后指向的下一个元素迭代器,而没有find成员方法. 功能： 使用指定的底层容器类型 返回值： 无。 示例 (最小堆 - Min-Heap)： 这里， set同理. 而 std::vector 关键在于它们底层的实现机制不同： 需要键是可哈希的（通过 操作的平均时间复杂度是 O(1)。 如果vector,string等作为map的key,然后对这个key进行了操作会怎样. 如果 如果你修改了这个 此时，红黑树的内部结构就会变得不一致 (corrupted)。树的节点仍然按照旧的键值进行组织，但实际的键值已经改变，导致查找、插入、删除等操作都会出错，因为它们会根据错误的顺序进行导航。最终结果就是未定义行为，程序可能崩溃，也可能产生错误的结果。 multimap/unordered_multimap multiset/unordered_multiset 核心特点 核心特点 这是一个非常典型的 Undefined Behavior (UB) 警告/错误，通常由 Clang/LLVM 编译器（或其衍生的 sanitizers，如 AddressSanitizer/ASan）在运行时检测到。 为什么会发生这种错误？ 无效的索引或指针算术： 例如： 或者更直接的： 减法错误导致无符号数溢出： 例如： 内存越界访问： Line 1122: Char 9: runtime error: reference binding to null pointer of type ‘int’ (stl_vector.h) 遇到的这个 虽然错误信息指向 这个错误最常见的根本原因就是：你试图通过 具体来说，当 欢迎关注我的其它发布渠道1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46class Solution {
public:
int minCostConnectPoints(vector<vector<int>>& points) {
//Prim 计算图的最小生成树 也就是连通的最小权重
int n = points.size();
vector<bool> isInTree(n); // 是否在树中
vector<vector<int>> grid(n,vector<int>(n));
int maxdist{};
for(int i = 0;i<n;++i) {
for(int j = i+1;j<n;++j) {
int dis = abs(points[i][0] - points[j][0]) + abs(points[i][1] - points[j][1]);
grid[i][j] = dis;
grid[j][i] = dis;
maxdist = max(maxdist,dis);
}
}
vector<int> minDist(n,maxdist+1);
for(int i = 0;i<n-1;++i) {
// 选择n-1个值
int dis{numeric_limits<int>::max()}; //选择距离最小生成树的点
int cur = -1;
for(int j = 0;j<n;++j) {
if(!isInTree[j]&&minDist[j]<dis) {
dis = minDist[j];
cur = j;
}
}
// 选择cur进入最小生成树
isInTree[cur] = true;
// 更新最短距离
for(int j = 0;j<n;j++) {
if(!isInTree[j]&&minDist[j]>grid[cur][j]) {
minDist[j] = grid[cur][j];
// 如果要看边 可以记录边
// parent[j] = cur;
}
}
}
int result{};
for(int i = 1;i<n;++i) {
result += minDist[i];
}
return result;
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60class Solution {
public:
vector<int> parent;
void init(int n) {
parent.resize(n);
for (int i = 0; i < n; ++i) {
parent[i] = i;
}
}
typedef struct Edge { int l, r, val; } Edge;
int find(int n) { return n == parent[n] ? n : parent[n] = find(parent[n]); }
void join(int i, int j) {
i = find(i);
j = find(j);
if (i == j)
return;
parent[i] = j;
}
bool isSame(int i, int j) {
i = find(i);
j = find(j);
return i == j;
}
int minCostConnectPoints(vector<vector<int>>& points) {
// Kruskal
int n = points.size();
vector<Edge> edges;
vector<vector<int>> grid(n, vector<int>(n, numeric_limits<int>::max()));
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
int dis = abs(points[i][0] - points[j][0]) +
abs(points[i][1] - points[j][1]);
edges.push_back({i, j, dis});
}
}
// 按权重排序边
sort(edges.begin(), edges.end(),
[](const Edge& a, const Edge& b) { return a.val < b.val; });
// 初始化并查集
init(n);
int result{};
// 选择权重最小的边,看是否在同一集合
for (int i = 0; i < edges.size(); ++i) {
auto e = edges[i];
int x = e.l;
int y = e.r;
int v = e.val;
if (isSame(x, y)) {
// 同一集合
// 不加入 加入后形成环
continue;
} else {
join(x, y);
result += v;
}
}
return result;
}
};总结与对比
算法 类型 解决问题 适用场景 核心思想 Dijkstra 最短路径 单源最短路径 非负权图 贪心，逐步扩展最近点 Floyd-Warshall 最短路径 所有顶点对最短路径 正负权图（无负权环） 动态规划，考虑所有中间点 Kruskal 最小生成树 最小生成树 稀疏图 贪心，按边排序，用并查集防环 Prim 最小生成树 最小生成树 稠密图 贪心，按点扩展，用优先队列找最近边 并查集
parent 来存储每个元素的父节点。parent[i] 存储的是元素 i 的父节点的索引。parent[i] == i。这个根节点就是该集合的代表。Find 操作的实现Find(x) 操作就是从元素 x 开始，沿着父节点指针一直向上追溯，直到找到根节点。1
2
3
4元素 0 -> 1 -> 3
^ ^
| |
根节点 4 <- 2 <- 5Find(0) 会返回 3，因为 3 是 0 的根节点。Find(2) 会返回 4，Find(5) 也返回 4。Union 操作的实现Union(x, y) 操作就是将元素 x 所在的集合和元素 y 所在的集合合并。最简单的方法是找到 x 和 y 的根节点 root_x 和 root_y，然后将 root_y 的父节点设为 root_x。1
2
3
4// Union(0, 2)
1. 找到 0 的根节点: 3
2. 找到 2 的根节点: 4
3. 将 4 的父节点设为 31
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21并查集常用操作
找到根节点
// 并查集里寻根的过程
int find(int u) {
if (u == father[u]) return u; // 如果根就是自己，直接返回
else return find(father[u]); // 如果根不是自己，就根据数组下标一层一层向下找
}
// 查找是否同一集合
// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
// 将v，u 这条边加入并查集
void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (u == v) return; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
father[v] = u;
}并查集优化
Find 操作的效率降低。因此，有两个经典的优化方法：Find 操作中，当我们找到根节点时，可以将路径上所有节点的父节点都直接指向根节点。这会极大地扁平化树的结构，使得后续的 Find 操作更快。1
2
3
4
5// 并查集里寻根的过程
int find(int u) {
if (u == father[u]) return u;
else return father[u] = find(father[u]); // 路径压缩
}Union 操作中，为了保持树的平衡，我们总是将较小的树合并到较大的树上。这可以防止树变得过高。Find 操作的平均路径长度不会显著增加。一定是 rank 小的树合入 到 rank大 的树，这样可以保证最后合成的树rank 最小，降低在树上查询的路径长度。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33int n = 1005; // n根据题目中节点数量而定，一般比节点数量大一点就好
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构
vector<int> rank = vector<int> (n, 1); // 初始每棵树的高度都为1
// 并查集初始化
void init() {
for (int i = 0; i < n; ++i) {
father[i] = i;
rank[i] = 1; // 也可以不写
}
}
// 并查集里寻根的过程
int find(int u) {
return u == father[u] ? u : find(father[u]);// 注意这里不做路径压缩
}
// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (rank[u] <= rank[v]) father[u] = v; // rank小的树合入到rank大的树
else father[v] = u;
if (rank[u] == rank[v] && u != v) rank[v]++; // 如果两棵树高度相同，则v的高度+1，因为上面 if (rank[u] <= rank[v]) father[u] = v; 注意是 <=
}拓扑排序
u，并将其添加到结果序列中。 b. 更新入度：遍历顶点 u 的所有邻接点 v，将它们的入度减一。 c. 入队：如果某个邻接点 v 的入度变为零，将其放入队列。软件构建
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
using namespace std;
int main() {
int n,m;
cin>>n>>m;
vector<int> deg(n);
vector<vector<int>> grid(n); // 也可以使用unordered_map<int,int>记录依赖关系
for(int i = 0;i<m;++i) {
int s,t;
cin>>s>>t;
deg[t]++;
grid[s].push_back(t);
}
queue<int> q;
vector<int> r;
for(int i = 0;i<n;++i) {
if(deg[i] == 0) {
q.push(i); // 入度为0 加入
}
}
while(!q.empty()) {
auto s = q.front();
q.pop();
r.push_back(s);
// 减少指向元素的度
for(auto t:grid[s]) {
deg[t]--;
if(deg[t] == 0) {
q.push(t);
}
}
}
if(r.size()<n) {
cout<<-1;
return 0;
}
for(int i = 0;i<r.size();++i) {
if(i == r.size()-1) {
cout<<r[i];
}else{
cout<<r[i]<<' ';
}
}
return 0;
}课程表II
numCourses 门课需要选，记为 0 到 numCourses - 1。给你一个数组 prerequisites ，其中 prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前 必须 先选修 bi 。0 ，你需要先完成课程 1 ，我们用一个匹配来表示：[0,1] 。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40class Solution {
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
// 统计入度
vector<vector<int>> grid(numCourses);
vector<int> indegrees(numCourses);
for (auto pre : prerequisites) {
indegrees[pre[0]]++; // b->a 1->0
grid[pre[1]].push_back(pre[0]);
}
// 从入度为0的开始 加入队列
queue<int> q;
for (int i = 0; i < numCourses; ++i) {
if (indegrees[i] == 0) {
q.push(i);
}
}
vector<int> result;
while (!q.empty()) {
auto s = q.front();
q.pop();
result.push_back(s);
// 弹出元素 并将指向的元素入度-1
for (auto t : grid[s]) {
indegrees[t]--;
if (indegrees[t] == 0) {
// 入度为0 加入堆
q.push(t);
}
}
}
if(result.size()<numCourses) {
return {};
}else{
return result;
}
}
};u： a. 将 u 标记为“访问中”。 b. 递归访问 u 的所有未访问的邻接点 v。 c. 回溯时入栈：当一个顶点的所有邻接点都被访问完毕（或无路可走）时，将该顶点压入栈。二分图
A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为 二分图 。判断二分图
n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：graph[u] 不包含 u）。graph[u] 不包含重复值）。v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）u 和 v 之间可能不存在一条连通彼此的路径。A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为 二分图 。true ；否则，返回 false1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60class Solution {
public:
bool dfs(vector<vector<int>>& graph,vector<int>& color,int n) {
for(int t:graph[n]) {
if(color[t] == color[n]) {
// 相同颜色
return false;
}
if(color[t] == 0){
// 未访问 设置颜色
color[t] = -color[n];
if(!dfs(graph,color,t)) {
return false;
}
}
}
return true;
}
bool isBipartite(vector<vector<int>>& graph) {
// 给节点染色
int n = graph.size();
vector<int> color(n);
queue<int> q;
for(int i = 0;i<n;++i) {
if(color[i] == 0) {
color[i] = 1;
if(!dfs(graph,color,i)) {
return false;
}
}
}
return true;
// for (int i = 0; i < n; ++i) {
// if (color[i] == 0) {
// q.push(i);
// color[i] = 1;
// }
// while (!q.empty()) {
// auto t = q.front();
// q.pop();
// // 找到相邻的点
// int val = color[t];
// for (int nx : graph[t]) {
// if (color[nx] == 0) {
// // 没有设置颜色 没有访问
// color[nx] = -val;
// q.push(nx);
// } else {
// // 已经访问过
// if (val == color[nx]) {
// // 值相同 说明出错
// return false;
// }
// }
// }
// }
// }
// return true;
}
};深搜广搜
连通分量
省份数量
count = 0，用于记录省份的数量。visited，大小为 n，用于标记城市是否已被访问。i = 0 到 n - 1。i：visited[i] 为 false，说明我们遇到了一个新省份。count 加 1。i 开始遍历，并标记所有与其相连的城市为已访问。i 作为参数。visited[i] 设置为 true。j，从 0 到 n - 1。i 与城市 j 相连（isConnected[i][j] == 1），且城市 j 未被访问（!visited[j]），则递归调用 DFS 函数，从城市 j 继续遍历。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution {
public int findCircleNum(int[][] isConnected) {
int n = isConnected.length;
boolean[] visited = new boolean[n];
int count = 0;
for (int i = 0; i < n; i++) {
if (!visited[i]) {
// 找到一个新的省份
count++;
// 从当前城市开始，深度遍历所有相连的城市
dfs(isConnected, visited, i);
}
}
return count;
}
private void dfs(int[][] isConnected, boolean[] visited, int i) {
// 标记当前城市为已访问
visited[i] = true;
// 遍历所有城市
for (int j = 0; j < isConnected.length; j++) {
// 如果城市i和城市j相连，且城市j未被访问过
if (isConnected[i][j] == 1 && !visited[j]) {
// 递归地继续遍历
dfs(isConnected, visited, j);
}
}
}
}count = 0 和布尔数组 visited。i：visited[i] 为 false，则 count++。i 加入队列。visited[i] 设置为 true。currentCity。j：currentCity 与城市 j 相连，且城市 j 未被访问，则将 j 加入队列，并将 visited[j] 设置为 true。重新规划路线
除法求值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52class Solution {
public:
double dfs(const unordered_map<string,unordered_map<string,double>>& graph,string x,string z,set<string>& visited) {
if(graph.find(x) == graph.end() || visited.count(x)) {
return -1.0; // 没有找到
}
// 如果找到了终点，返回 1.0 (表示从自己到自己的权重)
if (x == z) {
return 1.0;
}
visited.insert(x);
for(auto node:graph.at(x)) {
double result = dfs(graph,node.first,z,visited);
if(result != -1.0) {
return result*node.second; // 找到对应值
}
}
return -1.0;
}
vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
//1. 构建已有的图
unordered_map<string,unordered_map<string,double>> graph;
for(int i = 0;i<equations.size();++i) {
auto equation = equations.at(i);
string x = equation[0];
string y = equation[1];
graph[x][y] = values[i];
graph[y][x] = 1.0/values[i];
}
//2.dfs
vector<double> result;
for(auto query:queries) {
string x = query[0];
string y = query[1];
if(graph.find(x) == graph.end() || graph.find(y) == graph.end()) {
// 不存在该变量
result.emplace_back(-1.0);
}else if(x == y) {
// 值相等
result.emplace_back(1.0);
}else {
// 通过dfs查找值
set<string> visited;
result.emplace_back(dfs(graph,x,y,visited));
}
}
return result;
}
};回溯
List 或 Vector，存储当前已选择的元素。path 应该作为引用（或指针）传递，因为它在递归过程中需要被修改和回溯。其他参数根据是否需要在递归调用中改变而定。path 中；在递归调用结束后，务必撤销这个选择，恢复到递归前的状态，以便尝试其他分支。这是回溯算法的核心。if (i > start && nums[i] == nums[i-1]) continue;：这是最经典的去重技巧。for 循环遍历 Choices 时，检查当前元素是否与前一个元素相同。如果相同，并且前一个元素已经被跳过（而不是本次递归中被选择后移除的），则跳过当前元素，以避免生成重复的路径。[1,1,2] 选两个，可以是 [1,1]）： 递归时，下一个选择的起始索引可以从当前选择的索引开始 (i 或 startIndex)。visited 数组或移除元素的方式，确保元素不被重复选择。[1,2] 和 [2,1] 视为同一种）。通常通过在递归时传递一个 startIndex 参数来确保选择的元素索引是递增的，避免生成重复的组合。[1,2] 和 [2,1] 视为不同种）。通常需要一个 visited 数组或类似机制来标记已使用的元素。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23// Java 示例
void backtrack(参数, ... Path, Choices) {
// 1. 结束条件：满足某个条件时，将Path加入结果集，并返回
if (满足结束条件) {
result.add(new ArrayList<>(Path)); // 注意：这里通常需要拷贝Path，因为Path后续还会被修改
return;
}
// 2. 遍历所有选择
for (选择 in Choices) {
// 做选择：将当前选择加入Path
Path.add(选择);
// 剪枝（可选）：如果当前选择明显不符合条件，提前终止分支
// if (...) continue; 或 return;
// 递归：进入下一个决策层
backtrack(参数, ... Path, newChoices); // newChoices通常是基于当前选择更新后的
// 撤销选择：从Path中移除当前选择，回到上一个状态
Path.remove(Path.size() - 1);
}
}Subsets）。Combinations Sum, Combinations）。Permutations）。Word Search, N-Queens）。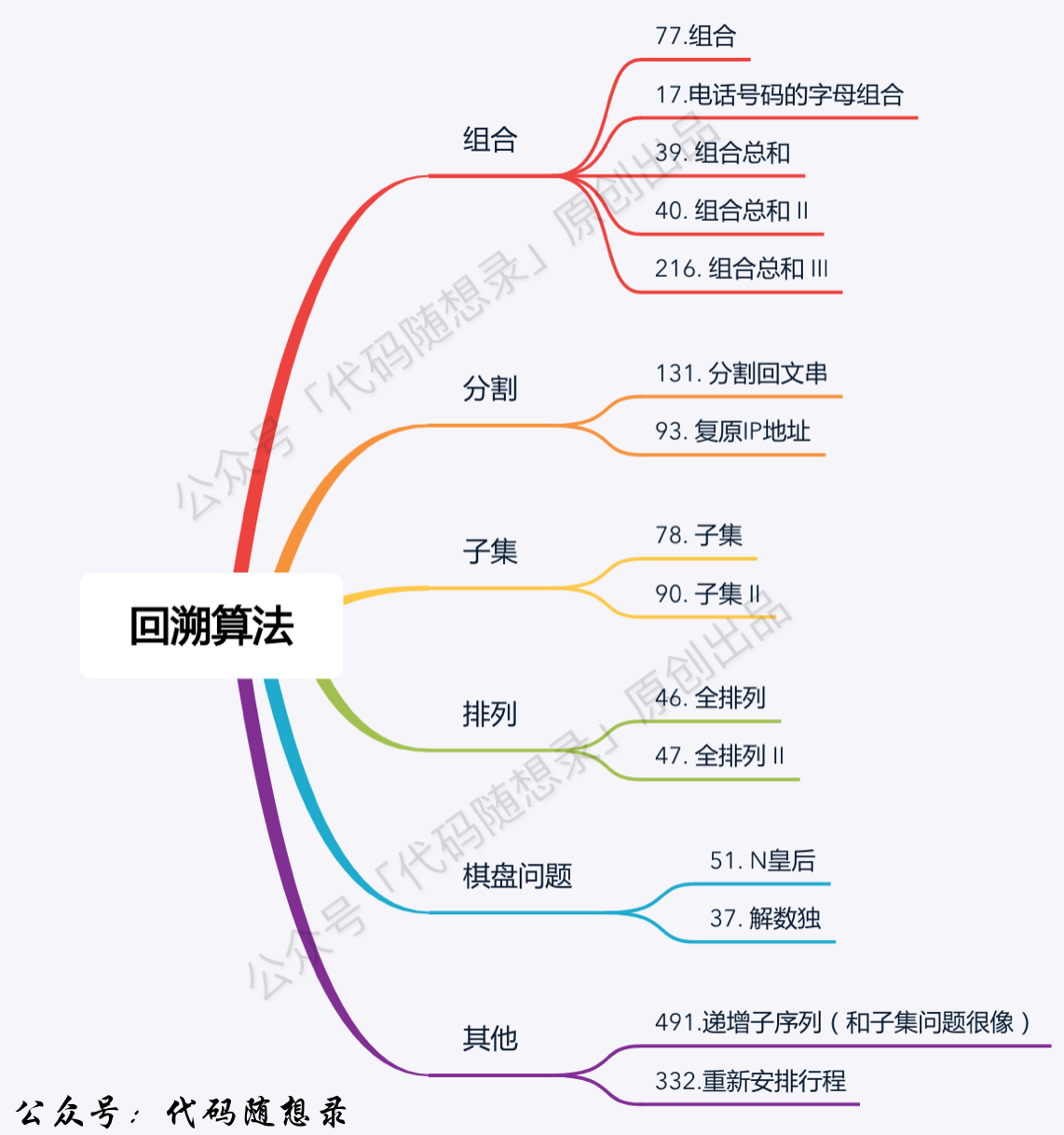
1
2
3
4
5
6
7
8
9
10
11
12
13void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
处理节点;
backtracking(路径，选择列表); // 递归
回溯，撤销处理结果
}
}
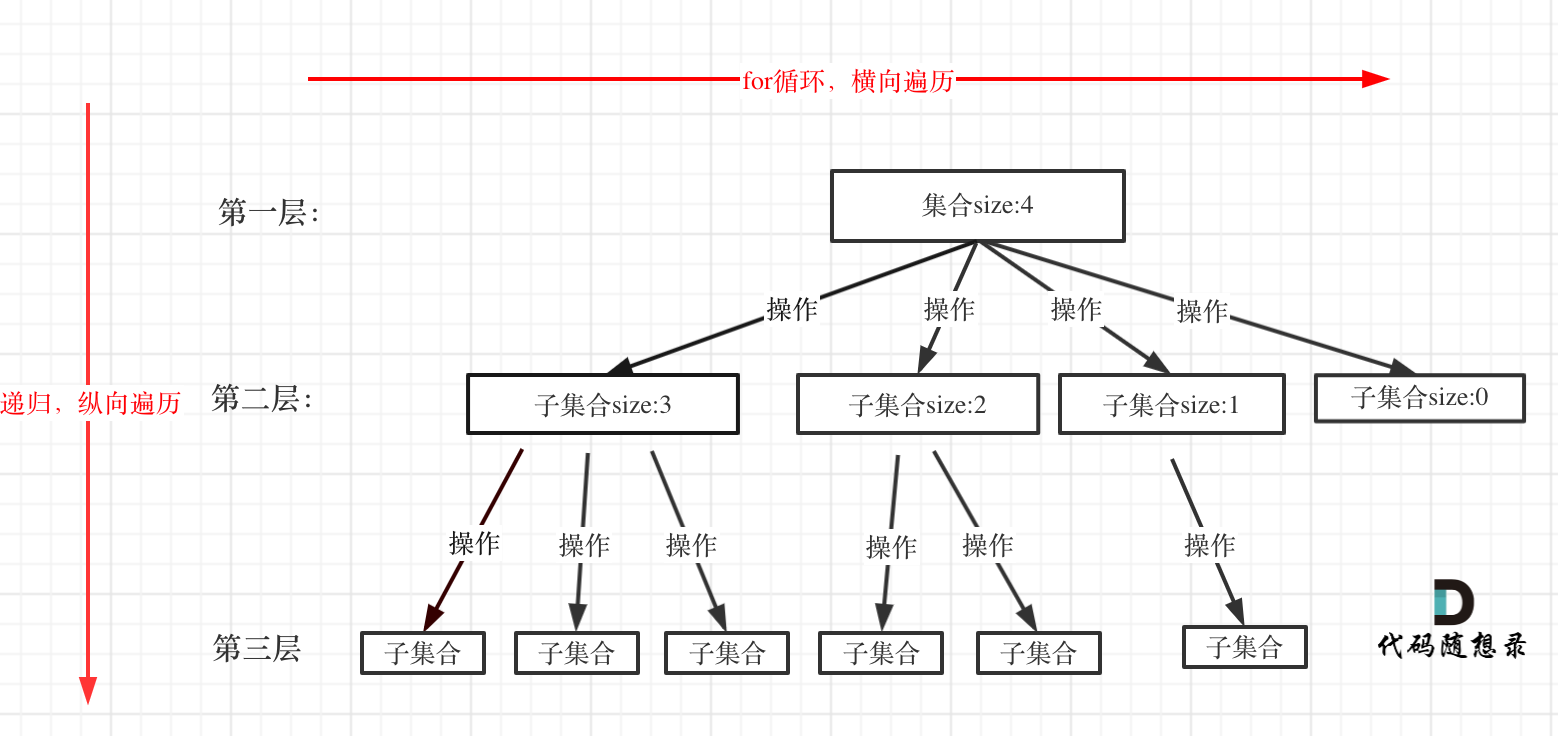
组合
n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
void backtrace(int n,int k,vector<int>& r,vector<vector<int>>& result,int startIndex) {
if(r.size() == k) {
result.push_back(r);
return;
}
for(int i = startIndex;i<=n;++i) {
r.push_back(i);
backtrace(n,k,r,result,i+1);
r.pop_back();
}
}
vector<vector<int>> combine(int n, int k) {
vector<vector<int>> result; // 路径
vector<int> r;
backtrace(n,k,r,result,1);
return result;
}
};组合总和III
n 的 k 个数的组合，且满足下列条件：1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
void backtrace(vector<vector<int>>& result, vector<int>& r, int n, int k,int startIndex,int sum) {
if(r.size() == k && sum == n) {
result.push_back(r);
return;
}
if(r.size()>=k) {
return;
}
for(int i =startIndex;i<=9;++i) {
r.push_back(i);
backtrace(result,r,n,k,i+1,sum+i);
r.pop_back();
}
}
vector<vector<int>> combinationSum3(int k, int n) {
vector<vector<int>> result;
vector<int> r; // 路径
backtrace(result,r,n,k,1,0);
return result;
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
public:
void backtrace(vector<vector<int>>& result, vector<int>& r, int n, int k,
int startIndex, int sum) {
if (r.size() == k) {
if (sum == n) {
result.push_back(r);
}
return;
}
if(sum>=n) {
return;
}
for (int i = startIndex; i <= 9-(k-r.size())+1; ++i) {
r.push_back(i);
backtrace(result, r, n, k, i + 1, sum + i);
r.pop_back();
}
}
vector<vector<int>> combinationSum3(int k, int n) {
vector<vector<int>> result;
vector<int> r; // 路径
backtrace(result, r, n, k, 1, 0);
return result;
}
};电话号码组合
2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40class Solution {
private:
public:
void backtrace(vector<string>& result,const unordered_map<char,string>& phoneMap,const string& digits,string& combination) {
if(combination.size() == digits.size()) {
result.push_back(combination);
}else{
// 根据index添加字符
auto digit = digits.at(combination.size());
auto s = phoneMap.at(digit);
for(auto ch:s) {
combination.push_back(ch);
backtrace(result,phoneMap,digits,combination);
combination.pop_back();
}
}
}
vector<string> letterCombinations(string digits) {
if(digits.empty()) {
return {};
}
unordered_map<char, string> phoneMap{
{'2', "abc"},
{'3', "def"},
{'4', "ghi"},
{'5', "jkl"},
{'6', "mno"},
{'7', "pqrs"},
{'8', "tuv"},
{'9', "wxyz"}
};
// 回溯法
string combination;
vector<string> result;
backtrace(result,phoneMap,digits,combination);
return result;
}
};组合总和
candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。target 的不同组合数少于 150 个。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36class Solution {
public:
void backtrace(vector<vector<int>>& result, vector<int>& r,
const vector<int>& candidates, int target, int sum,
int startIndex) {
if (target == sum) {
result.push_back(r);
} else {
// 选择
int rest = target - sum;
for (int i = 0; i < candidates.size(); ++i) {
int num = candidates.at(i);
if (num > rest) {
return;
} else {
if (i >= startIndex) {
r.push_back(num);
backtrace(result, r, candidates, target, sum + num,
i);
r.pop_back();
}
}
}
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
// 回溯 路径 选择 结束条件
// 重复 剪支
sort(candidates.begin(), candidates.end());
vector<vector<int>> result;
vector<int> r;
backtrace(result, r, candidates, target, 0, 0);
return result;
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
void backtrace(vector<int>& candidates, vector<vector<int>>& result,
vector<int>& r, int targetSum,int startIndex) {
if (targetSum == 0) {
result.push_back(r);
return;
}
if (targetSum < 0) {
return;
}
for (int i = startIndex; i < candidates.size(); ++i) {
if (targetSum < candidates[i]) {
break;
}
r.push_back(candidates[i]);
backtrace(candidates, result, r, targetSum - candidates[i],i);
r.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
// 回溯 路径 选择 结束条件
// 重复 剪支
sort(candidates.begin(), candidates.end());
vector<vector<int>> result;
vector<int> r;
backtrace(candidates,result,r,target,0);
return result;
}
};组合总和II
candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用 一次 。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38class Solution {
public:
void backtrace(vector<int>& candidates, int targetSum,vector<vector<int>> & result,vector<int>& path,int startIndex) {
if(targetSum == 0) {
result.push_back(path);
return;
}
// if(targetSum<0) {
// return;
// }
for(int i = startIndex;i<candidates.size();i++) {
if(targetSum<candidates[i]) {
break;
}
if(i>startIndex && candidates[i] == candidates[i-1]) {
continue;
}
// if(!path.empty() &&path.back() == candidates[i]) {
// //重复
// continue;
// }
path.push_back(candidates[i]);
backtrace(candidates,targetSum-candidates[i],result,path,i+1);
path.pop_back();
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
sort(candidates.begin(),candidates.end());
vector<vector<int>> result;
vector<int> path;
backtrace(candidates,target,result,path,0);
return result;
}
};分割回文串
s，请你将 s 分割成一些 子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39class Solution {
public:
bool isParo(const string& s) {
int i = 0, j = s.size() - 1;
while (i < j) {
if (s[i] != s[j]) {
return false;
}
i++;
j--;
}
return true;
}
void backtrace(const string& s, vector<vector<string>>& result,
vector<string>& path, int startIndex) {
if (startIndex == s.size()) {
result.push_back(path);
return;
}
for (int i = startIndex; i < s.size(); ++i) {
string tmp = s.substr(startIndex, i-startIndex + 1);
if (isParo(tmp)) {
// 回文串,进行回溯
path.push_back(tmp);
backtrace(s,result,path,i+1);
path.pop_back();
}else{
// 不是回文串 这个位置跳过
continue;
}
}
}
vector<vector<string>> partition(string s) {
vector<vector<string>> result;
vector<string> path;
backtrace(s,result,path,0);
return result;
}
};for (int i = startIndex; i < s.size(); i++)循环中，我们 定义了起始位置startIndex，那么 [startIndex, i] 就是要截取的子串。vector<string> path中，path用来记录切割过的回文子串1
2
3
4
5
6
7
8
9
10
11
12void computePalindrome(const string& s) {
// isPalindrome[i][j] 代表 s[i:j](双边包括)是否是回文字串
isPalindrome.resize(s.size(), vector<bool>(s.size(), false)); // 根据字符串s, 刷新布尔矩阵的大小
for (int i = s.size() - 1; i >= 0; i--) {
// 需要倒序计算, 保证在i行时, i+1行已经计算好了
for (int j = i; j < s.size(); j++) {
if (j == i) {isPalindrome[i][j] = true;}
else if (j - i == 1) {isPalindrome[i][j] = (s[i] == s[j]);}
else {isPalindrome[i][j] = (s[i] == s[j] && isPalindrome[i+1][j-1]);}
}
}
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56class Solution {
public:
bool isParo(const string& s) {
int i = 0, j = s.size() - 1;
while (i < j) {
if (s[i] != s[j]) {
return false;
}
i++;
j--;
}
return true;
}
void backtrace(const string& s, vector<vector<string>>& result,
vector<string>& path, int startIndex,const vector<vector<bool>>& dp) {
if (startIndex == s.size()) {
// 达到最后切割位置
result.push_back(path);
return;
}
for(int i = startIndex;i<s.size();++i) {
// string tmp = s.substr(startIndex,i-startIndex+1);
if(dp[startIndex][i]) {
path.push_back(s.substr(startIndex,i-startIndex+1));
backtrace(s,result,path,i+1,dp);
path.pop_back();
}else{
continue; // 扩大范围
}
}
}
vector<vector<bool>> computePalin(const string&s) {
int sz = s.size();
vector<vector<bool>> dp(sz,vector<bool>(sz));
// dp[i][j] 表示[i,j]字符串是否是回文
for(int i = sz-1;i>=0;i--) {
for(int j = i;j<sz;j++) {
if(i == j) {
dp[i][j] = true;
}else if(i == j-1 && s[i] == s[j]) {
dp[i][j] = true;
}else{
dp[i][j] = (s[i] == s[j]) && dp[i+1][j-1];
}
}
}
return dp;
}
vector<vector<string>> partition(string s) {
vector<vector<string>> result;
vector<string> path;
auto dp = computePalin(s);
backtrace(s, result, path, 0,dp);
return result;
}
};复原IP地址
for (int i = startIndex; i < s.size(); i++)循环中 [startIndex, i] 这个区间就是截取的子串，需要判断这个子串是否合法。如果合法就在字符串后面加上符号.表示已经分割。.），同时记录分割符的数量pointNum 要 +1。回溯的时候，就将刚刚加入的分隔符. 删掉就可以了，pointNum也要-1。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57class Solution {
public:
bool isValidIp(const string& s,int startIndex,int endIndex) {
// 不能超过255
// 每个字符有效 0-9
// 长度大于1不以0开头
if(startIndex>endIndex) {
return false;
}
if (s[startIndex] == '0' && startIndex!=endIndex) {
return false;
}
long long n{};
for (int i = startIndex; i <= endIndex; ++i) {
if (s[i] < '0' && s[i] > '9') {
return false;
}
n = n * 10 + (s[i] - '0');
if (n > 255) {
return false;
}
}
return true;
}
// startIndex是分割开始位置,dotNum是已经分段的数量
void backtrace( string& s, vector<string>& result, int startIndex,
int dotNum) {
if (dotNum == 3) {
// 点号数量到达3,ip地址固定
// 检测最后一段是否合法
// string tmp = s.substr(startIndex);
if (isValidIp(s,startIndex,s.size()-1)) {
result.push_back(s);
}
return;
}
for (int i = startIndex; i < s.size(); ++i) {
// string tmp = s.substr(startIndex, i - startIndex + 1);
if (isValidIp(s,startIndex,i)) {
// 在末尾添加.
s.insert(s.begin()+i+1,'.'); // 插入句号
backtrace(s, result, i + 2, dotNum + 1);
s.erase(s.begin()+i+1);
} else {
break;
}
}
}
vector<string> restoreIpAddresses(string s) {
if(s.size()<4 || s.size()>12) {
return {};
}
vector<string> result;
backtrace(s, result, 0, 0);
return result;
}
};子集
nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
void backtrace(vector<int>&nums,vector<vector<int>>& result,vector<int>& path,int startIndex) {
result.push_back(path);
if(startIndex == nums.size()) {
return;
}
for(int i = startIndex;i<nums.size();++i) {
path.push_back(nums[i]);
backtrace(nums,result,path,i+1);
path.pop_back();
}
}
vector<vector<int>> subsets(vector<int>& nums) {
vector<vector<int>> result;
vector<int> path;
backtrace(nums,result,path,0);
return result;
}
};子集II
nums ，其中可能包含重复元素，请你返回该数组所有可能的 子集（幂集）。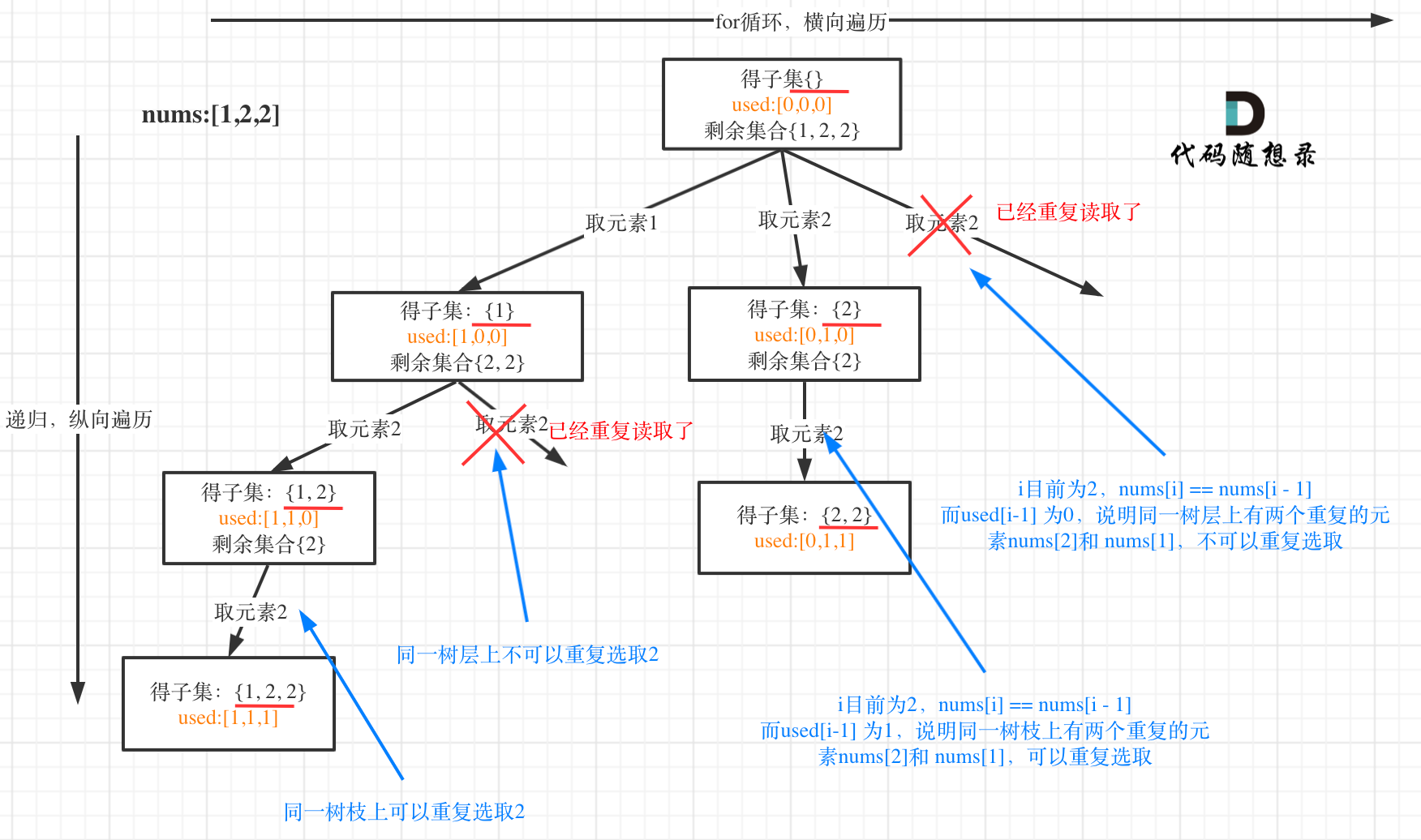
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
void backtrace(vector<int>& nums,vector<vector<int>>& result,vector<int>& path,int startIndex) {
result.push_back(path);
if(startIndex == nums.size()) {
return;
}
for(int i = startIndex;i<nums.size();++i) {
if(i>startIndex && nums[i] == nums[i-1]) {
continue;
}
path.push_back(nums[i]);
backtrace(nums,result,path,i+1);
path.pop_back();
}
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
vector<vector<int>> result;
vector<int> path;
sort(nums.begin(),nums.end());
backtrace(nums,result,path,0);
return result;
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
result.push_back(path);
for (int i = startIndex; i < nums.size(); i++) {
// used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
// used[i - 1] == false，说明同一树层candidates[i - 1]使用过
// 而我们要对同一树层使用过的元素进行跳过
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}
path.push_back(nums[i]);
used[i] = true;
backtracking(nums, i + 1, used);
used[i] = false;
path.pop_back();
}
}
public:
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
result.clear();
path.clear();
vector<bool> used(nums.size(), false);
sort(nums.begin(), nums.end()); // 去重需要排序
backtracking(nums, 0, used);
return result;
}
}递增子序列
nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。unordered_set<int> uset; 是记录本层元素是否重复使用，新的一层uset都会重新定义1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29class Solution {
public:
void backtrace(vector<int>& nums, vector<vector<int>>& result,
vector<int>& path, int startIndex) {
if (path.size() >= 2) {
result.push_back(path);
}
if (startIndex == nums.size()) {
return;
}
unordered_set<int> uset;
array<bool,201> arr{false};
for (int i = startIndex; i < nums.size(); ++i) {
if ((path.empty() || nums[i] >= path.back()) && arr[nums[i]+100] == false) {
path.push_back(nums[i]);
// uset.insert(nums[i]);
arr[nums[i]+100] = true;
backtrace(nums, result, path, i + 1);
path.pop_back();
}
}
}
vector<vector<int>> findSubsequences(vector<int>& nums) {
vector<vector<int>> result;
vector<int> path;
backtrace(nums, result, path, 0);
return result;
}
};全排列
nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
public:
void backtrace(vector<int>& nums,vector<vector<int>>& result,vector<int>& path,vector<bool>& used) {
if(path.size() == nums.size()) {
result.push_back(path);
return;
}
for(int i = 0;i<nums.size();++i) {
if(used[i]) {
continue;
}
path.push_back(nums[i]);
used[i] = true;
backtrace(nums,result,path,used);
used[i] = false;
path.pop_back();
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> result;
vector<int> path;
vector<bool> used(nums.size());
backtrace(nums,result,path,used);
return result;
}
};全排列II
nums ，按任意顺序 返回所有不重复的全排列。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution {
public:
void backtrace(vector<int>& nums, vector<vector<int>>& result,
vector<int>& path, vector<bool>& used) {
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
array<bool, 21> arr{false};
// unordered_set<int> umap;
for (int i = 0; i < nums.size(); ++i) {
if (used[i] || arr[nums[i]+10]) {
continue;
}
arr[nums[i]+10] = true;
path.push_back(nums[i]);
used[i] = true;
backtrace(nums, result, path, used);
used[i] = false;
path.pop_back();
}
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
vector<int> path;
vector<vector<int>> result;
vector<bool> used(nums.size());
backtrace(nums, result, path, used);
return result;
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking (vector<int>& nums, vector<bool>& used) {
// 此时说明找到了一组
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
for (int i = 0; i < nums.size(); i++) {
// used[i - 1] == true，说明同一树枝nums[i - 1]使用过
// used[i - 1] == false，说明同一树层nums[i - 1]使用过
// 如果同一树层nums[i - 1]使用过则直接跳过
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}
if (used[i] == false) {
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
}
public:
vector<vector<int>> permuteUnique(vector<int>& nums) {
result.clear();
path.clear();
sort(nums.begin(), nums.end()); // 排序
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return result;
}
};重新安排行程
tickets ，其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小，排序更靠前。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37class Solution {
public:
bool backtrace(unordered_map<string, map<string, int>>& tours,int tsz,vector<string>& result) {
// 截止条件
if(result.size()-1 == tsz) {
return true;
}
// 选择
string startpos = result.back();
for(auto& t:tours[startpos]) {
if(t.second>0) {
// 能到达
t.second--;
result.push_back(t.first);
if(backtrace(tours,tsz,result)) {
return true;
}
result.pop_back();
t.second++;
}
}
return false;
}
vector<string> findItinerary(vector<vector<string>>& tickets) {
// 使用什么数据结构存储
unordered_map<string, map<string, int>> tours;
for (auto ticket : tickets) {
tours[ticket[0]]
[ticket[1]]++; // 使用 map作为键,保证顺序,并记录行程避免死循环
}
vector<string> result;
int tsz = tickets.size(); // 票的数目 用于截止条件
result.push_back("JFK");
backtrace(tours,tsz,result);
return result;
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
private:
// unordered_map<出发机场, map<到达机场, 航班次数>> targets
unordered_map<string, multiset<string>> targets;
public:
vector<string> findItinerary(vector<vector<string>>& tickets) {
vector<string> result;
for (const vector<string>& vec : tickets) {
targets[vec[0]].insert(vec[1]); // 记录映射关系
}
stack<string> s;
s.push("JFK");
while (!s.empty()) {
auto t = s.top();
if (targets[t].empty()) {
// 到达最后位置
result.push_back(t);
s.pop();
} else {
s.push(*targets[t].begin()); // 加入栈中
targets[t].erase(targets[t].begin()); // 删除这条边
}
}
reverse(result.begin(), result.end());
return result;
}
};N皇后
n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。n ，返回所有不同的 n 皇后问题 的解决方案。'Q' 和 '.' 分别代表了皇后和空位1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45class Solution {
public:
bool isValid(vector<string>& board, int row, int col, int n) {
for (int i = 0; i < row; ++i) {
if (board[i][col] == 'Q') {
// 同一列不能出现
return false;
}
}
// 检查斜线
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; j--, i--) {
if (board[i][j] == 'Q') {
return false;
}
}
for (int i = row - 1, j = col + 1; j < n && i >= 0; j++, i--) {
if (board[i][j] == 'Q') {
return false;
}
}
return true;
}
void backtrace(vector<string>& path, vector<vector<string>>& result, int n,
int row) {
if (row == n) {
result.push_back(path);
return;
}
for (int i = 0; i < n; ++i) {
if (isValid(path, row, i, n)) {
path[row][i] = 'Q';
backtrace(path, result, n, row + 1);
path[row][i] = '.';
}
}
}
vector<vector<string>> solveNQueens(int n) {
vector<string> path(n,string(n,'.'));
vector<vector<string>> result;
backtrace(path,result,n,0);
return result;
}
};
解数独
1-9 在每一行只能出现一次。1-9 在每一列只能出现一次。1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）'.' 表示1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48class Solution {
public:
bool isValid(vector<vector<char>>& board, int i, int j, char k) {
int r = board.size();
int c = board[0].size();
for (int t = 0; t < c; t++) {
if (board[i][t] == k) {
return false;
} // 检查行
}
for (int t = 0; t < r; t++) {
if (board[t][j] == k) {
return false;
} // 检查列
}
i = (i / 3) * 3;
j = (j / 3) * 3;
for (int m = i; m < i + 3; m++) {
for (int n = j; n < j + 3; n++) {
if (board[m][n] == k) {
return false;
}
} // 检查3x3单元格内不重复
}
return true;
}
bool backtrace(vector<vector<char>>& board) {
int row = board.size();
int col = board[0].size();
for (int i = 0; i < row; ++i) {
for (int j = 0; j < col; ++j) {
if (board[i][j] == '.') {
for (char k = '1'; k <= '9'; k++) {
if (isValid(board,i, j, k)) {
board[i][j] = k;
if(backtrace(board))
return true;
board[i][j] = '.';
}
}
return false;
}
}
}
return true;
}
void solveSudoku(vector<vector<char>>& board) { backtrace(board); }
};搜索与排序
排序
快速排序
arr[low...high] 以 pivot 为基准进行分区。arr[high] 作为基准（或其他位置，然后交换到 high）。i，指向“小于基准”区域的最后一个元素。j 从 low 到 high-1：arr[j] <= pivot，则将 arr[j] 交换到 arr[i+1] 的位置，并增加 i。arr[high]）交换到 arr[i+1] 的位置。i+1，即基准最终的索引。arr[low] 作为基准（或其他位置）。i（从 low-1 开始向右移动）和 j（从 high+1 开始向左移动）。while (true) 循环：do i++ 直到 arr[i] >= pivot。do j-- 直到 arr[j] <= pivot。i < j，交换 arr[i] 和 arr[j]。j（或 i，取决于实现）。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29void quickSort( vector<int>& nums,int l,int r) {
if(l>=r) {
return;
}
int pivotIndex = partition(nums,l,r);
// quickSort(nums,l,pivotIndex-1);
quickSort(nums,l,pivotIndex-1);
quickSort(nums,pivotIndex+1,r);
}
int partition(vector<int>& nums,int l , int r) {
int pivotIndex = l;
int pivot = nums.at(pivotIndex);
if(l>=r) {
return l;
}
// hore分区
while(l<r) {
while(l<r && nums.at(l)<=pivot) {
l++;
}
while(l<r && nums.at(r)>=pivot) {
r--;
}
swap(nums.at(l),nums.at(r));
}
l = nums.at(l)>pivot?l-1:l;
swap(nums.at(pivotIndex),nums.at(l));
return l;
}归并排序
前缀树
相关知识
true。true，则说明找到了该单词。考点
LeetCode 题目实践
Trie 类，包含 insert、search 和 startsWith 三个方法。通过这道题可以巩固对前缀树结构的理解。insert(word)：将单词 word 插入前缀树。search(word)：判断 word 是否在前缀树中。startsWith(prefix)：判断是否有以 prefix 为前缀的单词1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69class TrieNode {
public:
vector<TrieNode*> chars{26,nullptr};
bool isEndOfWord{};
};
class Trie {
public:
TrieNode* trieRoot;
public:
Trie():trieRoot(new TrieNode) {
}
void insert(string word) {
if(word.empty()) {
return;
}
auto node = trieRoot;
for(auto ch:word) {
auto n = node->chars[ch-'a'];
if(n == nullptr) {
n = new TrieNode;
node->chars[ch-'a'] = n;
}
node = n;
}
node->isEndOfWord = true;
}
bool search(string word) {
if(word.empty()) {
return false;
}
auto node = trieRoot;
for(auto ch:word) {
auto n = node->chars[ch-'a'];
if(n == nullptr) {
return false;
}
node = n;
}
return node->isEndOfWord;
}
bool startsWith(string prefix) {
if(prefix.empty()) {
return false;
}
auto node = trieRoot;
for(auto ch:prefix) {
auto n = node->chars[ch-'a'];
if(n == nullptr) {
return false;
}
node = n;
}
return true;
}
};
/**
* Your Trie object will be instantiated and called as such:
* Trie* obj = new Trie();
* obj->insert(word);
* bool param_2 = obj->search(word);
* bool param_3 = obj->startsWith(prefix);
*/insert(key, val)：在插入时，从根节点开始遍历 key 的每个字符。每经过一个节点，都将该节点的累加值更新为 val。sum(prefix)：遍历 prefix 对应的路径，返回最后一个节点的累加值。区间集合
其他
汉诺塔
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
int n = A.size();
move(n,A,B,C);
}
void move(int n,vector<int>& A,vector<int>&B,vector<int>& C) {
if(n == 1) {
C.push_back(A.back());
A.pop_back();
return;
}
move(n-1,A,C,B); // 将A上面的n-1个盘子移动到B,通过C
C.push_back(A.back()); // 将最下面的盘子放到C
A.pop_back(); // 弹出A 此时A没有盘子
move(n-1,B,A,C); // 将B上面的n-1个盘子移动到C,通过A
}
};c++刷题
vector的常用操作
std::vector 是 C++ STL 中最常用的容器之一，因为它兼具动态数组的灵活性和 C 风格数组的性能优势。但在 LeetCode 刷题或实际开发中，如果不注意一些细节，它也可能带来性能问题或难以排查的 bug。std::vector 常用方法注意事项1. 索引访问：
[] vs. .at()vec[index] (下标运算符)：index 超出 [0, vec.size() - 1] 范围，会导致未定义行为 (Undefined Behavior)。这可能表现为程序崩溃、数据损坏或看似随机的错误。vec.at(index) (成员函数)：index 超出范围，会抛出 std::out_of_range 异常，这使得调试更容易。[]。.at()。2.
push_back() 的性能与 reserve()vec.push_back(value)：vector 的当前容量不足以容纳新元素时，它会进行重新分配 (reallocation)。vector 很大时。频繁的重新分配会严重影响性能。vec.reserve(new_cap)：new_cap 大小的内存空间，但不改变 vector 的实际大小 (size())。vector 大致会增长到多大，或者需要添加大量元素，预先调用 reserve() 可以避免多次重新分配，显著提升性能。reserve() 只能增加容量，不能减少。3. 迭代器失效 (Iterator Invalidation)
vector 发生重新分配时：所有指向其内部元素的迭代器、指针和引用都会失效。这意味着它们可能指向错误的内存地址，或者指向已经被释放的内存。push_back() (当容量不足时)insert()resize()erase() (虽然 erase 返回下一个有效迭代器，但它也会使被删除元素及之后的所有迭代器失效)erase() 操作时，如果使用传统的 for 循环，必须小心处理返回的迭代器：it = vec.erase(it);erase 的重载版本都会使从被删除元素（或范围）开始到 vector 末尾的所有迭代器、指针和引用失效。因此，在使用 erase 后，你通常需要重新获取迭代器。 erase主要是删除指定迭代器或者迭代器范围,参数没有size_type指定索引的类型.std::remove 和 erase-remove 惯用法erase，而是使用 std::remove (或 std::remove_if) 结合 vector::erase 的惯用法。这种方法通常更高效，因为它只进行一次数据移动。std::remove (或 std::remove_if)：这是一个算法（在 <algorithm> 中），它将所有要“删除”的元素移动到范围的末尾，并返回一个指向新逻辑末尾的迭代器。它不实际删除元素，也不改变容器的大小。vector::erase：然后使用 vector::erase 来删除从 std::remove 返回的迭代器到 vector.end() 之间的元素，从而真正改变 vector 的大小并释放内存。4.
pop_back() 与 front()/back() 的使用vec.pop_back() 和 vec.front() / vec.back()：vector 非空（即 !vec.empty()）。如果 vector 为空时调用它们，会导致未定义行为。vec.front()vector 中第一个元素的引用。T&)。vector 不能为空。调用空 vector 的 front() 会导致未定义行为。int first = myVector.front();vec.back()vector 中最后一个元素的引用。T&)。vector 不能为空。调用空 vector 的 back() 会导致未定义行为。int last = myVector.back();vec.data() (C++11)vector 内部存储数据的首个元素的指针。这允许你将 vector 的数据作为 C 风格数组传递给 C 语言 API。T* (非 const 版本) 或 const T* ( const 版本)。vector 重新分配内存后会失效。int* rawArray = myVector.data();5.
clear() vs. shrink_to_fit()vec.clear():vector 中的所有元素，使其 size() 变为 0。vector 内部已分配的内存，capacity() 可能保持不变。vec.shrink_to_fit() (C++11):vector 将其容量调整到刚好足以容纳当前元素（即 capacity() 变为 size()）。这是一个提示，不保证一定会减少容量。vector 之前有过大量元素，然后清空或删除了大部分，但你希望立即释放多余内存以节省资源，可以使用它。但频繁调用也可能导致不必要的开销。6.插入与删除元素
vec.insert(const_iterator position, const T& value) / vec.insert(const_iterator position, T&& value)position 迭代器指向的位置之前插入一个 value。position 及其之后所有迭代器失效。如果容量不足，会触发重新分配。时间复杂度为 O(N)，因为需要移动 position 之后的所有元素。auto it = myVector.insert(myVector.begin() + 1, 99);ec.insert(const_iterator position, size_type count, const T& value)position 迭代器指向的位置之前插入 count 个 value。insert。vec.insert(const_iterator position, InputIt first, InputIt last)position 迭代器指向的位置之前插入 [first, last) 范围内的元素。insert。vec.emplace(const_iterator position, Args&&... args) (C++11)position 迭代器指向的位置就地构造一个元素。insert。vec.erase(const_iterator position)position 迭代器指向的单个元素。vec.end()。position 及其之后的所有迭代器失效。时间复杂度为 O(N)。auto it_next = myVector.erase(myVector.begin() + 1);vec.erase(const_iterator first, const_iterator last)[first, last) 范围内的元素。vector 的所有元素直到末尾，则返回 vec.end()。first 及其之后的所有迭代器失效。时间复杂度为 O(N)。auto it_next = myVector.erase(myVector.begin() + 1, myVector.begin() + 3);vec.swap(std::vector& other)vector 的内容。这是一种常数时间操作，因为它只交换了内部的指针和大小信息。void。vector 对象了。7.构造函数与
resize() 的区别std::vector<T> vec(count);：创建 count 个元素，并对它们进行默认初始化。vec.resize(count);：如果 count 大于当前 size()，会添加新的元素并进行默认初始化。vec.clear(); 之后再 vec.resize(count);：会清空现有元素，然后创建 count 个新元素并默认初始化。string的常用操作
std::string& insert(size_type index, const std::string& str); 等重载*this）。index 插入内容。index 不能超过 size()，否则抛出 std::out_of_range。插入操作可能涉及大量字符移动，性能开销较大。std::string& erase(size_type index = 0, size_type count = npos); 等重载*this）。index 位置开始删除 count 个字符。index 不能超过 size()，否则抛出 std::out_of_range。删除操作可能涉及大量字符移动。std::string substr(size_type pos = 0, size_type len = npos) const;pos 位置开始，长度为 len 的新字符串。pos 不能超过 size()，否则抛出 std::out_of_range。len 超过实际可用长度时会被截断。1
2
3
4
5
6
7iterator erase(const_iterator position);
iterator erase(const_iterator first, const_iterator last);
iterator insert(const_iterator pos, CharT c);
iterator insert(const_iterator pos, size_type count, CharT c);
template<class InputIt>
iterator insert(const_iterator pos, InputIt first, InputIt last);insert 操作都可能导致字符串重新分配内存，这会使所有之前获得的指向该字符串内部的迭代器和指针失效。这意味着你不能在 insert 操作之后依赖旧的迭代器继续操作。如果你需要继续迭代，应该使用 insert 的返回值（新的迭代器）。size_type find(const std::string& str, size_type pos = 0) const; / find(CharT c, size_type pos = 0) const; 等重载std::string::npos。pos 指定从哪个位置开始查找。npos 是 size_type 的一个特殊静态成员常量，通常是 size_type 的最大值，表示“找不到”。size_type rfind(const std::string& str, size_type pos = npos) const; 等重载std::string::npos。rfind 从字符串末尾开始向前查找（但返回的索引是从字符串开头算的）。size_type find_first_of(const std::string& str, size_type pos = 0) const; 等重载str 中任意一个字符在当前字符串中第一次出现的索引。str 是 "aeiou"，它会查找 a 或 e 或 i 或 o 或 u 中任意一个字符的第一次出现。size_type find_last_of(const std::string& str, size_type pos = npos) const; 等重载str 中任意一个字符在当前字符串中最后一次出现的索引。size_type find_first_not_of(const std::string& str, size_type pos = 0) const; 等重载str 中的字符在当前字符串中第一次出现的索引。size_type find_last_not_of(const std::string& str, size_type pos = npos) const; 等重载str 中的字符在当前字符串中最后一次出现的索引。std::string& replace(size_type pos, size_type len, const std::string& str); 等重载*this）。pos 位置开始、长度为 len 的子串替换为 str。std::string 会自动管理内存，你无需手动 new 或 delete。当字符串内容变化且当前容量不足时，它会自动重新分配内存（通常会以指数级增长，如 1.5 倍或 2 倍）。std::string 的大多数操作都提供异常安全保证。reserve() 预分配内存，或者考虑使用其他数据结构（如 std::vector<char> 或字符数组）在底层操作，再转换为 std::string。std::string::npos： 这是一个静态成员常量，表示“未找到”或“到字符串末尾”。front()、back()、operator[] 或 erase() 等可能需要非空字符串的操作时，要特别注意空字符串的情况，避免未定义行为。list与deque的常用操作
std::list 是一个双向链表实现，这意味着它的元素在内存中不一定是连续存储的。每个元素都包含指向前一个和后一个元素的指针。[] 或 at() 直接访问元素，访问元素需要线性时间 O(n) 遍历。std::vector 和 std::deque 有更高的内存开销。iterator erase(const_iterator pos);pos 处元素。O(1) 复杂度。pos 必须有效且不能是 end()。iterator erase(const_iterator first, const_iterator last);[first, last) 的元素std::list 作为双向链表，其核心优势在于高效的非尾部插入和删除以及迭代器稳定性。因此，它拥有一系列专门针对链表特性的方法：splice() 系列方法std::list 最独特且功能强大的方法之一。它能以 O(1) 的复杂度（不包括查找插入位置和移动元素的迭代器）将一个 list 的元素移动到另一个 list 中，或者移动一个 list 中的部分元素。元素不是复制，而是直接修改它们的链表指针，效率极高。void splice(const_iterator pos, std::list& other);：将 other 整个列表的所有元素移动到当前列表的 pos 之前。other 列表会变空。void splice(const_iterator pos, std::list& other, const_iterator it);：将 other 列表中 it 指向的单个元素移动到当前列表的 pos 之前。void splice(const_iterator pos, std::list& other, const_iterator first, const_iterator last);：将 other 列表中 [first, last) 范围内的元素移动到当前列表的 pos 之前。vector 对比： std::vector 没有 splice 方法，因为其底层是连续内存，任何元素的“移动”实际上都是复制和删除，需要 O(n) 复杂度。remove() 和 remove_if()remove）或满足特定条件（remove_if）的元素。void remove(const T& value);template<class Predicate> void remove_if(Predicate pred);vector 对比： std::vector 通常通过“移除-擦除 (erase-remove idiom)”来实现类似功能：vec.erase(std::remove(vec.begin(), vec.end(), value), vec.end());。这在 std::vector 中是 O(n) 操作，并且会移动元素，而 std::list 的 remove 操作是真正的 O(n) 遍历和 O(1) 删除每个元素。unique()void unique();template<class BinaryPredicate> void unique(BinaryPredicate binary_pred);vector 对比： std::vector 使用 std::unique 算法（同样需要配合 erase），它也只删除连续重复的元素。但 list 的 unique 是成员函数，是针对链表优化的。merge()void merge(std::list& other);template<class Compare> void merge(std::list& other, Compare comp);vector 对比： std::vector 通常使用 std::merge 算法，它会创建一个新容器来存放合并结果，而不是直接在原地合并并清空源容器。list 的 merge 操作是基于链表指针的 O(n) 高效合并。sort()void sort();template<class Compare> void sort(Compare comp);vector 对比： std::vector 使用全局函数 std::sort，它要求随机访问迭代器。由于 std::list 不支持随机访问，它不能使用 std::sort，因此它提供了自己的成员 sort() 方法，通常是基于归并排序（merge sort）的变种，以适应链表结构。reverse()void reverse();vector 对比： std::vector 可以使用 std::reverse 算法。list 的 reverse 是成员函数，针对链表结构优化。std::deque (double-ended queue) 是一个双端队列容器，它支持在两端（头部和尾部）快速插入和删除元素。它在内部通常实现为分段的动态数组，这意味着其元素在内存中不一定是连续的，但可以通过一个“映射”结构来快速访问。std::deque 的设计目标是支持两端的高效插入/删除，同时保留随机访问的能力。虽然它的特殊方法不如 std::list 那么多，但其头部操作是其显著优势push_front(), pop_front(), push_back(), pop_back() 都是常数时间复杂度 O(1)。[] 和 at() 进行随机访问，平均是常数时间复杂度 O(1) (因为它通过映射表快速找到对应内存段)。std::vector 更灵活，因为它不要求连续内存，但可能比 std::vector 有略高的间接访问开销。iterator insert(const_iterator pos, const T& value); / insert(const_iterator pos, T&& value); 等重载pos 迭代器指向的位置之前插入元素。中部插入是 O(n) 复杂度。pos 可以是 end()。所有迭代器可能失效。iterator insert(const_iterator pos, size_type count, const T& value);template<class InputIt> iterator insert(const_iterator pos, InputIt first, InputIt last);iterator erase(const_iterator pos);pos 处元素。中部删除是 O(n) 复杂度。pos 必须有效且不能是 end()。所有迭代器可能失效。iterator erase(const_iterator first, const_iterator last);[first, last) 的元素。void clear();void。void resize(size_type count); / void resize(size_type count, const T& value);void。void swap(std::deque& other);void。push_front()void push_front(const T& value);void push_front(T&& value);vector 对比： std::vector 没有 push_front() 方法。在 vector 的头部插入元素需要将所有现有元素后移，复杂度为 O(n)，效率极低。deque 的 push_front() 是常数时间复杂度 O(1) (均摊)。pop_front()void pop_front();vector 对比： std::vector 没有 pop_front() 方法。在 vector 的头部删除元素同样需要将所有后续元素前移，复杂度为 O(n)。deque 的 pop_front() 是常数时间复杂度 O(1) (均摊)。std::vector 专注于连续内存和快速随机访问，以及尾部操作。它的优势在于缓存局部性好，适合作为动态数组。std::list 则专注于高效的任意位置插入和删除，其 splice()、remove()、merge() 和成员 sort() 等方法都是其链表特性的体现，是 vector 所不具备的。std::deque 则是介于两者之间，它提供了 vector 的大部分功能（包括随机访问），同时具备 list 在两端操作上的 O(1) 优势，即 push_front() 和 pop_front() 是其独有且高效的操作。stack与queue
std::stack 和 std::queue 是 C++ 标准库（STL）中两种非常重要的容器适配器（Container Adapters）。它们不是独立的底层数据结构，而是将现有的序列容器（如 std::deque、std::list 或 std::vector）封装起来，提供特定的访问接口，从而模拟栈（LIFO，后进先出）和队列（FIFO，先进先出）的行为。std::stack<T> s;std::deque<T>。std::stack<int> myStack;std::stack<T, Container> s(container_obj);Container 创建栈，并用一个现有容器对象初始化。std::list<int> myList = {1, 2, 3}; std::stack<int, std::list<int>> myStackFromList(myList);s.push(const T& value)myStack.push(10);s.pop()myStack.pop();s.top()T& (对栈顶元素的引用)。int topElement = myStack.top();std::queue<T> q;std::deque<T>。std::queue<std::string> myQueue;std::queue<T, Container> q(container_obj);Container 创建队列，并用一个现有容器对象初始化。std::vector<std::string> myVec = {"A", "B"}; std::queue<std::string, std::vector<std::string>> myQueueFromVec(myVec); （注意：vector 不支持 pop_front，所以不能作为 queue 的底层容器。这里写错，正确的应该是 std::list 或 std::deque）std::deque<std::string> myDeque = {"A", "B"}; std::queue<std::string, std::deque<std::string>> myQueueFromDeque(myDeque);q.push(const T& value)myQueue.push("Task 1");q.pop()myQueue.pop();q.front()T& (对队头元素的引用)。std::string currentTask = myQueue.front();q.back()T& (对队尾元素的引用)。std::string lastAddedTask = myQueue.back();map/unordered_map
std::map 是 C++ 标准库中的一个有序关联容器，它存储键值对 (key-value pairs)。它的主要特点是：std::map 中不允许有重复的键。std::map 中的所有元素都会根据它们的键自动进行升序排序。默认情况下，它使用键类型的 operator< 进行排序。std::map<Key, Value> m;map。std::map<std::string, int> wordCounts;std::map<Key, Value> m = {{k1, v1}, {k2, v2}};map。std::map<int, char> grades = {{1, 'A'}, {2, 'B'}};std::map<Key, Value> m(first, last);[first, last) 初始化 map，范围内的元素必须是键值对类型（如 std::pair<Key, Value>）。m.insert({key, value}) / m.insert(std::make_pair(key, value))key 已存在，则插入失败，map 不会被修改。std::pair<iterator, bool>。iterator 指向新插入的元素或已存在的具有相同键的元素。bool 为 true 表示成功插入新元素，false 表示元素已存在。m.emplace(Args&&... args) (C++11)map 中就地构造一个键值对。通常比 insert 接受 std::pair 更高效。insert。m.erase(const Key& key)map 中匹配 key 的键值对。size_type，表示被删除元素的数量（对于 map 而言，总是 0 或 1，因为键是唯一的）。m.erase(iterator pos)pos 迭代器指向的单个元素。m.end()。m.erase(iterator first, iterator last)[first, last) 范围内的元素。m.count(const Key& key)map 中匹配 key 的元素数量。size_type (对于 map 而言，总是 0 或 1)。m.find(const Key& key)map 中匹配 key 的元素。m.end() 迭代器。m.lower_bound(const Key& key)key 的元素的迭代器。iterator。m.upper_bound(const Key& key)key 的元素的迭代器。iteratorstd::unordered_map 是一种无序的关联容器，它通过哈希表（Hash Table）实现。它也存储键值对，但元素没有特定的排序，而是根据键的哈希值来组织。um.insert({key, value}) / um.insert(std::make_pair(key, value))key 已存在，则插入失败。std::pair<iterator, bool>。同 std::map。um.emplace(Args&&... args) (C++11)insert。um.erase(const Key& key)unordered_map 中匹配 key 的键值对。size_type，表示被删除元素的数量（对于 unordered_map 而言，总是 0 或 1，因为键是唯一的）。um.erase(iterator pos)pos 迭代器指向的单个元素。um.erase(iterator first, iterator last)[first, last) 范围内的元素。um.count(const Key& key)unordered_map 中匹配 key 的元素数量。size_type (总是 0 或 1)。um.find(const Key& key)unordered_map 中匹配 key 的元素。um.end() 迭代器。set/unordered_set
std::set 是一种有序的关联容器，它存储唯一的元素，并且所有元素都根据其值的严格弱序（strict weak ordering）\进行排序。其底层通常实现为*红黑树（Red-Black Tree）*。std::set<T> s;set。std::set<int> mySet;std::set<T> s = {e1, e2, ...};set。std::set<std::string> uniqueWords = {"apple", "banana", "apple"}; (实际只存储 “apple”, “banana”)std::set<T> s(first, last);[first, last) 初始化 set。s.insert(const T& value) / s.insert(T&& value)value 已存在，则插入失败，set 不会被修改。std::pair<iterator, bool>。iterator 指向新插入的元素或已存在的相同元素。bool 为 true 表示成功插入新元素，false 表示元素已存在。s.emplace(Args&&... args) (C++11)set 中就地构造一个元素。insert。s.erase(const T& value)set 中匹配 value 的元素。size_type，表示被删除元素的数量（对于 set 而言，总是 0 或 1，因为元素是唯一的）。s.erase(iterator pos)pos 迭代器指向的单个元素。s.end()。s.erase(iterator first, iterator last)[first, last) 范围内的元素。s.count(const T& value)set 中匹配 value 的元素数量。size_type (对于 set 而言，总是 0 或 1)。s.find(const T& value)set 中匹配 value 的元素。s.end() 迭代器。s.lower_bound(const T& value)value 的元素的迭代器。iterator。s.upper_bound(const T& value)value 的元素的迭代器。iterator。std::set 的元素类型 (T) 必须是可比较的。这意味着它必须能够通过 operator< 进行排序，或者你需要提供一个自定义的比较函数。std::unordered_set 是一种无序的关联容器，它存储唯一的元素。其底层通过哈希表（Hash Table）实现。us.insert(const T& value) / us.insert(T&& value)value 已存在，则插入失败。std::pair<iterator, bool>。同 std::set。us.emplace(Args&&... args) (C++11)insert。us.erase(const T& value)unordered_set 中匹配 value 的元素。size_type，表示被删除元素的数量（对于 unordered_set 而言，总是 0 或 1）。us.erase(iterator pos)pos 迭代器指向的单个元素。us.erase(iterator first, iterator last)[first, last) 范围内的元素。us.count(const T& value)unordered_set 中匹配 value 的元素数量。size_type (总是 0 或 1)。us.find(const T& value)unordered_set 中匹配 value 的元素。us.end() 迭代器。erase与find的参数与对应返回值
priority_queue
std::priority_queue 是 C++ 标准库 (STL) 中的一个容器适配器 (Container Adapter)，它提供了一个类似队列的接口，但其内部元素总是按照特定优先级排序。默认情况下，它是一个最大堆（Max-Heap），意味着队头元素总是当前所有元素中最大的std::priority_queue<T> pq;std::vector<T>，默认比较器是 std::less<T> (用于实现最大堆)。std::priority_queue<int> max_heap;std::priority_queue<T, Container, Compare> pq(comp);Container 和自定义比较器 Compare 创建优先级队列。comp 是比较器的实例。1
std::priority_queue<int, std::vector<int>, std::greater<int>> min_heap;
std::greater<int> 使得“大”的元素优先级“低”（因为 a > b 为 true，a 就排在 b 后面），从而实现最小堆。pq.push(const T& value)max_heap.push(10);pq.pop()max_heap.pop();pq.top()const T& (对堆顶元素的常量引用)。int highest_priority_element = max_heap.top();pq.empty()bool (true 表示空，false 表示非空)。if (max_heap.empty()) { /* 队列为空 */ }pq.size()size_type (无符号整数类型)。std::cout << max_heap.size();vector 可以作为 map 的键但不能直接作为 unordered_map 的键std::map 是一个有序关联容器，它的底层通常实现为红黑树（一种自平衡二叉搜索树）。std::map 存储元素时，需要能够对键进行排序。这意味着 std::map 的键类型必须是可比较的 (Comparable)，具体来说，它需要支持小于运算符 operator<。std::vector 恰好默认提供了 operator< 的重载。的operator<` 是如何工作的？std::vector 的 operator< 执行的是字典序 (lexicographical comparison) 比较。这意味着它会逐个元素地比较两个 vector：vector 在某个位置上的元素不相等，那么拥有较小元素的那个 vector 被认为是“更小”的。vector 是另一个 vector 的前缀（即较短的那个 vector 的所有元素都与较长的 vector 的对应前缀元素相同），那么较短的那个 vector 被认为是“更小”的。std::map (基于红黑树)：operator<）。std::vector 默认提供了字典序的 operator<，所以它满足这个要求。std::unordered_map (基于哈希表)：std::hash 特化）和可相等比较的（通过 operator==）。std::vector 默认没有提供 std::hash 特化，所以它不满足这个要求，除非你自定义哈希函数。std::unordered_set 是一种无序集合容器，它存储唯一元素的集合。它的底层也是基于哈希表实现的。因此，它对所存储的元素类型有同样的要求：std::hash<T> 的特化，能够为元素类型 T 计算哈希值。T 必须支持 operator==，用于在哈希冲突时判断元素是否真正相等。std::map 的 key 是 std::vector，然后你对这个 作为 key 的 std::vector 对象本身 进行了修改（比如 push_back 元素或 clear），那会发生非常严重的问题，通常会导致未定义行为std::map 依靠键的顺序来组织其内部的红黑树结构。当你插入一个 std::vector 作为键时，map 会使用 std::vector 的 operator< 来确定这个键在树中的位置。vector 键（例如 push_back），它的内容就变了，这意味着它的字典序比较结果也可能改变。其他一些类
tuple
std::tuple 是一个固定大小的异构（heterogeneous）容器，可以存储不同类型的固定数量的对象。你可以把它想象成一个“增强版”的 std::pair，因为 pair 只能存储两个不同类型的元素，而 tuple 可以存储任意数量的不同类型元素。tuple 的大小在编译时就确定了，不能动态改变。tuple 的性能可以媲美直接使用多个独立变量，编译器可以进行很好的优化。1
2
3
4
5
6
7
8
9
10
11
12
13
14
std::tuple<int, double, std::string> t1(10, 3.14, "hello");
// 或使用 C++11 后的列表初始化（需要显式指定类型）
std::tuple<int, double, std::string> t2 = {20, 2.71, "world"};
auto t3 = std::make_tuple(30, 1.618, "C++"); // t3 类型为 std::tuple<int, double, const char*>
int i = std::get<0>(t1); // 获取第一个元素 (10)
double d = std::get<1>(t1); // 获取第二个元素 (3.14)
std::string s = std::get<2>(t1); // 获取第三个元素 ("hello")
constexpr size_t size = std::tuple_size<decltype(t1)>::value; // size = 3
auto person = std::make_tuple("Alice", 30, "New York");
auto [name, age, city] = person; // 相当于声明了 name, age, city 三个变量并赋值
std::cout << name << ", " << age << ", " << city << std::endl;array
std::array 是一个固定大小的同构序列容器，它封装了 C 风格的静态数组。它提供了像 std::vector 一样的 STL 容器接口（如迭代器、size()、at() 等），但它的大小在编译时就确定，且不能改变。它的数据是直接存储在栈上（如果大小允许且不是全局/静态），而不是堆上，避免了动态内存分配的开销。at()) 和易用性。1
2
3
4
std::array<int, 5> arr1; // 声明一个包含 5 个 int 的 array，元素默认初始化 (int 为 0)
std::array<double, 3> arr2 = {1.1, 2.2, 3.3}; // 使用初始化列表std下STL方法
遇到的错误
ptr + offset 操作，而 offset 是一个非常大的无符号数，或者实际上应该是一个负数但被误用为无符号数。1
2
3char* p = some_array + size; // p 指向数组末尾之后一个位置
unsigned int offset = some_large_unsigned_value;
char* invalid_p = p + offset; // 此时如果 offset 足够大，可能会导致地址回绕1
2
3char* p = some_array;
size_t invalid_idx = -1; // 这是一个非常大的无符号数
char element = p[invalid_idx]; // 等同于 p + invalid_idx，可能溢出u_var，并且执行 u_var - another_unsigned_var，如果 u_var < another_unsigned_var，结果将是一个非常大的正数（无符号数下溢）。1
2
3
4
5std::vector<int> v = {1, 2, 3};
size_t index = 0;
// 假设某种逻辑错误导致 index 变成了 0，然后你尝试 index - 1
size_t prev_index = index - 1; // prev_index 会变成 size_t 的最大值
int val = v[prev_index]; // 访问越界，很可能导致地址回绕size_t 或 unsigned int 作为索引或偏移量时，如果计算结果错误地变成了非常大的正数，就可能导致这种所谓的“溢出”。runtime error: reference binding to null pointer of type 'int' (stl_vector.h) 错误，是一个非常经典的 C++ 未定义行为 (Undefined Behavior, UB) 错误，而且它通常是由 AddressSanitizer (ASan) 或其他内存安全工具在运行时检测到的。错误信息清晰地指出：你正在尝试将一个引用绑定到一个空指针上，而这是 C++ 标准不允许的。stl_vector.h，但这通常意味着你的代码在尝试访问 std::vector 的某个元素时，使用了无效的索引，导致 std::vector 内部的指针（指向其元素存储的内存）被非法地用于引用绑定。错误的根本原因
[] 运算符或 at() 方法访问一个 std::vector 中不存在的元素。std::vector 为空或者你提供的索引超出了其有效范围时，会发生以下情况：std::vector 为空：std::vector 的 size() 为 0 时，它可能不分配任何内存，或者其内部的 data() 指针就是 nullptr。myVector[0]，编译器并不知道 myVector 是空的，它会直接计算 data() + 0，如果 data() 是 nullptr，结果仍然是 nullptr。*nullptr 进行解引用并尝试将其绑定到引用时，就会触发这个错误。i 大于或等于 myVector.size()。myVector[i] 的操作在内部通常被转换为 *(myVector.data() + i)。如果 i 足够大，超出了已分配内存的范围，甚至可能导致指针算术溢出（回到内存地址空间低端，接近 nullptr）或者直接尝试访问未映射的内存区域。myVector.data() + i 的结果接近或就是 nullptr，就会触发这个特定的错误相关资料
