现在入门可能都晚了
机器学习历史
1956 年提出 AI 概念,短短3年后(1959)Arthur Samuel就提出了机器学习的概念.
机器学习研究和构建的是一种特殊算法(而非某一个特定的算法),能够让计算机自己在数据中学习从而进行预测。
所以,机器学习不是某种具体的算法,而是很多算法的统称。
此外还有一个经典概念.
假设用 P 来评估计算机程序在某任务类 T 上的性能,若一个程序利用经验 E 在任务 T 上获得了性能改善,则我们就说关于 T 和 P, 该程序对 E 进行了学习。
机器学习中一些流行的任务 T 包括:
- 分类:基于特征将实例分为某一类。
- 回归:基于实例的其他特征预测该实例的数值型目标特征。
- 聚类:基于实例的特征实现实例的分组,从而让组内成员比组间成员更为相似。
- 异常检测:寻找与其他样本或组内实例有很大区别的实例。
- 其他更多任务
经验 E 指的是数据(没有数据我们什么也干不了)。根据训练方式,机器学习算法可以分为监督(supervised)和无监督(unsupervised)两类。无监督学习需要训练含有很多特征的数据集,然后学习出这个数据集上有用的结构性质。而监督学习的数据集除了含有很多特征外,它的每个样本都要有一个标签(label)或目标(target)
机器学习包含了很多种不同的算法,深度学习就是其中之一,其他方法包括决策树,聚类,贝叶斯等。
需要的知识:学会Numpy,matplotlib,seaborn,pandas和scipy.基本的一些方法要知道同时要知道如何查阅文档,这个可能更重要.
同时需要一些基础的数学知识.
监督学习:regression和classification.
无监督学习:clustering和密度估计.
一般步骤
收集数据
利用爬虫或是已有数据得到一般的未处理的文本文件等 格式可以为json,csv,xml或者一般的txt.
准备数据
使用python解析文本文件,一般利用简单的open读取,pandas等能够对所有数据进行解析.
目的得到数据的特征值和目标向量.
分析数据
使用matplotlib等可视化数据进行初步分析(通常需要得到二维扩散图)训练算法
后面会提到测试算法
使用测试数据作为测试样本,通过这一步得到算法的正确率使用算法
输入数据判断
Classification
进行分类 标称值
KNN
第一个分类器1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24import operator
import numpy as np
def createDataSet():
group = np.array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]]) #创建 numpy数组 特征值
labels = ['A', 'A', 'B', 'B'] #目标变量
return group, labels
def classify0(inX, dataSet, labels, k):
dataSetSize = dataSet.shape[0] #获得数据集的数目
diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet #inX是分类向量(1X2) 列数为特征数 广播后与数据集相减
sqDiffMat = diffMat ** 2 #每个值平方
sqDistances = sqDiffMat.sum(axis=1) #返回一个List,值是每一行值相加 相当于得到每一个点与需要测试点的距离(还未开根)
distances = sqDistances ** 0.5 #开根
sortedDistIndices = distances.argsort() #返回一个list 值是输入数组的值从小到大的索引 相当于按照距离给值排序
classCount = {}
for i in range(k):
voteIlabel = labels[sortedDistIndices[i]] #取得最近的第i个值
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1 #个数+1
sortdClassCount = sorted(classCount.items(),
key=operator.itemgetter(1), reverse=True) #排序 返回一个List
return sortdClassCount[0][0]
解析数据
假设我们已经有了文本或是其他格式的数据,需要用python解析数据将特征和标签提取出来转为numpy格式.
下面是从文本中提取.格式为1
value value value label
1
2
3
4
5
6
7
8
9
10
11
12
13
14def file2matrix(filename):
fr = open(filename)
arrayOLines = fr.readlines()
numberOfLines = len(arrayOLines)
returnMat = np.zeros((numberOfLines,3)) #3个特征
classLabelVector = []
index = 0
for line in arrayOLines:
line = line.strip()
listFromLine = line.split('\t')
returnMat[index,] = listFromLine[0:3]
classLabelVector.append(int(listFromLine[-1]))
index += 1
return returnMat,classLabelVector
分析数据
利用matplotlib可视化1
2
3
4
5
6scatter = plt.scatter(datingDataMat[:,1],datingDataMat[:,2],15*np.array(labelvector),12*np.array(labelvector))
i, j = scatter.legend_elements()
# print(i, j)
j = ['$\\mathdefault{不受欢迎}$', '$\\mathdefault{受欢迎}$', '$\\mathdefault{一般}$']
ax.legend(i,j,loc='best')
plt.show()
准备数据
归一化
一个样本有多个特征,这些特征的值是不一样的,有些可能一般的值是几十左右,但是其他特征一般的值要高上很大的数量级,但这些特征是等价的.我们需要特征归一化,将取值范围缩小.比如均缩为(0,1)1
newvalue = (oldValue-min)/(max-min)
1
2
3
4
5
6
7
8
9def autonorm(dataSet):
minVals = dataSet.min(0)
maxVals = dataSet.max(0)
ranges = maxVals - minVals
normDataSet = np.zeros(dataSet.shape)
m = dataSet.shape[0]
normDataSet = dataSet - np.tile(minVals,(m,1))
normDataSet = normDataSet/np.tile(ranges,(m,1))
return normDataSet,ranges,minVals
测试算法
评估算法的正确率
将已有数据的一部分用来训练(在KNN这里不需要训练),另一部分用来测试错误率,即这个算法是否优秀1
2
3
4
5
6
7
8
9
10
11
12
13def datingClassTest():
hoRatio = 0.1 #测试数据 10%
datingDataMat,datingLabels = file2matrix('datingTestSet2.txt')
normMat,ranges,minVals = autonorm(datingDataMat)
m = normMat.shape[0]
numTestVecs = int(m*hoRatio)
errorCount = 0.0
for i in range(numTestVecs):
classifierResult = classify0(normMat[i],normMat[numTestVecs:m],datingLabels[numTestVecs:m],3)
print("the classifier came back with:%d,the real answer is %d" %(classifierResult,datingLabels[i]))
if classifierResult!=datingLabels[i]:
errorCount +=1
print("the total error rate is:%f" %(errorCount/float(numTestVecs)))
使用算法
当测试算法后即可直接使用了,输入自己的数据预测1
2
3
4
5
6
7
8
9
10def classifyPerson():
resultList = ['not at all','in small doses','in large doses']
percentTats = float(input("percentage of time spent playing games?"))
ffMiles = float(input("frequent flier miles earned per year?"))
iceCream = float(input("liters of ice cream consumed per year?"))
datingDataMat,datingLabels = file2matrix("./datingTestSet2.txt")
normMat,ranges,minVals = autonorm(datingDataMat)
inArr = np.array([ffMiles,percentTats,iceCream])
classifierResult = classify0((inArr-minVals)/ranges,normMat,datingLabels,3)
print("you will probably look like this person:",resultList[classifierResult-1])
这样一个分类器就实现了.不过比较简单而且是KNN,没有经过算法训练.
手写识别系统
步骤:
- 收集数据 提供文本文件
- 准备数据 编写函数img2vector() 将图像格式转为分类器使用的向量
- 分析数据
- 训练算法,knn不需要
- 测试算法
- 使用算法
手写识别也就是识别图像,而图像的特征可以有很多.
这里识别3232的图像,将每个像素当作特征,也就是一个样本数据是1\1024的向量
首先编写函数3232的二度图转为1\1024的一个样本,特征有1024个1
2
3
4
5
6
7
8def img2vector(filename):
returnVect = np.zeros((1, 1024))
with open(filename, "r+") as f:
for i in range(32):
lineStr = f.readline()
for j in range(32):
returnVect[0, i * 32 + j] = int(lineStr[j])
return returnVect
这样一转化就跟上面一个例子类似了.
然后只要根据已给数据得到特征集和对应label1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26def handwritingClassTest():
hwLabel = []
trainingDataFileList = os.listdir("trainingDigits")
# print(trainingDataFileList)
m = len(trainingDataFileList)
trainingMat = np.zeros((m, 1024)) # 数据集 m个样本 1024个特征
for i in range(m):
fileNameStr = trainingDataFileList[i]
fileStr = fileNameStr.split('.')[0]
classNumStr = fileStr.split('_')[0]
hwLabel.append(int(classNumStr)) #label 目标向量
trainingMat[i, :] = img2vector('trainingDigits/%s' % fileNameStr) #得到每一个样本的特征
testFileList = os.listdir('testDigits')
errorCount = 0
mTest = len(testFileList)
for i in range(mTest): #类似的处理流程 通过得到结果进行比较
fileNameStr = testFileList[i]
fileStr = fileNameStr.split('.')[0]
classNumStr = int(fileNameStr.split('_')[0])
vectorUnderTest = img2vector("testDigits/%s" % fileNameStr)
classifierResult = classify0(vectorUnderTest, trainingMat, hwLabel, 3)
print("the classifier came back with:%d,and the real answer is %s" % (classifierResult, classNumStr))
if classifierResult != classNumStr:
errorCount += 1
print("the total number of errors is %d\n" % errorCount)
print("the total error rate is %f\n" % (errorCount / float(mTest)))
因为特征值都是0或1,在一个量级不需要归一化.
通过上面的KNN学习,可以了解到KNN的时间和空间效率并不高,需要改进.
特点:简单有效,使用算法时必须有接近实际数据的训练样本数据.必须保存全部数据集,必须对每个数据计算距离值,实际使用时可能非常耗时.
决策树
不好意思鸽了这么久
决策树常常是专家经验的概括,是一种分享特定过程知识的方式。例如,在引入可扩展机器学习算法之前,银行业的信用评分任务是由专家解决的,能否放贷是基于一些直观(或经验)的规则,这些规则就可以表示为决策树的形式.它合并一连串逻辑规则,使之成为一个树形的数据结构,这些规则的形式为「特征 a 的值小于 x,特征 b 的值小于 y … => 类别 1」
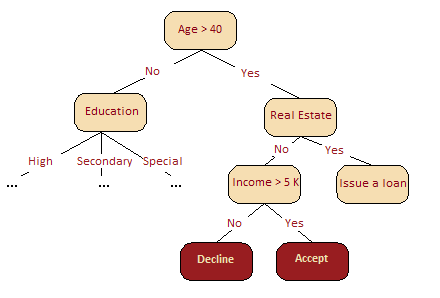
可以简单地发现,决策树可以认为是一种状态图.
根据不同的决策剔除选项.那么如何判断哪些决策能剔除更多的选项呢?
重要概念
熵
熵是一个在物理、信息论和其他领域中广泛应用的重要概念,可以衡量获得的信息量。
对于具有 N 种可能状态的系统而言,熵定义为
其中,$p_i$ 是系统位于第 i 个状态的概率。熵可以描述为系统的混沌程度,熵越高,系统的有序性越差,反之亦然。
信息增益
熵的下降被称为信息增益
对数据进行分组后,对每一组进行熵的计算,再将每组的熵乘以该组所占的比例.得到的就是分组后的熵
所以决策树的构建就很重要.需要避免过拟合的问题.为了避免过拟合,直到熵为某个较小的值。不同的算法使用不同的推断,通过「提前停止」或「截断」以避免构建出过拟合的树.
不同的决策树构建算法依据的指标不一样.
C4.5是信息增益率,ID3是信息增益.同时还有基尼不确定性,$G = 1 - \sum\limits_k (p_k)^2$
错分率 $E = 1 - \max\limits_k p_k$
基尼不确定性和信息增益的效果差不多
二元分类熵的计算
基尼不确定性 1
2
3
4
5
6
7
8
9
10
11
12plt.figure(figsize=(6, 4))
xx = np.linspace(0, 1, 50)
plt.plot(xx, [2 * x * (1-x) for x in xx], label='gini')
plt.plot(xx, [4 * x * (1-x) for x in xx], label='2*gini')
plt.plot(xx, [-x * np.log2(x) - (1-x) * np.log2(1 - x)
for x in xx], label='entropy')
plt.plot(xx, [1 - max(x, 1-x) for x in xx], label='missclass')
plt.plot(xx, [2 - 2 * max(x, 1-x) for x in xx], label='2*missclass')
plt.xlabel('p+')
plt.ylabel('criterion')
plt.title('Criteria of quality as a function of p+ (binary classification)')
plt.legend()
区分不同的标准
附件
1936图灵 自动机理论
自动机有如下基本概念:
符号 :有某种意义或在这个机器上有效的任意数据(datum)。符号有时就叫做“字母”。
字:通过一些符号串接而形成的有限字符串。
字母表 :符号的有限集合。字母表经常指示为Sigma,它是在字母表中所有字母的集合。
语言 :字的集合,由给顶字母表中的符号形成。可以是也可以不是无限的。
学习资料
Cousera吴恩达的机器学习课程
《机器学习实战》python2.x
蓝桥云课程.
