Sekyoro的博客小屋

哈夫曼编/译码

发表于 更新于 分类于
本文字数： 6.7k 阅读时长 ≈ 6 分钟

哈夫曼树

预备知识

1、路径和路径长度

从树中一个结点到另一个结点之间的分支构成两个结点的路径，路径上的分支数目叫做路径长度。树的路径长度是从树根到每一个结点的路径长度之和。

2、带权路径长度

结点的带权路径长度为从该结点到树根之间的路径长度与结点上权的乘积。树的带权路径长度为树中所有叶子结点的带权路径长度之和，通常记作WPL。

若有n个权值为w1,w2,…,wn的结点构成一棵有n个叶子结点的二叉树，则树的带权路径最小的二叉树叫做哈夫曼树或最优二叉树。

哈夫曼树是由n个带权叶子节点构成的所有二叉树中带权路径长度最短的二叉树.

树的带权路径长度

哈夫曼树，又称最优树，是一类带权路径长度最短的树。首先有几个概念需要清楚：

存储结构

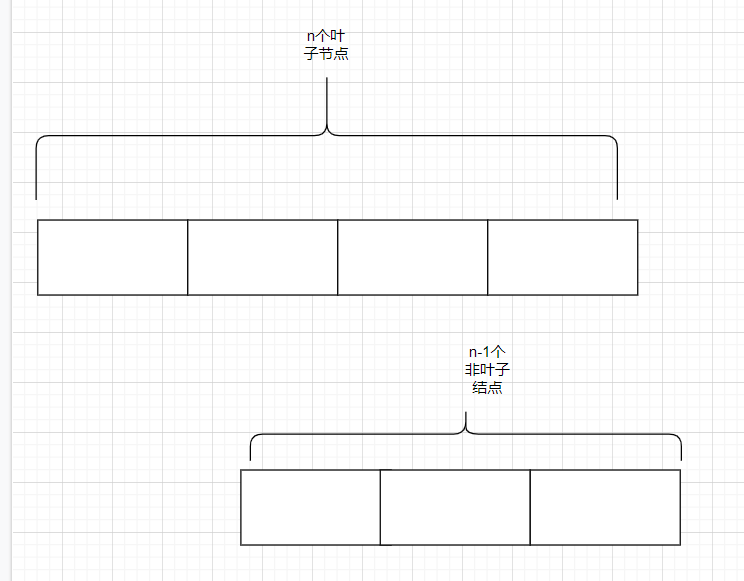
一颗有n个叶子的哈夫曼树共有2n-1个结点，每个结点包含其双亲信息和孩子结点的信息,构成一个静态三链表

2021-5-8

1
2
3
4
5
6
7
8
9
#define N 20
#define M (2*(N)-1)
typedef struct
{
	int weight;//权值
	int parent;//双亲结点
	int Lchild;//左孩子结点
	int rchild;//右孩子结点
}HTNode,HuffmanTree[M+1];

哈夫曼树的存储结构

创建哈夫曼树

1.根据给定的n个权值{w1,w2,…,wn}构成二叉树集合F={T1,T2,…,Tn},其中每棵二叉树Ti中只有一个带权为wi的根结点,其左右子树为空.

2.在F中选取两棵根结点权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的根结点的权值为左右子树根结点的权值之和.

3.在F中删除这两棵树,同时将新的二叉树加入F中.

4.重复2、3,直到F只含有一棵树为止.(得到哈夫曼树)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void CrtHuffmanTree(HufmanTree ht,int w[],int n)
{
		for(int = 1;i<=n;i++)
		ht[i] = {w[i],0,0,0};
		//叶子节点n个
		//初始化每个叶子结点
		m = 2*n-1;
		for(int i = n+1;i<=m;i++)
		ht[i] = {0,0,0,0};
		//初始化n-1个非叶子节点
		
		for(int i = n+1;i<=m;i++)
		{
			select(ht,i-1,&s1,&s2);
			//在叶子节点中选取两个parent=0且weight最小的两个结点
			ht[i].weight = ht[s1].weight+ht[s2].weight;
			ht[s1].parent = ht[s2].parent = i;
			ht[i].lchild = s1;
			ht[i].rchild = s2;			
		}		
}

1、满二叉树不一定是哈夫曼树

2、哈夫曼树中权越大的叶子离根越近 （很好理解，WPL最小的二叉树）

3、具有相同带权结点的哈夫曼树不惟一

4、哈夫曼树的结点的度数为 0 或 2， 没有度为 1 的结点。

5、包含 n 个叶子结点的哈夫曼树中共有 2n – 1 个结点。

6、包含 n 棵树的森林要经过 n–1 次合并才能形成哈夫曼树，共产生 n–1 个新结点

哈夫曼编码

对一颗具有n个叶子的哈夫曼树,若对树中的每个左分支赋予0,右分支赋予1,从根到每个叶子的通路上,各分支的赋值分别构成一个二进制串,该二进制串就称为哈夫曼编码.

QQ截图20210508155705

哈夫曼编码是前缀编码,以使用频度作为权值构造哈夫曼树,这样编码得到的二进制串平均值最短.

（1）创建长度为2n-1的哈夫曼树数组，含有n个叶子节点

（2）创建长度为n的string数组，用于存放n个叶子节点的哈夫曼码

（3）从某叶子节点开始，不断寻找其父节点，直到寻找到根节点，并对此路径上每个分支进行编码，左孩子为0，右孩子为1

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
typedef char* HuffmanCode[N+1];
void CrtHuffmanCode(HuffmanTree ht,HuffmanCode hc,int n)
{
	char *cd;
	cd = (char*)malloc(n*sizeof(char));
	cd[n-1] = '\0';
	for(int i = 1;i<=n;i++)
	{
	start = n-1;
	c = i;
	p = ht[i].parent;//找到叶子结点的父亲节点
	while(p)//如果存在父亲节点.即parent不为0
	{
	--start;
	if(ht[p].lchild==c)
	cd[start] = '0';
	else cd[start] = '1';
	c = p;
	p = ht[p].parent;//继续搜索父亲节点
	}
	hc[i] = (char*)malloc((n-start)*sizeof(char));
	strcpy(hc[i],&cd[start]);
	}
	free(cd);
}

从任意叶子X节点（数组前n项中的某一项）开始，根据X的parent值（即X的父节点在数组中的位置）找到其父节点。

找到X的父节点后，根据父节点的left和right值判断X和父节点的关系。如果X是父节点的左子树，则编码为1；如果X是父节点的右子树，则编码为0。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define N 100
#define M (2 * N - 1)

typedef char *HuffmanCode[N + 1];
typedef struct
{
    int weight; //权值
    int parent; //父节点在ht数组中的位置
    int Lchild; //左孩子在ht数组中的位置
    int Rchild; //右孩子在ht数组中的位置
    char c;     //字符
} HTNode, HuffmanTree[M + 1];

void CrtHuffmanTree(HuffmanTree, int);       //构造哈夫曼树
void select(HuffmanTree, int, int *, int *); //用于寻找最小的两个值
//hc[N+1]为相应节点的编码
void CrtHuffmanCode(HuffmanTree, HuffmanCode, int); //根据哈夫曼树得到相应编码
//解码得到明文
void decode(HuffmanTree, HuffmanCode, int, char *);
//编码得到二进制串
void encode(HuffmanTree, HuffmanCode, int, char *);
//根据HuffmanTree得到HuffmanCode
//HuffmanCode储存的是每个字符对应的编码
int main(void)
{
    int size;
    scanf("%d", &size);
    getchar();
    HuffmanTree ht;
    for (int i = 1; i <= size; i++)
    {
        scanf("%c", &ht[i].c); //输入n个叶子节点的字符
        getchar();
    }
    CrtHuffmanTree(ht, size);
    HuffmanCode hc;
    CrtHuffmanCode(ht, hc, size);
    char encoding_text[100] = {'\0'};
    encode(ht, hc, size, encoding_text);
    decode(ht, hc, size, encoding_text);
    return 0;
}

void CrtHuffmanTree(HuffmanTree ht, int n)
{
    // int w[N + 1];
    // for (int i = 1; i <= n; i++)
    //     scanf("%d", &w[i]); //输入n个叶子节点的权值
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &ht[i].weight); //输入n个叶子节点的权值
        ht[i].parent = ht[i].Rchild = ht[i].Lchild = 0;
    }
    int m = 2 * n - 1;
    for (int i = n + 1; i <= m; i++)
    {
        ht[i].weight = 0;
        ht[i].parent = ht[i].Rchild = ht[i].Lchild = 0;
    }
    int s1, s2; //s1,s2为两个值最小的无父结点
    for (int i = n + 1; i <= m; i++)
    {
        select(ht, i - 1, &s1, &s2);
        ht[i].weight = ht[s1].weight + ht[s2].weight;
        ht[s1].parent = ht[s2].parent = i;
        ht[i].Lchild = s1;
        ht[i].Rchild = s2;
    }
}
void select(HuffmanTree ht, int n, int *s1, int *s2)
{
    int min_1_w = 10000; //用来找最小值
    int min_2_w = 10000; //用来找最小值
    int min;
    for (int i = 1; i <= n; i++)
    {
        if (ht[i].parent == 0)
        {
            if (ht[i].weight < min_1_w)
            {
                min_1_w = ht[i].weight;
                min = i;
            }
        }
    } //找到第一个最小值
    *s1 = min;
    for (int j = 1; j <= n; j++)
    {
        if (ht[j].parent == 0)
        {
            if (j != *s1 && ht[j].weight < min_2_w) //倒数第二小的值大于等于最小的值,小于其余值
            {
                min_2_w = ht[j].weight;
                min = j;
            }
        }
    } //最小的第二个值
    *s2 = min;
}
void CrtHuffmanCode(HuffmanTree ht, HuffmanCode hc, int n) //建立好哈夫曼树后,得到哈夫曼编码
{
    char *cd;                              //cd是指向字符的指针,用来存储字符串
    cd = (char *)malloc(n * sizeof(char)); //开辟n个单元,因为共有n个结点,最多只有n-1个编码位
    cd[n - 1] = '\0';                      //因为存储字符串,最后一位为空字符
    int start, c;                          //start为cd数组开始存储的起点,c用来标记每次往上找到的双亲的位置
    int p;                                 //p为双亲的位置
    for (int i = 1; i <= n; i++)
    {
        start = n - 1;    //这是cd数组的最后一位,是'/0'，因为储存字符串
        c = i;            //c为第一个结点,得到第一个结点的编码
        p = ht[i].parent; //寻找结点父亲
        while (p)         //若有父亲结点
        {
            --start;               //每次递减,从后向前得到编码
            if (ht[p].Lchild == c) //若子节点为左孩子,则为0
                cd[start] = '0';
            else
                cd[start] = '1';
            c = p;
            p = ht[p].parent;
        }
        /*
        while循环可改为
        for(c=i,p=ht[i].parent;p!=0;c=p,p=ht[p].parent)
        {
             --start;
            if (ht[p].Lchild == c)
                cd[start] = '0';
            else
                cd[start] = '1';
            c = p;
        }
        */
        hc[i] = (char *)malloc((n - start) * sizeof(char)); //为hc[i]分配空间,空间大小为编码的位数+1,最后一位为'\0'
        strcpy(hc[i], &cd[start]);                          //注意这里取地址符不可以去掉,因为本身cd是一个数组(指针),但复制时应该从start开始,所以取数组start位的元素地址
                                                            //   printf("%d:%s\n",i,hc[i]);//hc 存储的是n个字符分别的编码
    }
    free(cd);
}
void decode(HuffmanTree ht, HuffmanCode hc, int n, char *encoding_text)
{
    char *text = (char *)malloc(n * sizeof(char));
    memset(text, '\0', sizeof(text));
    int pos = 0;
    int t_pos = 0;
    while (encoding_text[pos] != '\0')
    {
        text[t_pos++] = encoding_text[pos++];
        for (int i = 1; i <= n; i++)
        {
            if (strcmp(text, hc[i])==0)
            {
                printf("%c", ht[i].c);
                memset(text, '\0', n * sizeof(char));
                t_pos = 0;
                break;
            }
            // else
            // {
            //     text[t_pos++] = encoding_text[pos++];

            // }
        }
       // text[t_pos++] = encoding_text[pos++];
    }
    printf("\n");
}
void encode(HuffmanTree ht, HuffmanCode hc, int n, char *encoding_text)
{
    //得到了哈夫曼编码,因为知道了每个字符相应的编码,解码就很简单了
    //进行编码
    getchar();//这里接受一个空格,避免下面fgets直接接受一个空格了
    char text[1000]; //进行编码的文本
    fgets(text, 1000, stdin);
    char c;
    for (int i = 0; text[i] != '\0'; i++)
    {
        c = text[i];
        for (int j = 1; j <= n; j++)
        {
            if (ht[j].c == c)
            {
                printf("%s", hc[j]);
                strcat(encoding_text, hc[j]);
            }
        }
    }
    printf("\n");
}

哈夫曼编码详解——图解真能看了秒懂_Young_IT的博客-CSDN博客

哈夫曼（赫夫曼，哈弗曼）编码算法（带源码+解析） (biancheng.net)

哈夫曼（huffman）树和哈夫曼编码 - dashuai的博客 - 博客园 (cnblogs.com)

-------------本文结束感谢您的阅读-------------
相关文章
感谢阅读.

欢迎关注我的其它发布渠道