稀疏矩阵
1.介绍
概念:矩阵中大多数元素为0。
直观上讲非零元素低于5%。
零元素代表着没有意义的值,所以零元素较多情况下,用链表代替存储比二维数组要好很多。
下面介绍三种表示方法
2.三元组表示
只存储非零元素,由于非零元素位置不存在概率,则利用行,列,值的信息进行存储,这是容易想到的。
随便写个例子(虽然不满足稀疏矩阵定义)
三元组表示法可以写为(假设起始行与列为1)一维数组。
TSMatrix[0],TSMatrix[1],TSMatrix[2]
数组元素为结构体Triple,结构体包含行列与值的信息
三元组表中的元素是有序排列的。(按照行优先、行相同列大小方式)1
2
3
4
5
6
7
8
9
10
11
12
13
typedef struct
{
int i, j; /* 行号和列号 */
ElemType elem; /* 元素值 */
}Triple;
typedef struct
{
Triple data[MaxSize];
int mu, nu, tu; /* 行数、列数和非零元个数*/
}TSMatrix;
这种表示法节省了空间
1.三元组表示法转置
矩阵转置是将行(列)上的元素换到列(行)上
不用三元组表示的话,利用两层for循环,效率O(m*n)
列序递增转置法
采用被转置矩阵三元组表A的列序递增进行转置,这样转置后的矩阵三元组表是以行序递增的。
所以,先以被转置矩阵A的列为主序,内层为每个A矩阵的非零元素1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17Status TransposeSMatrix (TSMatrix M, TSMatrix *T)
{//M为被转置矩阵,T为转置后的矩阵
int p, q, col;
T->mu = M.nu; T->nu = M.mu; T->tu = M.tu;//T的行数为M的列数
if (T->tu){
q = 0;//q可以计数,当转置一个后q+1
for (col = 0; col< M.nu; ++col)
for (p = 0; p< M.tu; ++p)//p为三元组表元素的位置,for循环不断扫描三元组表,查看是否有元素的列数为col,若有则转置
if (M.data[p].j == col) {
T->data[q].i = M.data[p].j;
T->data[q].j = M.data[p].i;
T->data[q].elem = M.data[p].elem;
q++;
}
}
return OK;
}
算法时间效率O(M.nu×M.tu),for两层循环
当矩阵中非零元个数tu和munu同数量级时,则该算法的时间复杂度为O(M.muM.nu2)。因此该算法只适用于M.tu << M.mu*M.nu的情况。
一次定位快速转置法
刚才的算法效率并不是很高,想要提高可以通过减少for循环
如果能预先确定矩阵M中每一列(即T中的每一行)的第一个非零元素在T中的合适位置,那么在对M进行转置时就可以直接放到T中的恰当位置上去。为了确定这些位置,应先求得M的每一列中非零元的个数,进而求得每一列的第一个非零元在T中的位置。(M为被转置矩阵,T为转置后的矩阵)
为了”一次定位”,需要知道
- 待转置矩阵A中的每一列非零元素总数
- A中的每一列第一个非零元素在三元组表中位置
对于第一个,就是转制后矩阵B每一行的非零元个数,设数组num[],则num[col]表示A的第col列非零元素个数;对于第二点,设pos[],pos[col]表示A的第col列第一个非零元在B三元组表的位置。
num[]比较好算,扫一遍三元组表,遇到col值便+1(数组下标法)
pos[]要麻烦一点,它是三元组表中元素的位置,可以通过迭加计算
pos[1] = 1(假设,这里也可以是0,随意了)
pos[col] = pos[col-1] + num[col-1]
具体做法是pos[col]是第col列第一个非零元在三元组表的顺序,当有一个元素加入到B时,则pos[col] = pos[col]+1,使pos[col]始终指向A中第col列中下一个非零元在B的正确存放位置。


如上图1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20Status FastTransposeSMatrix (TSMatrix M, TSMatrix *T)
{ int col, p, q, t;
T->mu = M.nu; T->nu = M.mu; T->tu = M.tu;
if (T->tu) {
for (col=0; col< M.nu; ++col) num[col] = 0;
for (t = 0; t < M.tu; ++t) /*统计每列的非零元个数*/
++num[M.data[t].j];
cpot[0] = 0; /*计算每列第一个非零元转置后的位置*/
for (col = 1; col < M.nu; ++col)
cpot[col] = cpot[col-1] +num[col-1];
for (p = 0; p < M.tu; ++p){
col = M.data[p].j; q = cpot[col];
T->data[q].i =M.data[p].j;
T->data[q].j = M.data[p].i;
T->data[q].elem =M.data[p].elem;
++cpot[col];//当一列有一个元素转置后,位置+1指向下一个该列非零元素
} /* for */
} /* if */
return OK;
}
O(M.nu+M.tu)。
即使非零元个数与munu同数量级,其时间复杂度为O(M.mu M.nu),与经典算法时间复杂度相同
总结
三元组顺序表(有序的双下标法)的特点:
(1)便于进行以行顺序处理的矩阵运算。
(2)若需按行号存取某一行的非零元,需从开始进行查找。
2.三元组表示法加法
1 |
|
3.行逻辑连接的顺序表
由上题快速转置,我们可以想到将pos[]数组放在结构体里,得到行逻辑连接顺序表
概念:为了便于随机存取任意一行的非零元,则需知道每一行的第一个非零元在三元组表中的位置。为此,可将快速转置矩阵的算法中创建的辅助数组cpot,rpos固定在稀疏矩阵的存储结构中。这种带“行链接信息”的三元组表称为行逻辑链接的顺序表。1
2
3
4
5typedef struct{
Triple data[MaxSize];
int rpos[MaxRC+1];//数组起始下标为1
int mu, nu, tu;//分别为行数,列数,非零元个数
}RLSMatrix;
矩阵乘法
以上述结构进行矩阵乘法,可以体现出其优越性
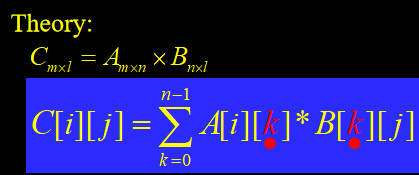
1
2
3
4
5
6
7
8
9C=AxB
for (i=0; i<m; i++)
for (j=0; j<l; j++)
{
C[i][j]=0;
for (k=0; k<n; k++)
C[i][j] += A[i][k]*B[k][j]
}
矩阵的乘法,当两个值其中一个为0,则乘积为0,因此,应免去这种无效操作。
例如矩阵元素(1,2,4)与(2,3,6)则可以算出(1,3,24)
但是若没有相对应的元素(即左乘数的列==右乘数的行),则乘积为0.
因此,只需在右乘数中寻找符合的非零值,利用上述数据结构特点。
rpos[row]为第row行第一个非零元素在三元组表中的位置
基本操作
M×N
对于M中每个元素,找到N中满足条件的值,求的乘积。
矩阵相应位置的值为几个乘积的和,所以设置一个累计和的变量,初值为0.
易忽略点
两个稀疏矩阵相乘的值不一定是稀疏矩阵。
因为几个乘积的和不一定非零,所以算出值后需要检验。
若为0则跳过1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43Status MultiSMatrix(RLSMatrix M, RLSMatrix N, RLSMatrix *Q)
{
int arow, brow, ccol, p, q, t;
float ctemp[];
if (M.mu != N.nu)
return ERROR;
Q->mu = M.mu;
Q->nu = N.nu;
Q->tu = 0;
if (M.tu * N.tu != 0)
{
for (arow = 0; arow < M.mu; ++arow)
{
ctemp[] = 0; //memset(ctemp,0,n*sizeof(float));
Q->rpos[arow] = Q->tu;
for (p = M.rpos[arow]; p < M.rpos[arow + 1]; ++p)
{
brow = M.data[p].j;
for (q = N.rpos[brow]; q < N.rpos[brow + 1]; ++q)
{
ccol = N.data[q].j;
ctemp[ccol] += M.data[p].elem * N.data[q].elem;
} //for q
} // for p
for (ccol = 0; ccol < Q.nu; ++ccol)
{
if (ctemp[ccol] {
if (++Q->tu > MAXSIZE)
return ERROR;
else
{
Q->data[Q->tu].i = arow;
Q->data[Q->tu].j =ccol;
Q->data[Q->tu].elem=ctemp[ccol];
} //else
} //if
} //for ccol
} //for arrow
} //if
return OK;
}
时间复杂度 O(M.mu×N.nu+M.tu×N.tu/N.mu)

4.十字链表
当需要进行矩阵加法,减法,乘法时,矩阵中非零元素个数和位置会发生变化,若用三元组表表示会移动大量元素,相对较麻烦.
十字链表能够灵活插入因运算产生的新的非零元素,删除因运算产生的新的零元素.
由于矩阵有行和列,所以一个结点除了数据域(i, j, elem)之外,还应该用两个方向的指针(right, down),分别指向行和列。这样整个矩阵构成了一个十字交叉的链表,因此称十字链表。每一行或每一列的头指针,可以用两个一维指针数组来存放。1
2
3
4
5
6
7
8
9
10
11
12typedef struct OLNode
{
int i, j;
ElemType elem;
struct OLNode *right, *down;
}OLNode, *OLink;
typedef struct
{
OLink *rHead, *cHead;
int mu, nu, tu;//行数,列数,非零元个数
}CrossList;
初始化十字链表
算法实现
- 读入稀疏矩阵行数列数,非零元个数
- 动态申请行链表,列链表头指针向量
- 逐个读入非零元,分别插入行链表,列链表
1 | Status CreateOLSMatrix (CrossList *M) |
矩阵加法
算法原理
对每一行都用行表头出发分别找到A和B在该行中的第一个非零元,假设非空指针pa和pb分别指向矩阵A和B中行值相同的两个结点,
将B加到A上去时,对A矩阵的十字链表来说,要么改变值(!=0),或者不变(b=0),或者插入一个节点(a=0),或者相加和为0,操作时删除这个节点.
整个运算从从矩阵第一行逐行进行,对每一行都从行表头出发分别找到A和B在该行的第一个非零元节点后开始比较
(1)若pa==NULL或pa->j>pb->j,则需要在A中插入B结点; 欢迎关注我的其它发布渠道
(2)若pa->j==pb->j,且pa->elem+pb->elem!=0,则A结点改值;
(3)若pa->j==pb->j,且pa->elem+pb->elem==0,则需要删除A结点;
(4)若pa->j
为了便于插入和删除结点,需要设立一些辅助指针,比如pre指针指示pa所指结点的前驱结点,每一列也要设立一个指针hl[j],初始值和列链表的头指针相同chead[j]。 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
typedef struct OLNode
{
int i, j, e;
struct OLNode *down, *right;
} OLNode, *OLlink;
typedef struct
{
OLlink *rhead, *chead; //指向行或列第一个非零元(指向结构体的指针),可以用数组rhead[row]表示第row行的数据
int m, n, len; //行列数,非零元个数
} CrossList;
void initial(CrossList *);
void plus(CrossList *, CrossList *);
void print(CrossList *);
void Insert(CrossList *, OLlink, OLlink, OLlink *, OLlink *);
void add(CrossList *, OLlink, OLlink, OLlink *, OLlink *);
int main(void)
{
CrossList *M = (CrossList *)malloc(sizeof(CrossList));
CrossList *N = (CrossList *)malloc(sizeof(CrossList));
scanf("%d %d", &M->m, &M->n);
N->m = M->m;
N->n = M->n;
scanf("%d %d", &M->len, &N->len);
initial(M);
initial(N);
plus(M, N);
print(M);
return 0;
}
void print(CrossList *M)
{
for (int row = 1; row <= M->m; row++)
{
OLlink pa = M->rhead[row];
while (pa)
{
printf("%d %d %d\n", pa->i, pa->j, pa->e);
pa = pa->right;
}
}
}
void plus(CrossList *M, CrossList *N)
{
OLlink pa, pb;
OLlink pre; //指向前面一个节点,方便插入
OLlink *hl = (OLlink *)malloc((M->n + 1) * sizeof(OLlink));
for (int j = 1; j <= M->n; j++)
hl[j] = M->chead[j]; //hl[]表示的是每列非零元的pre指向元素,与pre类似
for (int row = 1; row <= M->m; row++) //行遍历
{
pa = M->rhead[row];
pb = N->rhead[row];
pre = NULL;
while (pb) //当pb有非零元素时进行处理
{
if (pa == NULL || pa->j > pb->j)
{
Insert(M, pa, pb, &pre, hl);
pb = pb->right;
}
else if (pa != NULL && pa->j < pb->j)
{
pre = pa;
pa = pa->right;
}
else if (pa->j == pb->j)
{
add(M, pa, pb, &pre, hl);
pb = pb->right;
}
}
}
}
void add(CrossList *M, OLlink pa, OLlink pb, OLlink *pre, OLlink *hl)
{
int data = pa->e + pb->e;
if (data)
{
pa->e = data;
}
else
{
OLlink temp = (OLlink)malloc(sizeof(OLNode));
if ((*pre) == NULL)
M->rhead[pa->i] = pa->right;
else
{
(*pre)->right = pa->right;
}
temp = pa;
pa = pa->right;
if (M->chead[temp->j] == temp)
M->chead[temp->j] = hl[temp->j] = temp->down;
else
hl[temp->j]->down = temp->down;
free(temp);
}
}
void Insert(CrossList *M, OLlink pa, OLlink pb, OLlink *pre, OLlink *hl) //插入有两种情况,一种是pa该行无非零元素,另一种pb所在列小于pa所在列
{
OLlink p = (OLlink)malloc(sizeof(OLNode));
p->i = pb->i;
p->j = pb->j;
p->e = pb->e;
p->down = p->right = NULL;
if ((*pre) == NULL)
{
M->rhead[p->i] = p;
}
else
{
(*pre)->right = p;
}
p->right = pa;
(*pre) = p;
pa = (*pre)->right;//这一句可以不要
if (!M->chead[p->j] || M->chead[p->j]->i > p->i)
{
p->down = M->chead[p->j];
M->chead[p->j] = p;
}
else
{
p->down = hl[p->j]->down;
hl[p->j]->down = p;
}
hl[p->j] = p;
}
void initial(CrossList *Clist)
{
int i, j, e;
Clist->rhead = (OLlink *)malloc((Clist->m + 1) * sizeof(OLlink));
Clist->chead = (OLlink *)malloc((Clist->n + 1) * sizeof(OLlink));
// if(rhead||chead)
// exit(1);
for (int i = 1; i <= Clist->m; i++)
Clist->rhead[i] = NULL;
for (int i = 1; i <= Clist->n; i++)
Clist->chead[i] = NULL;
OLlink s = (OLlink)malloc(sizeof(OLNode));
for (int count = 0; count < Clist->len; count++)
{
OLlink cur = (OLlink)malloc(sizeof(OLNode));
cur->down = NULL;
cur->right = NULL;
// if(cur==NULL)
// exit(1);
scanf("%d %d %d", &i, &j, &e);
cur->i = i;
cur->j = j;
cur->e = e;
if (Clist->rhead[i] == NULL)
{
Clist->rhead[i] = cur;
}
else
{
s = Clist->rhead[i];
while (s->right != NULL && s->right->j < j)
s = s->right;
cur->right = s->right;
s->right = cur;
}
if (Clist->chead[j] == NULL)
Clist->chead[j] = cur;
else
{
s = Clist->chead[j];
while (s->down != NULL && s->down->i < i)
s = s->down;
cur->down = s->down;
s->down = cur;
}
}
}
